upgrade
Fiveable

♾️AP Calculus AB/BC Unit 9 Review

QR code for AP Calculus AB/BC practice questions

9.2 Second Derivatives of Parametric Equations

♾️AP Calculus AB/BC
Unit 9 Review

9.2 Second Derivatives of Parametric Equations

Written by the Fiveable Content Team • Last updated September 2025
Verified for the 2026 exam
Verified for the 2026 exam•Written by the Fiveable Content Team • Last updated September 2025
♾️AP Calculus AB/BC
Unit & Topic Study Guides
Unit 9 Overview: Parametric Equations, Polar Coordinates, and Vector-Valued Functions
9.1 Defining and Differentiating Parametric Equations
9.2 Second Derivatives of Parametric Equations
9.3 Finding Arc Lengths of Curves Given by Parametric Equations
9.4 Defining and Differentiating Vector-Valued Functions
9.5 Integrating Vector-Valued Functions
9.6 Solving Motion Problems Using Parametric and Vector-Valued Functions
9.7 Defining Polar Coordinates and Differentiating in Polar Form
9.8 Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve
9.9 Finding the Area of the Region Bounded by Two Polar Curves
Pep mascot

9.2 Second Derivatives of Parametric Equations

Refresher time! Recall from 9.1 Defining and Differentiating Parametric Equations the following ideas:

  1. Parametric functions are functions in which independent functions xx and yy are connected via tt, a dummy variable representing time.
  2. To calculate derivatives of parametric equations, dy/dxdy/dx, we first find dy/dtdy/dt (from y(t)y(t)) and dx/dtdx/dt (from x(t)x(t)) and then divide the former by the latter.
  3. Parametric equations are useful in determining the slope of a tangent line at a given point; more broadly speaking, they can inform us about rates of change of physical phenomena like motion.

As point (2) emphasized, we left 9.1 with the toolkit to calculate the first derivative of curves derived parametrically. This section, on the other hand, focuses on computing the second derivative of parametric equations we’ve been describing so far.

Pep mascot
more resources to help you study
practice questionscheatsheetscore calculator

🤔 Finding Second Derivatives of Parametric Equations

Put simply, we denote the second derivative of a parametric function as follows:

d2ydx2\frac{d^2y}{dx^2}

To find said derivative, we’ll use the chain rule: ⛓️

d2ydx2=ddx(dydx)=dy/dtdx/dt=ddtdtdx(dy/dtdx/dt)=ddt(dy/dtdx/dt)dxdt=ddt(dydx)dxdt\frac{d^2y}{dx^2}=\frac{d}{dx}(\frac{dy}{dx})=\frac{dy/dt}{dx/dt}=\frac{d}{dt}\frac{dt}{dx}(\frac{dy/dt}{dx/dt})=\frac{\frac{d}{dt}(\frac{dy/dt}{dx/dt})}{\frac{dx}{dt}}=\boxed{\frac{\frac{d}{dt}(\frac{dy}{dx})}{\frac{dx}{dt}}}

🔨 Breaking Down the Second Derivative

Here's a more in-depth description of the formula above:

Like in any other function, finding the second derivative of a parametric function involves taking the derivative of the first derivative of the function. In order to do this, we first need to find the first derivative of the parametric function, which is known as the parametric derivative as seen in 9.1.

Once we have found the parametric derivative, we can then take the derivative of this equation with respect to the parameter to find the second derivative. This is done by taking the derivative of both sides of the equation with respect to the parameter.

On the left side of the derivation above, the second derivative is denoted as d2ydx2\frac{d^2y}{dx^2}. On the right side, the second derivative is found by taking the derivative of the ratio dydt  /dxdt\frac{dy}{dt} \;/ \frac{dx}{dt} with respect to the parameter.

This can be done using the quotient rule for derivatives, which states that the derivative of a ratio is equal to the difference of the product of the derivative of the numerator and the denominator, and the product of the numerator and the derivative of the denominator, all divided by the square of the denominator.

You might wonder: “The derivation looks so complex!” 😵‍💫 Good news: you don’t need to remember the entire step-by-step process. If you do have the time and energy, it’d be nice learning-wise to be able to derive the second derivative. Otherwise, focus on the last term:

Second Derivative of a Parametric Function: Given any parametric function defined by x(t)x(t) and y(t)y(t), the second derivative is valued at…

ddt(dydx)dxdt\frac{\frac{d}{dt}(\frac{dy}{dx})}{\frac{dx}{dt}}

Like finding first derivatives, calculating second derivatives for parametric equation become more natural with practice. That being said, let’s work out a couple examples!

✏️ Practice Finding Second Derivative of Parametric Functions

We have three questions here for you, with detailed explanations!

🥇 Second Derivative: Example 1

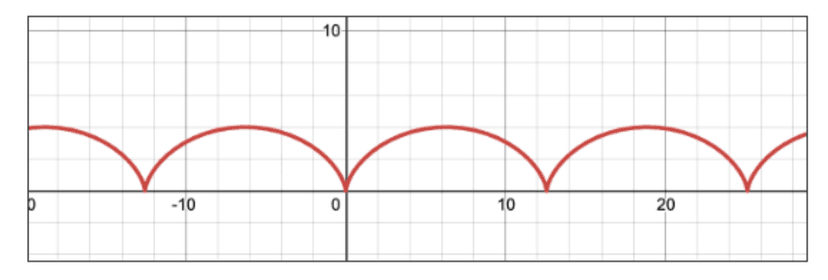
Show that the cycloid defined by x(t)=2(t−sin(t))x(t) = 2(t − sin(t)) and y(t)=2(1−cos(t))y(t)= 2(1 − cos(t)) is concave down on t∈(0,2)t ∈ (0, 2).

💡 Remember: The second derivative gives us information about concavity.

x(t)=2t−2sin(t),y(t)=2−2cos(t)x(t)=2t-2sin(t), y(t)=2-2cos(t)

Finding dx/dtdx/dt and dy/dtdy/dt:

dxdt=2−2cos(t),dydt=2sin(t)\frac{dx}{dt}=2-2cos(t),\frac{dy}{dt}=2sin(t)

Putting these two together to find dy/dxdy/dx, the first derivative:

dydx=2(sin(t))2(1−cos(t))=sin(t)1−cos(t)\frac{dy}{dx}=\frac{2(sin(t))}{2(1-cos(t))}=\frac{sin(t)}{1-cos(t)}

To find the second derivative, we derive dy/dxdy/dx again and divide this derivative by dx/dtdx/dt. The numerator will, thus, look like this after deriving using the quotient rule:

ddt(dydx)=cos(t)(1−cos(t))−(sin(t))(sin(t))(1−cos(t))2\frac{d}{dt}(\frac{dy}{dx})=\frac{cos(t)(1-cos(t))-(sin(t))(sin(t))}{(1-cos(t))^2}

Divide this by dx/dt to get our second derivative… we can further simplify, too!

d2ydx2=cos(t)(1−cos(t))−(sin(t))(sin(t))/(1−cos(t))22(1−cos(t))=cos(t)−cos2(t)−sin2(t)2(1−cos(t))3=...\frac{d^2y}{dx^2}=\frac{{cos(t)(1-cos(t))-(sin(t))(sin(t))}/{(1-cos(t))^2}}{2(1-cos(t))}=\frac{cos(t)-cos^2(t)-sin^2(t)}{2(1-cos(t))^3}=...

Applying the trig identity sin2(t)−cos2(t)=1sin²(t)-cos²(t) = 1:

d2ydx2=...=cos(t)−12(1−cos(t))3=−12(1−cos(t))2\frac{d^2y}{dx^2}=...=\frac{cos(t)-1}{2(1-cos(t))^3}=\frac{-1}{2(1-cos(t))^2}

Since the second derivative is always negative in this equation, the cycloid will always be concave down!

Screenshot 2024-01-22 at 7.24.25 PM.png
Graph displaying the cycloid function and repeatedly shows a concave shape going downward.Courtesy of Desmos

🥈 Second Derivative: Example 2

Consider the parametric equations x=t3−3tx = t³ - 3t and y=t2+2t−5y = t² + 2t - 5. Find the second derivative of yy with respect to xx.

x(t)=t3−3t,y(t)=t2+2t−5x(t)=t^3-3t, y(t)=t^2+2t-5

Finding dx/dtdx/dt and dy/dtdy/dt:

dxdt=3t2−3,dydt=2t+2\frac{dx}{dt}=3t^2-3,\frac{dy}{dt}=2t+2

Putting these two together to find dy/dxdy/dx, the first derivative:

dydx=2(t+1))3(t2−1)=2(t+1)3(t+1)(t−1)=23(t−1)\frac{dy}{dx}=\frac{2(t+1))}{3(t^2-1)}=\frac{2(t+1)}{3(t+1)(t-1)}=\frac{2}{3(t-1)}

Deriving dy/dxdy/dx:

ddt(dydx)=−23(t−1)2\frac{d}{dt}(\frac{dy}{dx})=-\frac{2}{3(t-1)^2}

Divide this by dx/dt to get our second derivative… we can further simplify, too!

d2ydx2=−23(t−1)23(t2−1)=−23(t−1)∗3(t2−1)=−29(t−1)(t2−1)\frac{d^2y}{dx^2}=\frac{\frac{-2}{3(t-1)^2}}{3(t^2-1)}=\frac{-2}{3(t-1)*3(t^2-1)}=\frac{-2}{9(t-1)(t^2-1)}

🥉 Second Derivative: Example 3

A car is moving along a curved road that can be represented by the parametric equations x=t3x = t³ and y=t4y = t⁴. What is the value of the second derivative of yy with respect to xx?

Finding dx/dtdx/dt and dy/dtdy/dt:

dxdt=3t2,dydt=4t3\frac{dx}{dt}=3t^2,\frac{dy}{dt}=4t^3

Putting these two together to find dy/dx, the first derivative:

dydx=4t33t2=43t\frac{dy}{dx}=\frac{4t^3}{3t^2}=\frac{4}{3}t

Deriving dy/dxdy/dx:

ddt(dydx)=43\frac{d}{dt}(\frac{dy}{dx})=\frac{4}{3}

Divide this by dx/dtdx/dt to get our second derivative… we can further simplify, too!

d2ydx2=4/33t2=49t2\frac{d^2y}{dx^2}=\frac{4/3}{3t^2}=\frac{4}{9t^2}

You made it through!

⭐ Closing

Feeling better? Although slightly more convoluted than first derivative calculations, writing down each of the steps helps significantly in making sure you get the right answers at the end. Woo-hoo! 🎈

Vocabulary

The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.

TermDefinition
derivativeThe instantaneous rate of change of a function at a specific point, representing the slope of the tangent line to the function at that point.
parametric functionFunctions where x and y coordinates are each expressed as separate functions of a third variable, typically time (t), rather than y as a function of x.
second derivativeThe derivative of the first derivative, denoted f'', which describes the concavity of a function and indicates where it is concave up or concave down.

Frequently Asked Questions

How do I find the second derivative of parametric equations?

Use the chain-rule recipe from the CED: dy/dx = (dy/dt)/(dx/dt). To get the second derivative, differentiate dy/dx with respect to t, then divide by dx/dt: d2y/dx2 = (d/dt(dy/dx)) / (dx/dt). If you simplify using quotient rule (y' = dy/dt, x' = dx/dt, y'' = d2y/dt2, x'' = d2x/dt2), a convenient formula is d2y/dx2 = (x' y'' − y' x'') / (x')^3. Steps to use on a problem: 1. Compute x', y', x'', y''. 2. Form dy/dx = y'/x' (check x' ≠ 0). 3. Compute d/dt(dy/dx) (or plug into the simplified formula above). 4. Divide by x' to get d2y/dx2. This is exactly CHA-3.G.3 on the AP CED. For practice and a worked example, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try problems at https://library.fiveable.me/practice/ap-calculus.

What's the formula for d²y/dx² when I have parametric functions?

If x = x(t) and y = y(t) with x′(t) ≠ 0, first derivative is dy/dx = (dy/dt)/(dx/dt). The second derivative (d²y/dx²) is found by differentiating dy/dx with respect to t and then dividing by dx/dt (CED CHA-3.G.3): d²y/dx² = (d/dt [ (dy/dt) / (dx/dt) ]) ÷ (dx/dt). A more usable expanded form (quotient + product rules) is d²y/dx² = (x′ y″ − y′ x″) / (x′)³, where primes mean derivatives with respect to t (x′ = dx/dt, x″ = d²x/dt², etc.). Use this to test concavity or find inflection points on a parametric curve; remember dx/dt must be nonzero where you evaluate it. For the AP review, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try practice problems (https://library.fiveable.me/practice/ap-calculus).

I'm so confused about second derivatives with parametric equations - can someone explain the steps?

You're not alone—here's a clear step-by-step you can use every time. 1) Find first derivative: dy/dx = (dy/dt) / (dx/dt). Make sure dx/dt ≠ 0. 2) Differentiate dy/dx with respect to t (use quotient or product + chain rule): d/dt(dy/dx). 3) Divide that result by dx/dt to convert d/dt(dy/dx) into d^2y/dx^2. That gives the standard compact formula: d^2y/dx^2 = (x'(t) y''(t) − y'(t) x''(t)) / (x'(t))^3. Why that works: d^2y/dx^2 = (d/dt(dy/dx)) / (dx/dt). Expanding the numerator with quotient rule yields the expression above. Always check dx'/=0 and be careful with signs. Use d2y/dx2 to test concavity or find inflection points (where it changes sign). This is exactly the CHA-3.G idea on the CED. For a quick walkthrough and examples, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). For more practice problems, try Fiveable’s practice page (https://library.fiveable.me/practice/ap-calculus).

When do I use the formula d²y/dx² = (d/dt(dy/dx))/(dx/dt) instead of just taking the derivative twice?

Use the formula whenever y and x are given as functions of t (parametrically) and you need the second derivative with respect to x. Reason: dy/dx = (dy/dt)/(dx/dt) is a derivative of y with respect to x, but it’s a function of t. To get d^2y/dx^2 you must differentiate that dy/dx with respect to x—which by the chain rule means differentiate dy/dx with respect to t and then divide by dx/dt: 1. Compute dy/dx = (y′(t))/(x′(t)). 2. Compute d/dt[dy/dx]. 3. Divide: d^2y/dx^2 = (d/dt[dy/dx]) / x′(t). Don’t try to get d^2y/dx^2 by naively taking y″(t)/x″(t)—that’s incorrect. Only if you can (and have) solved for y as an explicit function of x (rare for parametrizations) can you differentiate twice with respect to x directly. The parametric formula is what the CED requires (CHA-3.G.3) and is needed for concavity, inflection points, and curvature. For a quick refresher see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). For more practice, check Fiveable’s AP Calc practice problems (https://library.fiveable.me/practice/ap-calculus).

How do I solve parametric second derivative problems step by step?

Step-by-step method you can use every time: 1) Write velocity components: x′(t)=dx/dt and y′(t)=dy/dt. 2) Get first derivative dy/dx = y′(t)/x′(t) (need x′ ≠ 0). This is CHA-3.G. 3) Differentiate that quotient with respect to t: d/dt( y′/x′ ) using the quotient (or product + chain) rule. 4) Divide the result by x′(t) to convert d/dt(dy/dx) into d2y/dx2: d2y/dx2 = [d/dt( y′/x′ )] / x′. 5) A compact formula you’ll often use is useful: d2y/dx2 = (x′ y″ − y′ x″) / (x′)^3, where x″=d2x/dt2 and y″=d2y/dt2. 6) Use this to test concavity (sign of d2y/dx2) or find inflection points (where it changes sign and is defined). Tip: always check x′(t) ≠ 0 and simplify before plugging numbers. This is exactly the AP BC CED skill CHA-3.G. For the study guide and worked examples see the topic page on Fiveable (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). For broader unit review and lots of practice problems, use (https://library.fiveable.me/ap-calculus/unit-9) and (https://library.fiveable.me/practice/ap-calculus).

What's the difference between finding dy/dx and d²y/dx² for parametric equations?

dy/dx for parametric curves gives the slope of the tangent (how y changes with x along the curve). If x = x(t) and y = y(t), dy/dx = (dy/dt) / (dx/dt) (provided dx/dt ≠ 0). d²y/dx² tells you the curve’s concavity—whether the tangent slope is increasing or decreasing as you move along x. You compute it using the CED rule (CHA-3.G.3): d²y/dx² = [d/dt(dy/dx)] / (dx/dt). In practice you differentiate dy/dx with respect to t (use quotient/chain rule) to get d/dt(dy/dx), then divide by dx/dt. Watch out when dx/dt = 0 (vertical tangent)—the formula breaks down there. Physically: dy/dx = slope (direction), while d²y/dx² = concavity (how that direction is changing). For motion problems you’ll also use x″(t), y″(t) (acceleration components) and curvature formulas like κ = |x′y″ − y′x″|/(x′² + y′²)^(3/2). For a step-by-step example and AP-aligned practice see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). More practice questions are at (https://library.fiveable.me/practice/ap-calculus).

Why do I have to divide by dx/dt again when finding the second derivative of parametric functions?

Because the second derivative is the derivative with respect to x of dy/dx, and in parametric form dy/dx is a function of t. So you must change the variable from t back to x using the chain rule. Start with dy/dx = (dy/dt)/(dx/dt). Then d^2y/dx^2 = d/dx(dy/dx) = (d/dt(dy/dx))·(dt/dx). But dt/dx = 1/(dx/dt), so d^2y/dx^2 = [d/dt( (dy/dt)/(dx/dt) )] ÷ (dx/dt). Intuition: d/dt gives the rate of change of the slope as t changes; dividing by dx/dt converts that rate from “per unit t” to “per unit x.” That’s why you differentiate with respect to t once more, then divide by dx/dt. This is exactly the CED result (CHA-3.G.3). For a worked example and practice, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try problems at (https://library.fiveable.me/practice/ap-calculus).

Can someone walk me through how to find d²y/dx² when x = t² and y = t³?

Start by using dy/dx = (dy/dt)/(dx/dt). Here dy/dt = 3t^2 and dx/dt = 2t, so for t ≠ 0 dy/dx = (3t^2)/(2t) = 3t/2. Now differentiate that with respect to t and divide by dx/dt (CED CHA-3.G.3): d/dt(dy/dx) = d/dt(3t/2) = 3/2, dx/dt = 2t. So d²y/dx² = (d/dt(dy/dx)) / (dx/dt) = (3/2) / (2t) = 3/(4t) (for t ≠ 0). Note: at t = 0, dx/dt = 0 so dy/dx and d²y/dx² aren’t defined there (you can’t divide by zero)—check concavity/inflection by considering limits or the parametric curve itself. For more practice on second derivatives of parametric curves see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and plenty of practice problems (https://library.fiveable.me/practice/ap-calculus).

I keep messing up the chain rule when finding second derivatives of parametric equations - what am I doing wrong?

Short answer: you’re probably differentiating dy/dx as if it were with respect to x instead of t—remember the chain rule step for parametrics. Key facts (CED-aligned): - dy/dx = (dy/dt)/(dx/dt). - d2y/dx2 = d/dx(dy/dx) = [d/dt(dy/dx)] / (dx/dt). So compute d/dt(dy/dx) (use quotient rule) and then divide by dx/dt. A common simplified form is d2y/dx2 = (x' y'' − y' x'') / (x')^3, where ' = d/dt. Common mistakes - Differentiating dy/dx with respect to x directly (you must differentiate with respect to t). - Forgetting to divide by dx/dt at the end. - Dropping powers (the denominator ends up cubed). - Sign errors from the quotient rule. Quick checklist when you work one: compute x', y'; compute x'', y''; form y'/x'; compute numerator x' y'' − y' x''; divide by (x')^3. Practice solves it—see the Topic 9.2 study guide for examples (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try more problems at (https://library.fiveable.me/practice/ap-calculus).

How do I know if my parametric curve is concave up or concave down using the second derivative?

Compute dy/dx = y'(t)/x'(t). Then the second derivative is d2y/dx2 = (d/dt (y'/x')) / x' = (x' y'' - y' x'') / (x')^3, provided x'(t) ≠ 0. Interpretation: - If (x' y'' - y' x'')/(x')^3 > 0 on an interval, the curve is concave up there. - If that expression < 0, the curve is concave down. - An inflection point occurs where the expression changes sign (and is defined). Notes for AP BC (CED CHA-3.G): use x', y' for velocity components and x'', y'' for acceleration components. Be careful at times where x'(t)=0 (vertical tangent or cusp): the formula breaks down and you should analyze the curve directly (look at dy/dx limits from either side or parametric sketch). For a short study review, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). For extra practice, try problems at (https://library.fiveable.me/practice/ap-calculus).

What's the process for finding where a parametric curve has inflection points?

Steps to find inflection points for a parametric curve x(t), y(t): 1. Get first derivatives: x′(t)=dx/dt and y′(t)=dy/dt. (You need these for dy/dx.) 2. Compute dy/dx = y′/x′ (only where x′ ≠ 0). 3. Use the CED formula for the second derivative: d2y/dx2 = (d/dt(dy/dx)) / (dx/dt) = (y′′ x′ − y′ x′′) / (x′)³. 4. Solve d2y/dx2 = 0 or where it’s undefined to find candidate t-values. (Both are possible inflection candidates: zero gives concavity change, undefined often signals a vertical tangent or cusp—investigate.) 5. Test each candidate by checking whether d2y/dx2 changes sign as t passes through the candidate (or examine concavity of y vs x). If sign changes, the corresponding point (x(t), y(t)) is an inflection point. 6. Make sure the curve is defined there and note any special behavior (vertical tangents, cusps). This procedure matches AP requirement CHA-3.G.3 (compute d2y/dx2 via d/dt(dy/dx) divided by dx/dt). For more examples and practice, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and thousands of practice problems (https://library.fiveable.me/practice/ap-calculus).

I missed class on parametric second derivatives and I'm completely lost - where do I even start?

Start with dy/dx = (dy/dt) / (dx/dt). To get the second derivative with respect to x use the CED formula: d2y/dx2 = [ d/dt (dy/dx) ] / (dx/dt). Work it out with primes (′ = d/dt): 1) dy/dx = y′/x′. 2) d/dt(dy/dx) = (y″ x′ − y′ x″) / (x′)2 (quotient rule). 3) Divide by x′: d2y/dx2 = (y″ x′ − y′ x″) / (x′)3. That last expression is often the fastest to use: plug x′, y′, x″, y″ (velocity and acceleration components). Sign of d2y/dx2 tells concavity of the parametric curve; zeros where it changes sign are potential inflection points. For curvature you’ll see a related numerator |x′ y″ − y′ x″| and a (x′2 + y′2)3/2 denominator. If you want practice, the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) has worked examples, and Fiveable’s unit page (https://library.fiveable.me/ap-calculus/unit-9) and practice bank (https://library.fiveable.me/practice/ap-calculus) have lots of problems to try.

Do I need to simplify d²y/dx² or can I leave it as a fraction with t in it?

You don’t have to eliminate t. For parametric curves the AP CED (CHA-3.G.3) expects you to compute d2y/dx2 = (d/dt(dy/dx)) / (dx/dt), so the second derivative will normally be an expression in t. Leaving d2y/dx2 as a fraction with t in it is fine—in fact that’s the standard answer on the exam unless the problem explicitly asks for concavity or an inflection point in terms of x or asks you to evaluate at a specific t (then you plug in the t-value). Two important caveats: - Always watch for dx/dt = 0 (division by zero) and say what that means for the formula or the curve’s vertical tangent. - If the question asks for concavity on an x-interval, or for d2y/dx2 at a specific x, you’ll need to relate t to x (solve for t or give the t-interval that corresponds). For a refresher and worked examples on this exact topic, check the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq). For extra practice, use Fiveable’s AP Calc practice set (https://library.fiveable.me/practice/ap-calculus).

How do I find the second derivative when both x(t) and y(t) are trig functions?

Use the parametric second-derivative formula from the CED: d2y/dx2 = (d/dt(dy/dx)) / (dx/dt). Steps when x(t) and y(t) are trig: 1. Compute x′(t) and y′(t). 2. Form dy/dx = y′(t)/x′(t). 3. Differentiate that expression with respect to t (use quotient or product + chain rules). 4. Divide the result by x′(t). Quick example: x(t)=cos t, y(t)=sin t. - x′ = −sin t, y′ = cos t so dy/dx = cos t/(−sin t) = −cot t. - d/dt(dy/dx) = d/dt(−cot t) = csc^2 t. - d2y/dx2 = (csc^2 t) / (−sin t) = −csc^3 t. Keep an eye on where x′(t)=0 (vertical tangents)—the formula breaks there. This is exactly CHA-3.G.3 territory in the AP CED. For a short review and more examples, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try practice problems at (https://library.fiveable.me/practice/ap-calculus).

Why does my calculator give me a different answer when I try to find d²y/dx² for parametric equations?

Your calculator is probably differentiating with respect to t (giving d²y/dt²) or using a different internal variable—but the AP formula you need is in terms of x as the independent variable. For parametrics: dy/dx = (dy/dt) / (dx/dt). Then the second derivative (concavity of y vs x) is d²y/dx² = [d/dt(dy/dx)] ÷ (dx/dt). So on your calculator you must: (1) compute dy/dx as a function of t, (2) differentiate that result with respect to t, and (3) divide by dx/dt. If you instead ask the calculator for d²y/dt² or accidentally differentiate dy/dx with respect to x, you’ll get the “different” answer. Also watch out for points where dx/dt = 0 (vertical tangent)—the formula breaks there. Example: x=t², y=t³. dy/dx = (3t²)/(2t) = 3t/2. d/dt(dy/dx)=3/2. dx/dt=2t. So d²y/dx² = (3/2)/(2t) = 3/(4t). That’s the value the AP CED expects (use CHA-3.G.3). For more explanation and AP-style practice, see the Topic 9.2 study guide (https://library.fiveable.me/ap-calculus/unit-9/second-derivatives-parametric-equations/study-guide/3lZ6t0UnfoooCAKbZ3Hq) and try problems on Fiveable’s practice page (https://library.fiveable.me/practice/ap-calculus).