7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
Welcome to topic 7.7, where you’ll learn about how to find unique solutions to differential equations. You’ve almost made it to the end of the unit! 🌟
In this topic, we’ll learn about the difference between a general solution and a particular solution using separation of variables. To review separation of variables, please look at 7.6 linked here!

🤔 Difference Between General and Particular Solutions
A general solution to a differential equation consists of a constant in the equation. Therefore, when you change the constant, you can get multiple equations when plotting, as seen in the picture below on the left side below. ⬅️ You get a general solution when you don’t have any initial conditions that are given by the problem. When plotting the general solution, you will also get a graph that looks similar to a slope field. For references on slope fields, please look at 7.3 and 7.4!
However, when given an initial condition in the problem, you can solve for a specific equation, which leaves you with one equation on your graph, like on the right side below. ➡️
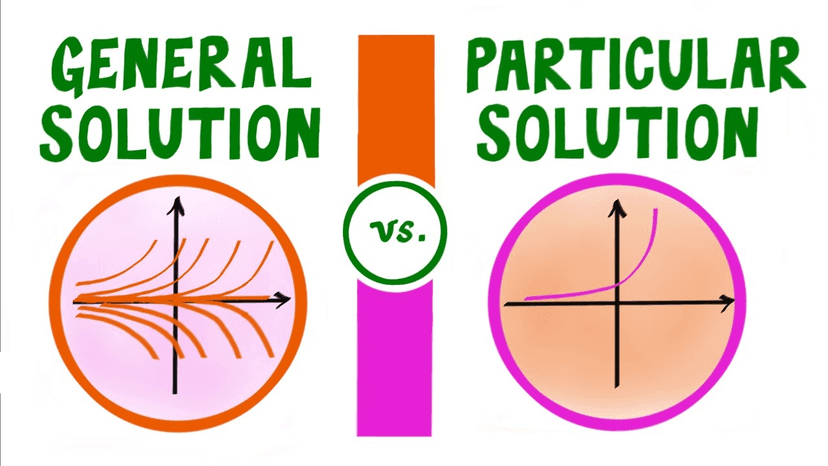
Essentially…
- 🎩 A general solution to a differential equation is a family of functions that satisfies the equation. There are infinitely many functions that could do so!
- 🎯 A particular solution is a unique solution that passes through a specific point, and we can calculate it when given initial conditions.
🧠 Particular Solution Function
When this topic shows up on free-response questions and you’re asked to write an expression, you must include the initial condition. Here is a general form that you can use:
This is a particular solution to the differential equation , where (the initial condition!).
Now, let’s get into how to do the math behind finding a particular solution.
🪜 Steps for Solving a Separation of Variables Problem with Initial Conditions
Here are some steps you can follow!
- 🪓 Separate the two variables that you will be using. For example, gather all the ’s on one side and ’s on the other side.
- ◀️ Integrate both sides of the equation with respect to their variables. Make sure not to forget to add the !
- 🟰 Solve for to get the general equation.
- 1️⃣ Plug in your initial conditions (which are given!) for and and solve for .
- 🟰 Finally, plug back in your that you calculated and there’s your particular solution!
This skill combines a lot of skills you already practiced! ✏️
😑 Consideration: Domain Restrictions
Solutions to differential equations may not always be defined for all values of the independent variable. There may be restrictions on the domain, or range of values, for which the solution is valid. These restrictions can arise for several reasons, including:
-
Singularities - Certain values of the independent variable may result in division by zero or other mathematical singularities in the solution, leading to an undefined solution.
-
Physical constraints - The solution may only be physically meaningful within certain ranges of the independent variable. For example, the position of a projectile may only be defined when it is above the ground, and not when it is below.
-
Mathematical constraints - Certain mathematical conditions may be required for the solution to be well-defined. For example, the solution may only be valid for positive values of the independent variable.
It's important to keep these domain restrictions in mind when solving differential equations and interpreting the results. Ignoring the domain restrictions can lead to incorrect or meaningless solutions. To avoid this, it may be necessary to split the domain into several intervals, each with its own solution, or to use different methods to obtain a solution for different parts of the domain.
Imagine you were asked to find the particular solution of the following differential equation, given the initial condition .
We can see here that there is a domain restriction since the denominator becomes zero when . Therefore, the solution cannot include these values.
📝 AP Free-Response Practice Problem
The following free-response question (FRQ) is from the 2012 AP Calculus AB examination administered by College Board. All credit goes to College Board. We are only going to work on part c since it is the part that focuses on solving differential equations with an initial condition!
The rate at which a baby bird gains weight is proportional to the difference between its adult weight and its current weight. At time , when the bird is first weighed, its weight is 20 grams. If is the weight of the bird, in grams, at time $t$ days after it is first weighed, then
Let be the solution to the differential equation above with initial condition .
(c) Use separation of variables to find , the particular solution to the differential equation with initial condition .
Let’s follow the steps we outlined before!
🪓 Step 1: Gather all the ’s on one side and ’s on the other side.
Another possible separation could be moving the to the left side and leaving 1 on the right side!
◀️ Step 2: Integrate both sides of the equation with respect to and .
🟰 Step 3: Add the $+C$ and solve for the general equation!
Note that this consists of the constant from integrating the left side plus the constant from integrating the right side! Since it is a constant, we can always redefine for the situation!
💡 If you ever forget if you have to differentiate or integrate, remember that separate rhymes with integrate more than differentiate!
1️⃣ Step 4) The initial conditions for this problem are for and . Solve for algebraically.
We eliminated the absolute value sign on the left side of the equation because according to the graph that was provided, all the values for were positive for !
🟰 Step 5: Plug back in and solve for !
You already know how to do everything up to step 4 and everything after step 4 is just algebra and arithmetic! You’ve got this with practice! 😃
🔢 Scoring Guidelines Tips
Typically on an FRQ, if there is a differential equation problem, the bulk of the points will come from the part about the differential equation. Here are some important tips to make sure you maximize your points!
1️⃣ Always separate your variables.
Even if you don’t know how to integrate, simply separating your variables can get you one point on the part! If you don’t separate your variables, you lose all the points for that part of the question, even if you do something right later on.
2️⃣ Never forget the .
The constant of integration is incredibly important in differential equation problems because that is how you can use the initial condition to narrow a general solution to a particular solution.
The maximum number of points you can get without the constant is 2: one for separation and one for finding the correct antiderivatives.
📕 Closing
Initially, these types of differential equations will be hard, but with practice and the explicit step-by-step procedure, you can totally rock those questions in the free-response section! You’ve got this! 👏
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| differential equation | An equation that relates a function to its derivatives, describing how a quantity changes in relation to one or more variables. |
| domain restrictions | Limitations on the set of input values for which a solution to a differential equation is valid or defined. |
| general solution | The complete family of solutions to a differential equation, containing arbitrary constants that represent all possible particular solutions. |
| initial condition | Specified values of a function at particular points that determine which particular solution to a differential equation is selected. |
| particular solution | A specific solution to a differential equation obtained by using initial conditions to determine the values of arbitrary constants. |
Frequently Asked Questions
How do I find a particular solution to a differential equation when I have an initial condition?
Find the general solution, then use the initial condition to pin down the constant. Two common cases: - If dy/dx = f(x) (only x), integrate: y = ∫ f(x) dx + C. Use the initial condition y(a)=y0 to get C = y0 − ∫_a^? f(x) dx (or use the definite-integral form F(x)=y0+∫_a^x f(t) dt per FUN-7.E.2). - If the equation is separable, dy/dx = g(x)h(y), separate and integrate: ∫ (1/h(y)) dy = ∫ g(x) dx + C. Solve (implicitly or explicitly) for y, then substitute the given point y(a)=y0 to find C. Always check domain restrictions (FUN-7.E.3) and whether you can solve explicitly. Existence/uniqueness tells you there’s exactly one particular solution through the point when conditions hold. For step-by-step examples and practice, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7). For lots of extra problems, check Fiveable practice (https://library.fiveable.me/practice/ap-calculus).
What's the difference between a general solution and a particular solution for differential equations?
A general solution of a differential equation is the family of all solutions you get after integrating—it includes an arbitrary constant (or constants) and represents infinitely many curves. A particular solution is one specific member of that family found by applying an initial condition (e.g., y(a)=y0) to solve for the constant(s). So the general solution + an initial condition = the unique particular solution that passes through the given point (FUN-7.E.1, FUN-7.E.2). Remember to check domain restrictions: solutions may only be valid on intervals where the function and integrals are defined (FUN-7.E.3). For practice with separation of variables and initial-value problems, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and more problems at the Unit 7 page (https://library.fiveable.me/ap-calculus/unit-7) or the practice bank (https://library.fiveable.me/practice/ap-calculus).
When do I use separation of variables vs just integrating both sides?
Use plain integration when the DE is already in the form dy/dx = f(x). Then a particular solution through (a, y0) is F(x) = y0 + ∫_a^x f(t) dt (FUN-7.E.2)—you don’t need to separate variables because the right side depends only on x. Use separation of variables when the derivative factors into a function of y times a function of x, i.e. dy/dx = g(x)·h(y). Then rearrange to isolate y’s with dy and x’s with dx: (1/h(y)) dy = g(x) dx, integrate both sides, and use the initial condition to find the constant. You may end up with an implicit solution; solve explicitly if possible and check domain restrictions (FUN-7.E.3). Always apply the initial condition to get the unique particular solution (FUN-7.E.1) and be mindful of existence/uniqueness on the domain. For worked examples and AP-style practice, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and the Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7). You can practice more DE problems at (https://library.fiveable.me/practice/ap-calculus).
How do I solve dy/dx = f(x) step by step with an initial condition?
If dy/dx = f(x) and you’re given an initial condition y(a) = y0, here’s the step-by-step (CED-aligned): 1. Recognize this is separable/simple: dy/dx = f(x) depends only on x. 2. Integrate both sides with respect to x: ∫ dy/dx dx = ∫ f(x) dx ⇒ y = F(x) + C, where F is any antiderivative of f. (This is the general solution.) 3. Use the initial condition y(a)=y0 to find C: y0 = F(a) + C ⇒ C = y0 − F(a). 4. Write the particular solution: y(x) = F(x) + y0 − F(a). Equivalently (FUN-7.E.2), y(x) = y0 + ∫_a^x f(t) dt. That formula automatically satisfies y(a)=y0. 5. Check domain restrictions: make sure f and F are defined on an interval containing a (CED: FUN-7.E.3). Note the existence/uniqueness theorem assures one particular solution through the given point when f is continuous. For extra practice and AP-style examples, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy), the whole Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7), and tons of practice problems (https://library.fiveable.me/practice/ap-calculus).
I'm confused about why F(x) = y₀ + ∫f(t)dt from a to x - can someone explain this formula?
Think of solving dy/dx = f(x) with the initial condition y(a) = y0. When you integrate f(x) you get an antiderivative plus a constant: y = F(x) = A(x) + C. Writing the solution as F(x) = y0 + ∫_a^x f(t) dt builds that constant into the integral so the initial condition is satisfied automatically. Why it works (two facts from the CED / Fundamental Theorem of Calculus): - Differentiation: d/dx [y0 + ∫_a^x f(t) dt] = f(x). So F′(x) = f(x), meaning F solves the differential equation (FUN-7.E.2). - Initial value: at x = a, F(a) = y0 + ∫_a^a f(t) dt = y0. So it’s the unique particular solution through (a, y0). Practical note: using the definite integral avoids juggling the “+C” explicitly and makes domain issues clearer—check where f is continuous to ensure existence/uniqueness. For more practice and CED-aligned examples see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and the Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7). For extra problems try the AP practice bank (https://library.fiveable.me/practice/ap-calculus).
What does it mean when a differential equation solution has domain restrictions?
A solution having domain restrictions means the particular function you found only solves the differential equation on some interval(s) of x—not necessarily for all real x. That happens for reasons covered in the CED (FUN-7.E.3): you may introduce a division by zero or a logarithm when separating variables, the differential equation may be undefined at certain points, or an initial condition picks one branch of an implicit solution. For example, separating dy/dx = y/x gives ln|y| = ln|x| + C, so solutions like y = Cx exclude x = 0 (and you must pick sign/branch). Existence and uniqueness also guarantee a unique particular solution only on an interval where f and ∂f/∂y are continuous around the initial point. On the AP exam, always state the interval where your solution is valid and check singular points. For a refresher, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and unit overview (https://library.fiveable.me/ap-calculus/unit-7). For more practice, try problems at https://library.fiveable.me/practice/ap-calculus.
How do I know if I can separate variables in a differential equation?
You can separate variables when you can rewrite the differential equation so all x terms (and dx) are on one side and all y terms (and dy) are on the other—i.e. it becomes dy/dx = g(x)·h(y) so (1/h(y)) dy = g(x) dx. Quick checklist: - Try to algebraically rearrange: move factors so y-terms multiply dy and x-terms multiply dx. - If y appears only in a factor that can be isolated (e.g. (y^2+1) or y on numerator/denominator), it’s separable. - If x and y are mixed (e.g. y + x*y or y as a sum with x inside a nonfactorable expression) and you can’t factor into g(x)h(y), it’s not separable—consider integrating factor or other methods. - Don’t forget constant/implicit solutions like y = 0 that might be lost when dividing by h(y). Check domain restrictions and include initial conditions to solve for the integration constant (CED FUN-7.E.1–3). Separable steps: separate → integrate both sides → solve for y (explicit if possible) → apply initial condition to find C → state domain. For the AP topic overview and worked examples, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy). For more practice, use the unit page (https://library.fiveable.me/ap-calculus/unit-7) and the practice problem bank (https://library.fiveable.me/practice/ap-calculus).
Can you walk me through finding a particular solution using initial conditions from start to finish?
Start with the differential equation and the initial condition (an initial value problem). Steps for separation-of-variables IVPs: 1. Separate variables: rewrite so all y terms with dy on one side and x terms with dx on the other, e.g. dy/g(y) = f(x) dx. 2. Integrate both sides: ∫ dy/g(y) = ∫ f(x) dx. Put a +C on one side to get the general (implicit) solution. 3. Solve for y explicitly if possible. 4. Use the initial condition (x0, y0) to substitute into the general solution and solve for C—that gives the unique particular solution (FUN-7.E.1, FUN-7.E.2). 5. State any domain restrictions from where the algebra/integrals are valid and check existence/uniqueness (e.g., continuity of f and ∂f/∂y). Quick example: dy/dx = 3y, y(0)=2. Separate: dy/y = 3 dx → ln|y| = 3x + C → y = Ce^{3x}. Use y(0)=2 → C=2 so y = 2e^{3x}. For more on Topic 7.7 see the Fiveable study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy). For extra practice, try problems at (https://library.fiveable.me/practice/ap-calculus).
Why does a general solution have infinitely many solutions but a particular solution is just one?
A general solution includes an arbitrary constant because when you integrate dy/dx = f(x) you get y = F(x) + C—every different C gives a different curve that still satisfies the differential equation, so there are infinitely many solutions. A particular solution is the single one you get after using an initial condition (an (x0, y0) point) to determine C. For example, if y = F(x) + C and you know y(x0) = y0, plug in to solve C = y0 − F(x0); that fixes the constant and gives the unique particular solution that passes through that point. This is exactly FUN-7.E in the CED: one general family (infinitely many) vs. one particular curve through a specified point; you can also see the definite-integral form F(x) = y0 + ∫_a^x f(t) dt which constructs the particular solution directly. For extra review and practice on this topic, check the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7).
When I separate variables do I always add the constant of integration to both sides?
Short answer: no—you don’t have to write a “+C” on both sides, but you must account for one arbitrary constant. Why: when you integrate both sides after separating variables you get two antiderivatives that differ by a constant. Writing ∫g(y) dy = ∫f(x) dx + C or G(y) = F(x) + C is enough because any constant of integration on the left can be moved into a single constant on the right (they combine into one arbitrary constant). Then use the initial condition to solve for that single constant and get the particular solution (FUN-7.E.1 and FUN-7.E.2). Extra points for AP problems: note domain restrictions (where separation/inversion is valid) and check existence/uniqueness if needed (CED). For a quick refresher on examples and steps, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy). For extra practice, try problems at (https://library.fiveable.me/practice/ap-calculus).
How do I use an initial condition like y(0) = 3 to find the value of C in my general solution?
When you have a general solution that includes an arbitrary constant C, use the initial condition by plugging the given x and y into that solution and solving algebraically for C. Steps: 1. Write the general solution y = G(x, C) you found (explicit or implicit). 2. Substitute x = 0 and y = 3 into G. That gives an equation in C only. 3. Solve that equation for C. Substitute that value back to get the particular solution. Quick examples: - If your general solution is y = Ce^{2x} and y(0)=3, plug in: 3 = C e^{0} → C = 3, so y = 3e^{2x}. - If the implicit solution is ln|y| = x + C and y(0)=3, plug in: ln 3 = 0 + C → C = ln 3, so ln|y| = x + ln 3 (or y = 3e^x). Remember domain restrictions (FUN-7.E.3)—the initial point must lie in the solution’s domain—and that a unique particular solution passes through the given point (FUN-7.E.1). For more on using initial conditions and separation of variables, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy). For extra practice, check the unit page (https://library.fiveable.me/ap-calculus/unit-7) and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).
I don't understand when separation of variables works - what types of differential equations can I use it for?
Separation of variables works exactly for differential equations you can write as dy/dx = g(x)·h(y)—i.e., the x-part and y-part factor into a product. If you can rearrange to 1/h(y) dy = g(x) dx, you integrate both sides to get an implicit general solution, then use the initial condition to solve for the constant and get the particular solution (this is the FUN-7.E idea). Notes you should remember: - You may get an implicit solution; sometimes you can solve for y explicitly. - Domain restrictions matter: h(y) = 0 can give constant (equilibrium) solutions or block dividing by h(y); check where your manipulations are valid. - Existence/uniqueness: if h and g are continuous and h(y0) ≠ 0 at the initial point, you usually have a unique local solution. - If the equation isn’t separable, use other methods (integrating factor for linear first-order, etc.). For a focused review of examples and AP-style practice, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy), the Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7), and more practice problems (https://library.fiveable.me/practice/ap-calculus).
What's the step by step process for solving dy/dx = xy with separation of variables?
1) Recognize it's separable: dy/dx = x y. Rewrite as dy/y = x dx (y ≠ 0). 2) Integrate both sides: ∫(1/y) dy = ∫ x dx → ln|y| = x^2/2 + C. (constant of integration) 3) Solve for y explicitly: |y| = e^{x^2/2 + C} = e^C e^{x^2/2}. Let A = ±e^C, so y = A e^{x^2/2} (general solution). 4) Use an initial condition y(x0)=y0 to find A: y0 = A e^{x0^2/2} ⇒ A = y0 e^{-x0^2/2}. Substitute back to get the particular solution y = y0 e^{(x^2 - x0^2)/2}. 5) Note domain restrictions: because of ln|y| you must check if y can be 0; y≡0 is also a valid solution. Also specify interval containing x0 for uniqueness (CED FUN-7.E, existence/uniqueness). For more AP-style practice and reminders about initial conditions and domain, see the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy) and the Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7).
How do I handle domain restrictions when solving differential equations with initial conditions?
When you find a particular solution, always check where the formula you solved is actually valid—that’s the domain restriction idea in FUN-7.E.1–7.E.3. Quick checklist: - Solve the DE (by separation or antiderivative) and get the general solution with a constant C. Watch for algebra that forced you to divide by something (e.g., dividing by y or by an expression in x)—those values are excluded from the solution’s domain. - Use the initial condition to pick C, but make sure the initial point lies in a region where the general solution is defined. If it doesn’t, either a different branch or a singular solution (like y = 0) might apply. - If you used ln or arcsin, remember their argument restrictions (ln > 0, |arg| ≤ 1 for arcsin)—that restricts x or y values. - State the maximal interval containing the initial x where the solution is valid (this ties to existence/uniqueness ideas on the AP). On the exam, always state domain restrictions and justify them. For practice, check the Topic 7.7 study guide (https://library.fiveable.me/ap-calculus/unit-7/finding-particular-solutions-using-initial-conditions-separation-variables/study-guide/v0tgJcQJwgznHGMkq2Uy), the Unit 7 overview (https://library.fiveable.me/ap-calculus/unit-7), and try problems from the AP practice pool (https://library.fiveable.me/practice/ap-calculus).