5.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points
Welcome back to AP Calculus with Fiveable! This topic focuses on extrema in an interval. Let’s dive right into the world of extreme values, both global and local, and the crucial concept of critical points. 🙌

🎢 Extreme Value Theorem
Let's start with the Extreme Value Theorem. The College Board AP Calculus Exam description states that a function defined on a closed interval must have both a maximum and minimum value within that interval. This is known as the Extreme Value Theorem, and it holds true if the function is continuous over the given interval . Check out this Fiveable guide to review continuity: Confirming Continuity over an Interval.
Check out the graph below. On the interval , there is one minimum value at , another at , and a maximum value at some point between and . It is okay for the minimum or maximum value to be at an end point, in fact, is is expected and something we need to check for!
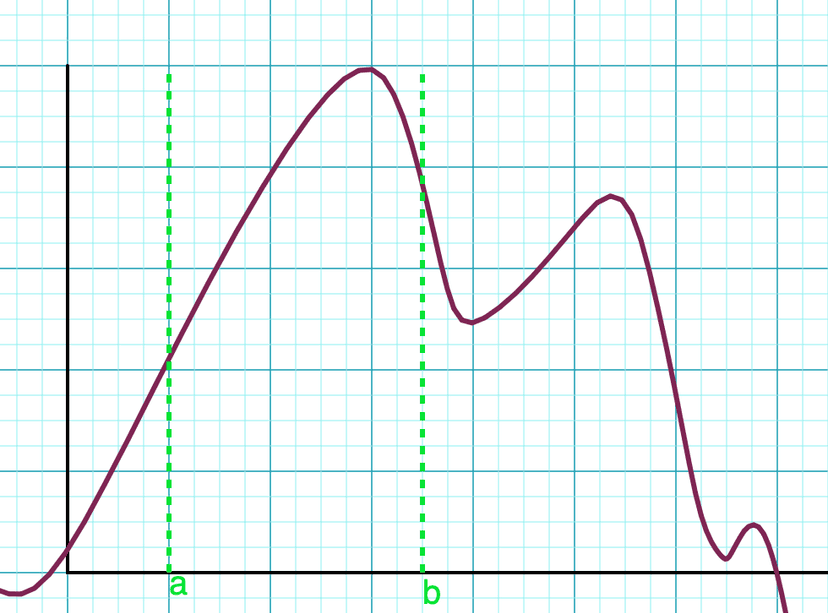
Graph of function with max and min value
Graph created with Virtual Graph Paper
To apply this theorem effectively, think of the function as a roller coaster. As long as the roller coaster is continuous without any breaks or disruptions (discontinuities), you can expect it to have both a highest peak (maximum) and a lowest dip (minimum) somewhere along the ride. 🎢
🌐 Global Versus Local Extrema
Now, let's explore the difference between global and local extrema. Global extrema are the absolute maximum and minimum values of a function over its entire domain. We can identify these points because they are the absolute highest or lowest points when considering the function as a whole.
📍 Local extrema, on the other hand, focus on specific regions or intervals within the function. These points might not be the absolute highest or lowest in the entire domain but are the peaks and valleys within localized sections. We can identify these points if they are a maximum or minimum relative to the values directly surrounding them.
Take a look at this image below and try to identify all extrema as local or absolute and maximums or minimums on the interval .
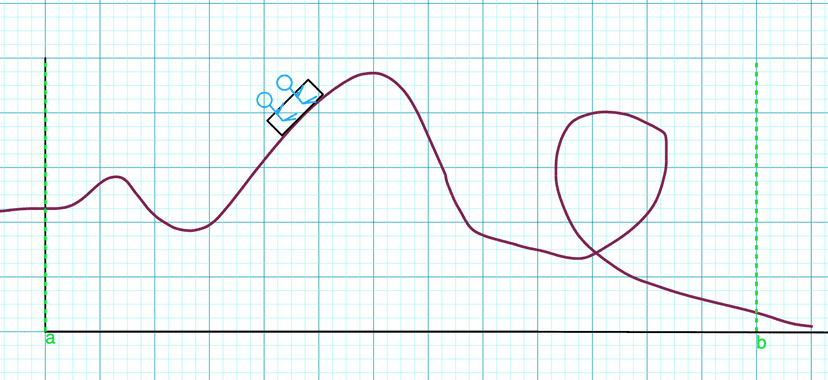
Using the Extreme Value Theorem, we can conclude that there must be one absolute maximum and one absolute minimum value on the interval since the function is continuous at all points.
Additionally, there are a few other points that qualify as local extrema because they are higher or lower than the points surrounding them. Consider if those points would also qualify as global extrema.
Let’s check that our points match with the ones marked below:
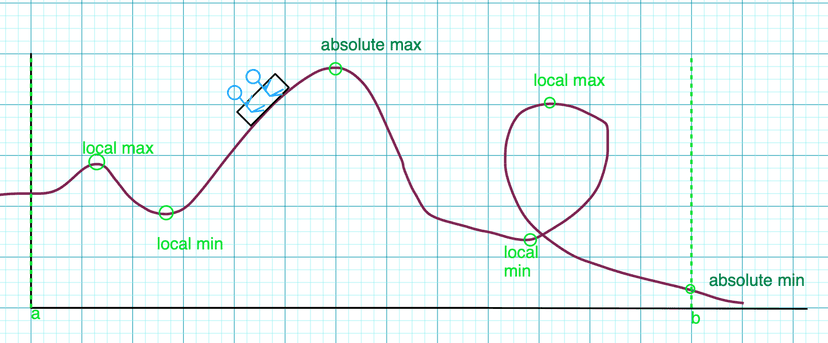
Great work!👍
🎯 Critical Points
Critical points play a pivotal role in identifying where extrema can occur. A critical point is a value in the domain of a function where the function is either not differentiable or its derivative is equal to zero: .
Think of critical points as potential tipping points on our roller coaster. At these points, the roller coaster may momentarily pause, change direction, or even come to a standstill. These critical points become the candidates for both local maxima and minima.
Look at the graph below. All of its extrema are critical points, but not all critical points are extrema! Point is a critical point since the derivative of the function at is 0, but it is not a local maximum or minimum.
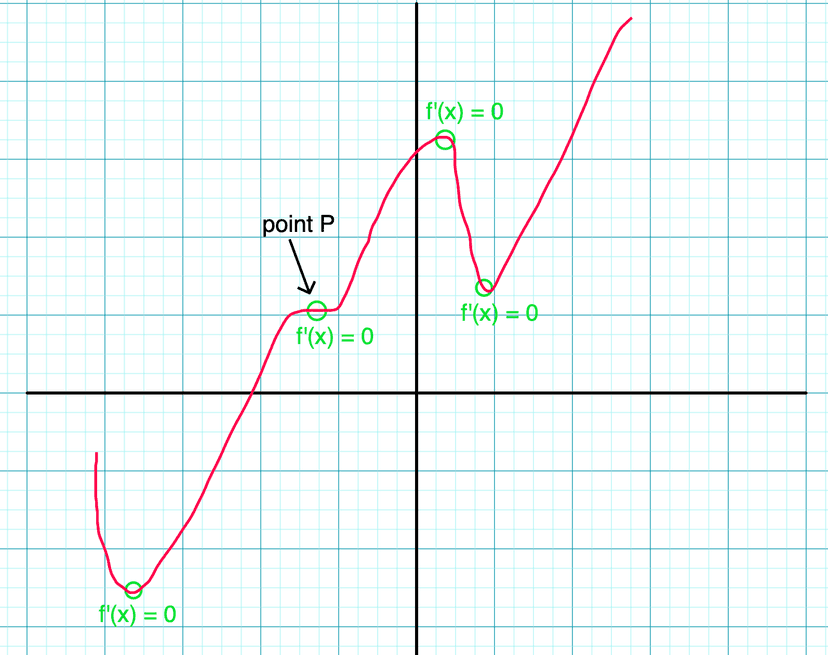
🔍 To identify critical points:
- is equal to
- is undefined
From there, you can check the critical points to determine if the value qualifies as extrema. We will cover that in a later topic, so stay tuned!
🧮 Practice Problems
1) Identifying Critical Points from a graph
Given the graph of , what points of the function would be critical points on the interval ?
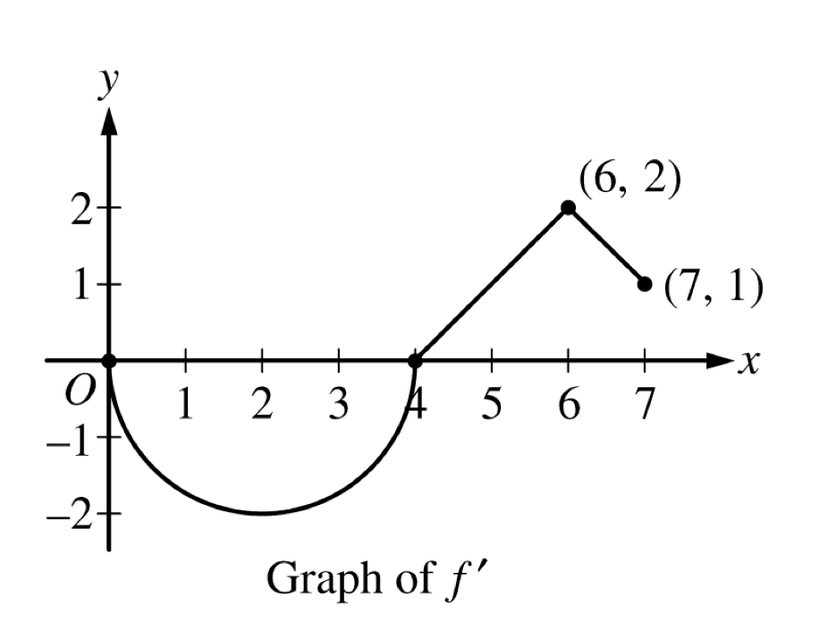
Let’s recall that at a critical point, the derivative either equals or does not exist. Therefore, we just have to check the graph of to see when it equals ! Since at and , we can conclude there are two critical points at and on the interval . You're on fire! 🔥
2) Identifying Extrema from a Graph
Given the graph of , identify if all critical points qualify as extrema, and identify an absolute maximum and minimum on the interval .
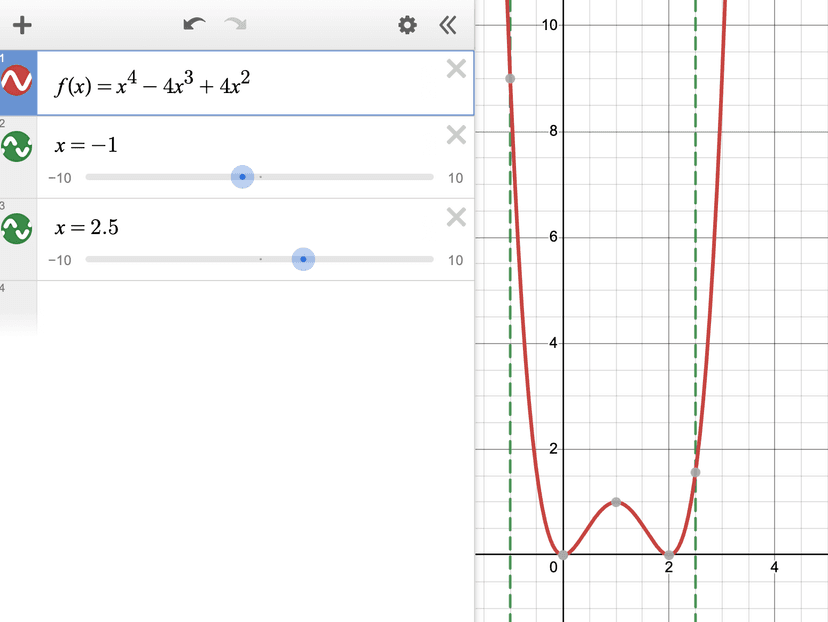
First, let's look at all of the critical points. At we have a local minimum since all surrounding points have a greater value. This is also the same for . Because these two points are also the lowest in the interval, and are absolute minimums.
Then, the other critical point is a local maximum since all of its surrounding values are lower.
Finally, we can take a look at the endpoints. The point must be the absolute maximum value of this function on the interval because it is higher than all of the other points in the interval. The point is only a local maximum, because it is higher than the points we can see in the interval. Nice job! 👍
3) Extreme Value Theorem
A function is defined as on the interval . Is the function guaranteed to have a maximum and minimum value in this interval?
Consider the requirements to apply the Extreme Value Theorem: the function must be continuous. However, the question does not supply the information that is continuous in the interval, or give us an equation to manually determine continuity. Therefore, we must conclude that the function is not guaranteed a maximum and minimum value on the interval .
🌟 Closing
Amazing work! 🙌 Understanding extreme values, global versus local extrema, and critical points is fundamental for tackling AP Calculus questions. You can anticipate encountering questions involving extrema and the Extreme Value Theorem on the exam, both in multiple-choice and as part of a free response.
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| continuous | A function that has no breaks, jumps, or holes in its graph over a given interval. |
| critical point | A point in the domain of a function where the derivative is zero or undefined, which are candidates for local and absolute extrema. |
| Extreme Value Theorem | A theorem stating that if a function is continuous on a closed interval [a, b], then the function must attain both a minimum and maximum value on that interval. |
| first derivative | The derivative of a function, denoted f', which describes the rate of change and indicates where a function is increasing or decreasing. |
| maximum value | The largest output value that a function attains on a given interval. |
| minimum value | The smallest output value that a function attains on a given interval. |
| relative extrema | Maximum or minimum values of a function at a point relative to nearby points. |
Frequently Asked Questions
How do I find critical points of a function step by step?
Step-by-step to find critical points (CED FUN-1.C.2): 1. Know the domain: decide the interval you care about (open or closed). If it’s a closed interval [a,b], endpoints are candidates for absolute extrema (Extreme Value Theorem applies). 2. Compute f ′(x) wherever f is differentiable. 3. Solve f ′(x) = 0. Any x that satisfies this is a stationary critical point. 4. Find points where f is defined but f ′(x) does NOT exist (corners, cusps, vertical tangents)—these are critical points too (points of nondifferentiability). 5. Collect all candidates: stationary points, nondifferentiable points, and endpoints (if interval is closed). 6. Classify: use the First Derivative Test or Second Derivative Test to label local max/min (remember: all local extrema occur at critical points, but not every critical point is an extremum). For absolute extrema on [a,b], use the Candidates Test: evaluate f at all candidates and pick largest/smallest. This matches AP expectations in Topic 5.2. For refresher examples and practice, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and try problems at (https://library.fiveable.me/practice/ap-calculus).
What's the difference between local and global extrema?
A global (absolute) extremum is the highest or lowest function value over an entire domain or a given closed interval [a,b]. By the Extreme Value Theorem, a continuous f on [a,b] must have at least one absolute max and one absolute min on that interval. A local (relative) extremum is a peak or valley compared with nearby points—f(x0) is a local max/min if f(x0) ≥/≤ f(x) for x near x0. Key links to the CED: all local extrema occur at critical points (f′ = 0 or f′ doesn’t exist), but not every critical point is an extremum. Also remember endpoints can be absolute extrema even if they’re not critical points. On the AP exam you’ll often use the first-derivative test or the candidates test (check critical points and endpoints) to identify local vs. global extrema. For a quick refresher, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and practice problems (https://library.fiveable.me/practice/ap-calculus).
When does the Extreme Value Theorem actually apply?
The Extreme Value Theorem (EVT) applies exactly when a function f is continuous on a closed, bounded interval [a,b]. In that case (FUN-1.C.1) EVT guarantees at least one absolute maximum and one absolute minimum on [a,b]. Remember: endpoints count as possible absolute extrema, and interior extrema occur at critical points (where f′ = 0 or f′ doesn’t exist—FUN-1.C.2). If the interval is open or f is discontinuous on [a,b], EVT does not apply—you can’t guarantee global extrema. So on the AP exam, always check two things before invoking EVT: continuity on the whole closed interval and that the domain is [a,b]. For practice and quick review see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and the Unit 5 overview (https://library.fiveable.me/ap-calculus/unit-5).
How do I know if a critical point is a maximum or minimum?
If f′(c)=0 or f′ doesn't exist, c is a critical point—but that alone doesn’t tell you max or min (FUN-1.C.2–3). Use these steps: - On a closed interval [a,b] remember the Extreme Value Theorem guarantees at least one absolute min and max (check endpoints, too). - First Derivative Test: look at sign of f′ just left/right of c. If f′ goes + → −, c is a local (relative) max; if − → +, local min; if sign doesn’t change, not an extremum. (This is what AP often expects for justification.) - Second Derivative Test (when f″ exists): if f′(c)=0 and f″(c)>0 then local min; if f″(c)<0 then local max; if f″(c)=0 test is inconclusive. - For absolute extrema use the Candidates Test: evaluate f at critical points and endpoints, pick largest/smallest. Want practice? See the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and Unit 5 review (https://library.fiveable.me/ap-calculus/unit-5). For more problems, try the practice bank (https://library.fiveable.me/practice/ap-calculus).
What's the formula for finding where the derivative equals zero?
You don’t need a fancy formula—you just set the derivative equal to zero and solve. Steps: - Compute f′(x) using derivative rules. - Solve f′(x) = 0 for x (algebraically or numerically). Those solutions are stationary points (possible local extrema). - Also include x where f′(x) does not exist and endpoints of a closed interval—together these are the critical points used by the Candidates Test and Extreme Value Theorem (CED FUN-1.C.2, FUN-1.C.3). Quick examples: - If f(x) = x^n, f′(x) = n x^{n-1}, so set n x^{n-1} = 0 ⇒ x = 0. - If f(x) = ax^2 + bx + c, f′(x) = 2ax + b ⇒ 2ax + b = 0 ⇒ x = −b/(2a). Remember: finding f′(x) = 0 gives candidates for local/absolute extrema but you must test them (first-derivative test, second-derivative test, or compare values on the interval). For more on Topic 5.2 see the study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and practice problems (https://library.fiveable.me/practice/ap-calculus).
I don't understand why some critical points aren't extrema - can someone explain?
A critical point is any x where f′(x)=0 or f′ doesn’t exist, but that alone doesn't force a max or min. Think of three reasons why a critical point might not be an extremum: - Inflection (change in concavity): f′(c)=0 but f changes concavity there, so f goes from increasing to increasing (or decreasing to decreasing). Example: f(x)=x^3 at x=0—f′(0)=0 but no local max/min. - Horizontal tangent on a plateau of monotonicity: derivative zero but sign of f′ doesn’t change (positive→0→positive), so the function keeps increasing overall. - Nondifferentiable critical point that’s not extreme: cusp or corner can be extremum (like |x| at 0) or not, depending on the surrounding behavior. To decide if a critical point is a local extremum use the First Derivative Test (check sign changes of f′) or the Second Derivative Test (if f′(c)=0 and f″(c)>0 → local min, f″(c)<0 → local max; if f″(c)=0 inconclusive). Remember all local extrema occur at critical points, but not all critical points are extrema (FUN-1.C.3). For more examples and AP-style practice, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and try problems at Fiveable’s practice page (https://library.fiveable.me/practice/ap-calculus).
When do I use the Extreme Value Theorem vs just finding derivatives?
Use the Extreme Value Theorem (EVT) when you need to guarantee existence of absolute (global) max/min on a closed interval [a,b]: if f is continuous on [a,b], EVT tells you there is at least one absolute max and min (FUN-1.C.1). EVT doesn’t find the points—it only assures they exist. So combine tools: on a closed interval, use the Candidates/Test method—check critical points (where f′ = 0 or f′ fails to exist, FUN-1.C.2) AND the endpoints, then compare f-values to find absolute extrema (this matches AP’s Candidates Test/Unit 5 tasks). Use derivatives (first-derivative test or second derivative) when you’re locating or classifying local (relative) extrema—all local extrema occur at critical points (FUN-1.C.3), but not every critical point is an extremum. Quick rule: EVT = existence on continuous [a,b]; derivatives = locate/classify extrema (and don’t forget endpoints for absolute extrema). For more AP-aligned practice and explanation, see the topic study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and tons of practice problems (https://library.fiveable.me/practice/ap-calculus).
How do I solve for critical points when the derivative doesn't exist?
If f′ doesn’t exist at some x, that x can still be a critical point—and those are exactly the places you must check for local/absolute extrema. Quick checklist you can use on the AP: 1. Find all x where f′(x) = 0 (stationary points). 2. Find all x in the domain where f′(x) fails to exist (point of nondifferentiability): corners, cusps, vertical tangents, or where algebra gives division by zero. Include only x inside the interval you care about. (FUN-1.C.2) 3. If you’re on a closed interval [a,b], include endpoints a and b (EVT requires continuity on [a,b] to guarantee global extrema). (FUN-1.C.1) 4. Use the First Derivative Test or compare function values (Candidates Test) to decide whether those critical points are local or absolute extrema. (FUN-1.C.3) So: compute f′, solve f′=0, list where f′ DNE (check that f is defined/continuous there), and evaluate f at all candidates and endpoints. For a step-by-step guided read, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo). For extra practice, try problems at the unit page (https://library.fiveable.me/ap-calculus/unit-5) or the large practice set (https://library.fiveable.me/practice/ap-calculus).
What's the difference between absolute and relative extrema?
Absolute (global) extrema are the highest or lowest function values over an entire domain (or a closed interval [a,b]). If f is continuous on [a,b], the Extreme Value Theorem guarantees at least one absolute max and one absolute min on [a,b] (CED FUN-1.C.1). Relative (local) extrema are highs or lows compared to nearby points: f has a local max/min at c if f(c) ≥ f(x) (or ≤) for x in some small neighborhood around c. By Fermat’s theorem, local extrema (except endpoints) occur at critical points where f′(c)=0 or f′ fails to exist (CED FUN-1.C.2–3), but not every critical point is a local extremum. Endpoints can be absolute extrema, so use the candidates/test: check critical points and endpoints to find absolute extrema on a closed interval (Topic 5.5). For deciding local behavior, use the first-derivative test (Topic 5.4). More review: see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo), Unit 5 overview (https://library.fiveable.me/ap-calculus/unit-5), and extra practice (https://library.fiveable.me/practice/ap-calculus).
Can a function have extrema that aren't at critical points?
Short answer: yes—but only in certain places. Why: By the CED, a critical point is where f′(x)=0 or f′ fails to exist. Fermat’s theorem applies to interior local extrema: any local (interior) max or min must occur at a critical point. However, on a closed interval [a,b] the Extreme Value Theorem guarantees absolute extrema may occur at the endpoints a or b. Endpoints need not be critical points. Example: f(x)=x on [0,1] has absolute min at 0 and max at 1, but f′(x)=1 everywhere (no critical points). What to do on the exam: when you find global extrema on a closed interval, use the Candidates Test—check all critical points AND the endpoints. For local extrema inside the domain, check where f′=0 or DNE and then use the First Derivative Test (see the Topic 5.2 study guide for a quick recap: (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo)). For more practice, try problems at (https://library.fiveable.me/practice/ap-calculus).
How do I find the absolute maximum and minimum on a closed interval?
First check the hypothesis: if f is continuous on the closed interval [a,b], the Extreme Value Theorem guarantees at least one absolute max and min. Then use the Candidates (or closed-interval) method: 1. Find critical points inside (a,b): solve f′(x)=0 and note where f′ fails to exist (FUN-1.C.2). 2. Make a list of candidates: all those interior critical points plus the two endpoints a and b (endpoints can be absolute extrema). 3. Evaluate f at each candidate. 4. The largest value is the absolute maximum on [a,b]; the smallest is the absolute minimum. On the AP exam you should justify continuity on [a,b] (FUN-1.C.1) and show the calculus work (solve f′=0 or argue nondifferentiability). For practice and worked examples see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo), the Unit 5 overview (https://library.fiveable.me/ap-calculus/unit-5), and more practice problems (https://library.fiveable.me/practice/ap-calculus).
I'm confused about continuous functions - does the Extreme Value Theorem work on open intervals?
Short answer: no—the Extreme Value Theorem (EVT) requires the function to be continuous on a closed interval [a, b]. If f is continuous on [a, b], EVT guarantees at least one absolute (global) minimum and maximum on that closed interval (CED FUN-1.C.1). On an open interval (a, b) the theorem doesn’t apply, so extrema might not exist. Why: endpoints matter. For example, f(x)=x on (0,1) is continuous but has no absolute max or min on (0,1) because values approach 0 and 1 only at the endpoints (not included). Or f(x)=1/x on (0,1) has no maximum—it blows up as x→0+. In AP language: to justify that an absolute extremum exists you must show continuity on a closed interval [a,b] (use EVT); otherwise check critical points and endpoint values (Candidates Test) when the interval is closed (topics 5.2–5.5). For a deeper read and practice on this topic, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo), the Unit 5 overview (https://library.fiveable.me/ap-calculus/unit-5), and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).
What are the steps to find all extrema of a function on [a,b]?
1. Check hypotheses: if f is continuous on [a,b], the Extreme Value Theorem (FUN-1.C.1) guarantees at least one absolute max and min. If continuity fails, endpoints or discontinuities need special care. 2. Find critical points: compute f′(x) and solve f′(x)=0; also list points where f′(x) does not exist (FUN-1.C.2). Keep only those in (a,b). 3. Build the candidate set: all critical points in (a,b) plus the two endpoints a and b (endpoint extrema can occur). 4. Evaluate f at every candidate. The largest value is the absolute (global) maximum; the smallest is the absolute minimum (Candidates/Test). 5. For local (relative) extrema: use the First Derivative Test (or sign chart) at each critical point—if f′ changes +→− you have a local max, −→+ a local min; no sign change → not an extremum (FUN-1.C.3). 6. State/justify your conclusion referencing EVT and Fermat’s theorem. Need practice? See the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo), the Unit 5 overview (https://library.fiveable.me/ap-calculus/unit-5), and tons of problems (https://library.fiveable.me/practice/ap-calculus).
Why do I have to check the endpoints when finding absolute extrema?
Because the Extreme Value Theorem only guarantees an absolute max and min on a closed, continuous interval [a,b], you have to check every possible candidate where those extrema could occur—and that includes the endpoints. Critical points (where f′ = 0 or f′ fails to exist) give you interior candidates, but Fermat’s theorem doesn’t say anything about endpoints. So the Candidates Test for absolute (global) extrema says: evaluate f at all critical points inside (a,b) and at a and b, then pick the largest and smallest values. An endpoint can be the absolute max or min even when f′(endpoint) ≠ 0 (or isn’t defined there), so skipping endpoints risks missing the true global extrema on [a,b]. This is exactly what the CED calls “endpoint extrema” and ties into FUN-1.C and FUN-1.C.2. For a quick refresher, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo). For more practice, try problems at the Unit 5 page (https://library.fiveable.me/ap-calculus/unit-5) or the practice set (https://library.fiveable.me/practice/ap-calculus).
How do I tell if a function is continuous enough to use the Extreme Value Theorem?
You can use the Extreme Value Theorem (EVT) only when its hypotheses are met: the function must be continuous on a closed interval [a,b]. “Continuous enough” means no breaks, jumps, or infinite values anywhere on that entire interval—including at the endpoints. If f is continuous at every x in [a,b], EVT (FUN-1.C.1) guarantees at least one absolute max and one absolute min on [a,b]. Quick checks: - Standard continuous families (polynomials, exponentials, sines/cosines) are continuous everywhere—so EVT applies on any closed [a,b]. - Rational functions are continuous where the denominator ≠ 0—ensure no zeros of the denominator lie in [a,b]. - Piecewise functions: verify continuity at the joining points and at endpoints. - If f is differentiable on (a,b) and continuous at the endpoints, you’re safe (differentiability ⇒ continuity). When searching for extrema, evaluate critical points (f′=0 or undefined) inside (a,b) and also check the endpoints. For more examples and practice, see the Topic 5.2 study guide (https://library.fiveable.me/ap-calculus/unit-5/extreme-value-theorem-global-vs-local-extrema-critical-points/study-guide/xcQI1ZzNbmWJ5uRNiFCo) and unit resources (https://library.fiveable.me/ap-calculus/unit-5).