2.2 Defining the Derivative of a Function and Using Derivative Notation

AI

Welcome back to AP Calculus with Fiveable! This topic focuses on determining derivative notation and calculating the derivative of a function. Let's combine our skills in calculating rates of change with the knowledge of limits to continue building our derivative skills. 🧱

↗️ Definition of Derivative

The derivative of a function at a single point is the instantaneous rate of change at that point. We learned how to calculate an instantaneous rate of change in the previous topic: Defining Average and Instantaneous Rates of Change at a Point.

But how can we find the derivative of the whole curve, instead of at just one single point? It would be far too tedious to calculate the instantaneous rate of change at every single point, and then graph. 🤔

We can actually find the derivative by generalizing the limit notation and not solving for the derivative at the point. Therefore, we use the limit definition of a derivative:

$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$

You will learn certain rules and shortcuts to calculating derivatives in the next few lessons, but for now, we will use the definition of the derivative to calculate the rate of change for a function.

Graph of a tangent line, created with Desmos

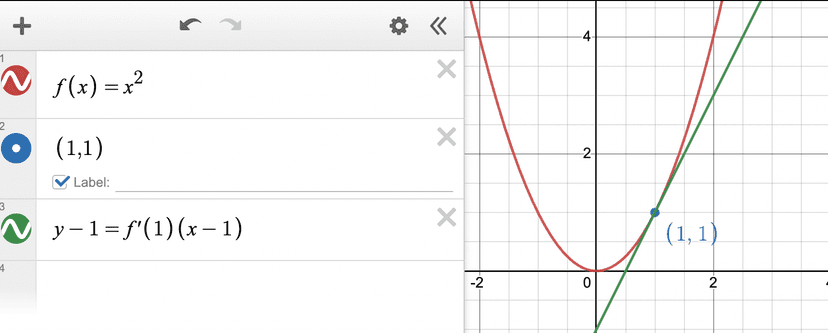
We can see that the slope of the tangent line is $f'(1)$, or the derivative of $f(x)$ when $x = 1$.

📝 Derivative Notation

There are several ways to represent a derivative in calculus.

If the original function can be represented as $y = f(x)$, then the derivative can be represented as $y'$, $f'(x)$, or $\frac {dy}{dx}$. These all describe the rate of change of the function as the dependent variable changes.

To reiterate,

$y' = f'(x) = \frac{dy}{dx}$

They are all valid, and mean the same thing!

---

🧮 Practice Problems

Let’s work on a few questions and make sure we have the concept down!

1. Using the Definition of a Derivative

Given $y = 3x^2 + 4x$, calculate $y'$.

Let’s plug in all of the given information to the limit. Since $y = f(x)$,

$y' = \lim_{h \to 0} \frac{[3(x + h)^2 + 4(x+h)]- [3x^2+4x]}{h}$

Let's simplify this so that we can take the limit and determine how the function changes. We can begin by expanding the numerator and then distributing it.

$y'= \lim_{{h \to 0}} \frac{{3(x^2 + 2xh + h^2) + 4(x+h)-(3x^2 + 4x)}}{h}$

$y'= \lim_{{h \to 0}} \frac{{3x^2 + 6xh + 3h^2 + 4x + 4h - 3x^2 -4x}}{h}$

Now, let’s combine like terms.

$y'= \lim_{{h \to 0}} \frac{{6xh + 3h^2 + 4h}}{h}$

We are almost there! Since $h \neq 0$, we can divide by $0$.

$y' = \lim_{{h \to 0}} (6x + 3h + 4)$

As $h$ approaches $0$, the middle term will approach $0$. Therefore, we conclude:

$y' = 6x + 4$

Amazing work! 🎉

2) Tangent Line to a Curve

Given the curve $f(x) = \frac {1}{x}$, find the equation of the line tangent to the curve at $(1,1)$.

Let’s use the definition of derivative to first calculate the derivative at $(1,1)$.

$f'(x) = \lim_{{h \to 0}} \frac{\frac{1}{{x + h}} - \frac{1}{x}}{h}$

This might seem a bit intimidating, but here we can change the two fractions in the numerator to have a common denominator.

In the numerator, we then have $\frac{x - (x + h)}{x(x + h)}$. Therefore…

$f'(x) = \lim_{{h \to 0}} \frac{\frac{x - (x + h)}{x(x + h)}}{h}$

Now, we can multiply the numerator by the reciprocal of the denominator.

$f'(x) = \lim_{{h \to 0}} {\frac{x - (x + h)}{x(x + h)}}*{\frac{1}{h}} = f'(x) = \lim_{{h \to 0}} {\frac{x - (x + h)}{x(x + h)(h)}}$

Now let’s expand the numerator.

$f'(x) = \lim_{{h \to 0}} {\frac{x - x - h}{x(x + h)(h)}}= \lim_{{h \to 0}} {\frac{- h}{x(x + h)(h)}}$

We can cancel the $h$ from both the numerator and the denominator to get

$f'(x) = \lim_{{h \to 0}} \frac{-1}{x (x + h)} = \lim_{{h \to 0}} \frac{-1}{x^2 + xh }$

As $h$ approaches $0$, the second term in the denominator will approach $0$, so we can conclude

$f'(x)= \frac{-1}{x^2}$

Now we need to write the equation of a tangent line! Remember that a line can be represented in point-slope form as the following: $y-y₁=m(x-x₁)$ where $m$ is the slope, or the derivative at the point $(x_1,y_1)$.

Our point is $(1,1)$, so $f'(1)= \frac{-1}{(1)^2} = -1$.

Now we have all of the necessary information to write the equation of the tangent line:

$y-1=-1(x-1)$

Great work! Let's check that this line is tangent to the curve $f(x)= \frac{1}{x}$ at the point $(1,1)$.

Graph of tangent line, created with Desmos

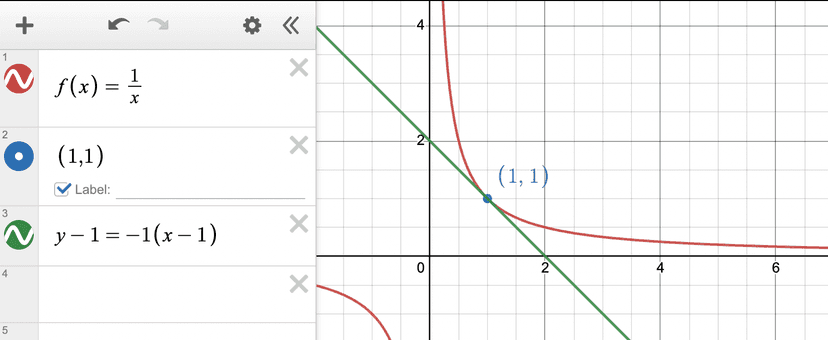
Looks great! 🙌

---

🌟 Closing

Great job! 🚀👩‍🚀 You're mastering these concepts, and with practice, you'll navigate derivatives and continuity with confidence. Determining derivatives and using different derivative notations are crucial skills in AP Calculus. As you encounter questions on the exam, remember to check for domain restrictions and assess piecewise continuity.