8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
Welcome to the third topic in Unit 8! In this key topic, we’ll be learning more about what an accumulation problem is and how to solve one. For a more in-depth review of how to take an integral, take a look at Unit 6!

⛰️ Accumulation Problems
So before we learn how to solve an accumulation problem, we need to know what an accumulation problem is in the first place. The picture below is a visual representation of the graphical meaning of an integral.
To calculate the integral of a function, you are essentially taking the area that is under the curve! More specifically in an accumulation problem, you are taking the integral of the rate of change function that you are given.
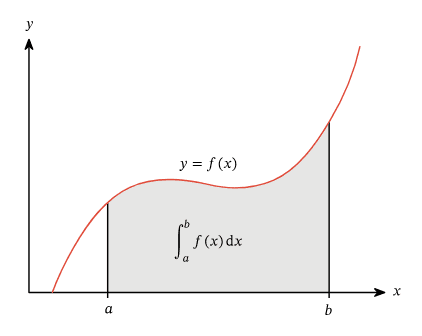
📝 Walkthrough of an Accumulation Problem
This will be a very simple example to understand the concept of accumulation. You are given a velocity equation, which is . How would you calculate the total displacement between and ?
Here’s one way we can solve the problem, step by step.
1️⃣ Identify the rate of change function.
In this case, the rate of change function is velocity since we want to end up with time!
2️⃣ Set up the definite integral to evaluate.
Why exactly is this the definite integral? Good question! 😄
The definition of velocity is the rate of change of the position. Since we are trying to find the displacement, it makes sense that we are taking the integral of the velocity.
💡 Also note that the derivative of position is velocity, so that means the integral of velocity is displacement (or net change in position)!
3️⃣ Evaluate the integral!
We get that the final displacement is !
📝 2004 AP Calculus AB Form B Question 2c Walkthrough
The following free-response question (FRQ) is from the 2004 AP Calculus AB examination from Form B administered by College Board. All credit to College Board.

For this problem, we are only working on Part C because that is the part that has to do with accumulation.
🪜Accumulation Function: Steps to Follow
1️⃣ Identify the rate of change function.
2️⃣ Set up the definite integral to find the net change.
3️⃣ Evaluate the integral.
4️⃣ Use any provided initial condition to complete the problem!
🔎 Step 1: Identifying the rate of change function
The function is given in the problem. Here it is below! Remember that the units for the rate of change is mosquitoes per day 🦟.
📕 Steps 2 & 3: Setting up and evaluating the definite integral
In Part C, we’re trying to find the number of mosquitoes on the island at , which means we are trying to find the accumulation of the rate of change from to .
✅ Step 4: Using the initial condition
In the problem you are told that at , there are 1000 mosquitoes on the island. Since we calculated the total change, we can add that to our initial condition to get the final answer!
Since the final answer says to round to the nearest whole number, the final answer will be 964 mosquitoes! 🦟
⭐️ Closing
Congrats on making it through the application part of the accumulation problems. With continuous practice, you’ll learn more and be able to ace the AP Calculus exam! You’ve got this! ☺️
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| accumulation | The process of gathering or building up a quantity over time or over an interval, which can be expressed and calculated using definite integrals. |
| definite integral | The integral of a function over a specific interval [a, b], representing the net signed area between the curve and the x-axis. |
| net change | The total change in a quantity over an interval, calculated as the difference between final and initial values, often found using definite integrals. |
| rate of change | The measure of how quickly a quantity changes with respect to another variable, often time. |
Frequently Asked Questions
How do I know when a problem is asking for accumulation vs just a regular integral?
Look for whether the integrand is a rate (units like meters/sec, people/hour, ft^3/min) or the problem asks “how much” or “net change” over an interval. If the integrand is a rate of change, the definite integral gives accumulation (net change theorem, CHA-4.D/CHA-4.E): ∫a^b rate(t) dt = net change of the quantity on [a,b]. If the problem asks for area with no context or just asks to evaluate an antiderivative, treat it as a “regular” integral computation. Watch for signed area vs total amount: velocity integrates to displacement (signed); to get total distance you integrate |v(t)|. Also check for initial conditions—accumulation functions often appear as F(x)=∫a^x r(t) dt plus F(a). Practice spotting rates and units on AP-style problems (this is tested in Unit 8). For extra examples, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and try practice problems (https://library.fiveable.me/practice/ap-calculus).
What's the difference between net change and total change when using definite integrals?
Net change = the definite integral of a rate of change over an interval. It’s the signed accumulation (use the Net Change Theorem): ∫_a^b r(t) dt gives how much the quantity has changed overall (can be positive, negative, or zero). That’s what the CED calls “net change” (CHA-4.D). Total change (often called total distance) takes absolute value of the instantaneous rate before integrating: ∫_a^b |v(t)| dt. That measures how much quantity actually accumulated regardless of direction (always nonnegative). So for motion, net change = displacement, total change = total distance traveled. Key points for AP: interpret integrals as signed area (net change) vs area of |rate| (total/total-distance). Use an antiderivative + initial condition to get actual accumulated amount (accumulation function). See Topic 8.3 study guide for examples (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG). For extra practice, try problems at (https://library.fiveable.me/practice/ap-calculus).
I'm confused about accumulation functions - how is the integral of a rate giving me the actual amount?
Think of the integrand as “how fast something is changing” and the integral as adding up all those tiny changes. Net Change Theorem (CED CHA-4.D/CHA-4.E): if r(t) is the rate of a quantity Q (units: Q per time), then ∫_a^b r(t) dt = Q(b) − Q(a). So the definite integral gives the net change in Q over [a,b]. Example: if water flows at r(t)=3 gallons/min for 5 minutes, ∫_0^5 3 dt = 15 gallons—that’s the actual amount added. More generally Q(b)=Q(a)+∫_a^b r(t) dt, so you need the initial amount Q(a) to get the total. Key ideas for AP: interpret the integrand as a rate, treat the integral as signed area (positive/negative rates give net change), and know displacement vs total distance (use |velocity| for distance). This is exactly what Topic 8.3 and CHA-4 in the CED test on the exam. For more review and examples see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and practice problems (https://library.fiveable.me/practice/ap-calculus).
When do I use definite integrals to find net change in word problems?
Use a definite integral to find net change whenever the thing you're integrating is a rate of change (units like m/s, people/hour, gallons/min). By the Net Change Theorem (CED CHA-4.D), ∫[a to b] rate(t) dt equals the net change of the quantity from a to b—that is signed area: increases minus decreases. Quick checklist: - Is the integrand a rate (velocity, flow rate, growth rate)? → use a definite integral for net change. - Do you need total distance (always positive)? → integrate speed |v(t)|, not v(t). - Do you want the accumulated amount from a known start? → use ∫ rate + initial condition to get the absolute value at time b. On the AP exam this shows up in applied contexts (Unit 8, CHA-4.E). For a focused review see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and practice problems (https://library.fiveable.me/practice/ap-calculus).
How do I solve problems where they give me a rate function and ask for the total accumulated amount?
Think of the rate function r(t) as "how fast" a quantity changes. The net accumulated amount from t = a to t = b is just the definite integral of that rate: - Net change = ∫[a to b] r(t) dt. By the Fundamental Theorem of Calculus, compute an antiderivative R(t) and evaluate R(b) − R(a). If you’re given an initial amount A(a), add it: A(b) = A(a) + ∫[a to b] r(t) dt. Key cautions from the CED (CHA-4.D / CHA-4.E): - The integral gives signed (net) change. If r(t) goes negative, that subtracts from the total. - If you need total amount traveled or total volume without cancellation (e.g., total distance), integrate |rate| or split the interval where r(t) changes sign and sum the positive areas. If no antiderivative is easy, approximate with Riemann sums (midpoint/trapezoid)—these appear on the AP exam. For more practice and examples see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and plenty of practice problems (https://library.fiveable.me/practice/ap-calculus).
What's the formula for finding net change using definite integrals?
Net change = the definite integral of a rate over an interval. If f'(t) is the rate of change of a quantity, then the net change from a to b is net change = ∫[a to b] f'(t) dt = F(b) − F(a), where F is any antiderivative of f'. More generally, if r(t) is a rate (flow, velocity, population growth, etc.), net change = ∫[a to b] r(t) dt. This follows from the Fundamental Theorem of Calculus and is exactly the AP CED idea that a definite integral of a rate gives net change (CHA-4.D, CHA-4.E). Note: “net” uses signed area (positive and negative cancel). If you need total amount (e.g., total distance traveled), use ∫[a to b] |v(t)| dt instead. For more examples tied to AP expectations, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and the Unit 8 overview (https://library.fiveable.me/ap-calculus/unit-8). For practice, check Fiveable’s problem set collection (https://library.fiveable.me/practice/ap-calculus).
Can someone explain step by step how to set up an accumulation problem with integrals?
Think of an accumulation problem as “start amount + net change.” Step-by-step: 1. Identify the rate function r(t) (units: quantity/time). The integrand must be a rate (CED: “integrand as rate function”). 2. Pick the interval [a,b] over which you accumulate (time, distance, etc.). Include initial condition if given (initial amount). 3. Write the net change = ∫_a^b r(t) dt (CED CHA-4.D: definite integral of a rate gives net change). This gives signed net change; if you need total amount added regardless of sign (total distance vs displacement), integrate |r(t)|. 4. If initial amount A(a) is given, final amount = A(a) + ∫_a^b r(t) dt. If not, the integral itself is the net change. 5. Evaluate using an antiderivative (FTC) or approximate with Riemann/midpoint sums if data/tabled (AP free-response often asks for midpoint sums). For examples and practice aligned to Topic 8.3, see the Fiveable study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and more problems at (https://library.fiveable.me/practice/ap-calculus).
I don't understand why integrating velocity gives me displacement - shouldn't it give me something else?
Integrating velocity gives displacement because velocity is the rate of change of position. By the Net Change Theorem (CED CHA-4.D.2), the definite integral ∫[a to b] v(t) dt equals the net change in position = x(b) − x(a). That’s signed area under the v(t) curve: positive area moves you forward, negative area moves you backward. If you want the actual position you need an initial condition x(a); then x(b) = x(a) + ∫[a to b] v(t) dt. What you might’ve expected instead is total distance traveled—that’s different: total distance = ∫[a to b] |v(t)| dt (integral of speed), which removes sign. On the AP exam, be ready to interpret definite integrals as net change (displacement) and distinguish displacement vs total distance (CED keywords: net change theorem, signed area, integrand as rate function). For a quick review, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and try practice problems (https://library.fiveable.me/practice/ap-calculus).
How do I know what my limits of integration should be in accumulation problems?
Pick your limits from the real-world interval you care about—they’re just the start and end times/positions of the accumulation. The definite integral of a rate over [a,b] gives the net change from a to b (CED CHA-4.D, CHA-4.E). So: - If a problem asks “how much from t = 0 to t = 3?” use ∫₀³ r(t) dt. - If it asks “net change between yesterday (t = 2) and today (t = 8)?” use ∫₂⁸ rate(t) dt. - If you have an accumulation function A(x)=∫₃ˣ f(t) dt, the lower limit (3) is the starting amount/time and x is the variable end. Watch sign: integrals give signed (net) change. For total distance (particle motion) split at times where velocity = 0 and integrate |v(t)| on each subinterval, then add. If you need the new amount, add the initial condition: amount(b)=amount(a)+∫ₐᵇ rate(t) dt. For more AP-aligned examples and practice, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG), the Unit 8 overview (https://library.fiveable.me/ap-calculus/unit-8), and thousands of practice problems (https://library.fiveable.me/practice/ap-calculus).
When they say "net change over an interval" do I always use a definite integral?
Short answer: usually, yes—net change of a quantity that’s given by a rate is computed with a definite integral (the Net Change Theorem). If f(t) is a rate (like v(t) or flow rate), then the net change from a to b is ∫_a^b f(t) dt = F(b) − F(a), where F is an antiderivative (Fundamental Theorem of Calculus). Always include units (e.g., vehicles, meters). Important caveats you’ll see on the AP: - "Net change" means signed area: positive and negative contributions cancel (displacement = ∫ v dt). - If the question asks for total amount traveled (total distance), use ∫_a^b |v(t)| dt instead. - If the rate is given only at discrete times, approximate the definite integral with a Riemann sum (midpoint/left/right) as the exam often requires. - If the rate isn’t integrable/continuous, state conditions or use appropriate sums. For practice and review on Topic 8.3, see the Fiveable study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and try problems from the unit (https://library.fiveable.me/ap-calculus/unit-8) or the practice bank (https://library.fiveable.me/practice/ap-calculus).
What's the difference between finding total distance traveled vs displacement using integrals?
Displacement = net change: integrate the velocity v(t) on [a,b]. By the Net Change Theorem, ∫_a^b v(t) dt = x(b) − x(a). This is signed area under the v(t) curve (positive area minus negative area). That’s what the AP CED calls the “definite integral of a rate” and gives net change (CHA-4.D, CHA-4.E). Total distance traveled = accumulate speed: integrate the speed |v(t)|. So distance = ∫_a^b |v(t)| dt. Practically you find times where v(t)=0, split the interval at those zeros, and sum ∫ over subintervals with sign removed (i.e., take −∫ if v<0 so each piece is positive). On the AP exam, be ready to (1) use ∫ v to get displacement and (2) split at sign changes and use ∫ |v| (or sum of absolute-value integrals) for total distance. For a quick review, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG). Fiveable also has practice problems if you want more examples (https://library.fiveable.me/practice/ap-calculus).
How do I interpret what a definite integral means in real world context problems?
A definite integral in a real-world problem is an accumulation of a rate—think “rate × time”—and it gives the net change of the quantity over the interval (CED: CHA-4.D, CHA-4.E). Concretely: if r(t) is a rate (cars/hr, gallons/min, current in A), then ∫[a to b] r(t) dt = change in total cars/gallons/charge from t=a to t=b. Use units every time (cars/hr × hr = cars). Remember signed area: positive parts add, negative parts subtract (so the integral gives net change or displacement); to get total amount traveled or total poured (always positive) you integrate the absolute value of the rate. Use an antiderivative and the Fundamental Theorem of Calculus to evaluate integrals in closed form, or Riemann/midpoint sums to approximate from data (AP exam often asks both). For more examples and AP-style practice, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG), the Unit 8 overview (https://library.fiveable.me/ap-calculus/unit-8), and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).
I keep getting confused about whether to use positive or negative values in accumulation problems - help?
Short version: whether you keep negative values depends on what you’re accumulating. The definite integral of a rate gives net change (signed area)—positives add, negatives subtract (CHA-4.D, CHA-4.E). For example, ∫ v(t) dt = displacement (can be negative); but total distance = ∫ |v(t)| dt (take absolute value before integrating). Use the integrand’s sign: a negative flow rate means the quantity is decreasing, so include the negative when you want net change; take absolute values only when the problem explicitly asks for “total,” “amount,” or “distance traveled.” Always apply initial conditions: accumulation function A(x)=A(a)+∫_a^x rate(t) dt gives the current amount (signed net change). On the AP exam, the prompt will usually indicate whether it wants net change (use sign) or total/amount (use absolute value)—justify your choice. For more examples and practice, see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG), the Unit 8 overview (https://library.fiveable.me/ap-calculus/unit-8), and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).
How do I solve FRQ questions that ask about water flowing in and out of a tank using integrals?
Think of the integrand as a rate (volume/time). The net change theorem (CED CHA-4.D / CHA-4.E) says the definite integral of a rate gives the net change of the quantity. For a tank with inflow r_in(t) and outflow r_out(t): - Write net rate: r_net(t) = r_in(t) − r_out(t). - Net change from a to b: ΔV = ∫_a^b r_net(t) dt. - Current volume: V(b) = V(a) + ΔV. Include the initial condition V(a). Units should be volume (e.g., liters or gallons). If they give only discrete data, use a Riemann sum or midpoint/trapezoid approximation and state units. If rates can be negative, remember the integral gives signed area (so outflow larger than inflow yields negative ΔV). On FRQs, always: (1) write the integral expression, (2) evaluate or approximate it (FTC or numerical), and (3) interpret the result with units. For extra practice see the Topic 8.3 study guide (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and more problems at (https://library.fiveable.me/practice/ap-calculus).
What does it mean when they say "a function defined as an integral represents accumulation of a rate of change"?
Saying “a function defined as an integral represents accumulation of a rate of change” means: if r(t) is a rate (like velocity, flow rate, or population change), then A(x) = ∫a^x r(t) dt gives how much of the quantity has accumulated from time a to x. By the Net Change Theorem (CED CHA-4.D / CHA-4.E), that definite integral equals the net change of the original quantity (final − initial). Interpret the integrand as a rate and the integral as signed area under its curve: positive area adds to the total, negative area subtracts (displacement vs total distance depends on sign). The Fundamental Theorem of Calculus connects A′(x)=r(x) so A tracks accumulation and r is its instantaneous rate. For AP problems, practice setting up ∫ rate dt to get net change and remember to include units (e.g., ounces, vehicles). See the Topic 8.3 study guide for worked examples (https://library.fiveable.me/ap-calculus/unit-8/using-accumulation-functions-definite-integrals-applied-contexts/study-guide/nUlJKvXqRcsfLnVMd5fG) and more practice at (https://library.fiveable.me/practice/ap-calculus).