upgrade
Fiveable

♾️AP Calculus AB/BC Unit 6 Review

QR code for AP Calculus AB/BC practice questions

6.3 Riemann Sums, Summation Notation, and Definite Integral Notation

♾️AP Calculus AB/BC
Unit 6 Review

6.3 Riemann Sums, Summation Notation, and Definite Integral Notation

Written by the Fiveable Content Team • Last updated September 2025
Verified for the 2026 exam
Verified for the 2026 exam•Written by the Fiveable Content Team • Last updated September 2025
♾️AP Calculus AB/BC
Unit & Topic Study Guides
Unit 6 Overview: Integration and Accumulation of Change
6.1 Integration and Accumulation of Change
6.2 Approximating Areas with Riemann Sums
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
6.4 The Fundamental Theorem of Calculus and Accumulation Functions
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
6.6 Applying Properties of Definite Integrals
6.7 The Fundamental Theorem of Calculus and Definite Integrals
6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
6.9 Integrating Using Substitution
6.10 Integrating Functions Using Long Division and Completing the Square
6.11 Integrating Using Integration by Parts
6.12 Integrating Using Linear Partial Fractions
6.13 Evaluating Improper Integrals
6.14 Selecting Techniques for Antidifferentiation (AB)
Pep mascot

6.3 Riemann Sums, Summation Notation, and Definite Integral Notation

So far in Unit 6, we’ve learned how to approximate the area under the curve. But what if we wanted to find its exact value? For that, we’ll need to learn about integrals and how they are related to the Riemann sum. We’re bringing limits back! 🧠

Pep mascot
more resources to help you study
practice questionscheatsheetscore calculator

Σ Summation Notation

Before we get into integrals, we first need to learn how to make taking a Riemann sum faster. To do this, we’ll introduce summation notation so that we can apply algebra instead of manually computing the Riemann sum.

Let’s consider the function f(x)=x2f(x)=x^2 over the interval 0 to 5:

Untitled
Desmos graph of f(x)=x2f(x) = x^2 with area under the curve from [0,5][0,5] shaded.

Now, let’s use a left Riemann sum with 5 subintervals to approximate this area.

Untitled
The same Desmos graph with 5 left-endpoint Riemann rectangles.

To convert this to summation notation, we need to create a function that will give us the area of each rectangle. For now, let’s name this function AA so that A(i)A(i) gives us the area of the iith rectangle. With this function, we can write the Riemann sum as:

∑i=04A(i)\sum_{i=0}^{4}A(i)

Now that we have our summation notation, we need to find an expression for A(i)A(i). We know that the area of the rectangle will be b⋅hb\cdot h, where bb is the width of the base and hh is the height.

The width of our base will be constant, and we can find it by dividing the entire interval by the number of subintervals we want:

5−05=1\frac{5-0}{5}=1

The height is a little more tricky to notate, but it is just the value of the function ff at each of the left endpoints. To find this next (or iith) point, let’s first find the x-value, which we’ll denote as xix_i. To do this, we start at 0 and repeatedly add 1, the length of our subinterval.

PNG image 23.png
A graph demonstrating the relationship between the length of the subinterval and xix_i.

We can write the formula for this x-value as 1i1i or just ii. We can obtain the y-value, or height, by simply plugging in this formula for the x-value to our original formula like so: yi=(i)2y_i=(i)^2.

We can put these two things together in the area formula as:

A(i)=1⋅i2A(i)=1\cdot i^2

which simplifies to

A(i)=i2A(i)=i^2

Now, we simply plug that back into our summation notation:

∑i=15i2\sum_{i=1}^{5}i^2

✏️ General Form of Riemann Sum

The general form for the Riemann sum in summation notation is as follows:

∑i=0n−1Δx⋅f(xi)\sum_{i=0}^{n-1} {\Delta x}\cdot{f({x_i})}

for left-endpoint, and

∑i=1nΔx⋅f(xi)\sum_{i=1}^{n} {\Delta x}\cdot{f({x_i})}

for right-endpoint.

Let’s break down what each symbol means!

  • nn: This denotes the number of subintervals, and is usually given in the problem
  • aa: The lower bound of the interval.
  • bb: The upper bound of the interval.
  • Δx\Delta x: This is the width of each subinterval, and can be calculated by using the formula b−an\frac{b-a}{n}.
  • xix_i: This denotes the right endpoint for each rectangle, such that xi=a+Δx⋅ix_i=a+\Delta x\cdot i.
  • f(xi)f(x_i): The original function with xix_i plugged in.
  • ∑\sum: Tells us to add up the values from 0→n−10\rightarrow n-1 for left Riemann sums or 1→n1\rightarrow n for right Riemann sums.

Whew! That’s a lot of pieces to put together. 🧩

∫ Connecting to Definite Integrals

We learned in the last lesson that our Riemann sum becomes more precise if we use more rectangles or a greater value for nn. But what if we could have infinite rectangles, with infinitely tiny widths?

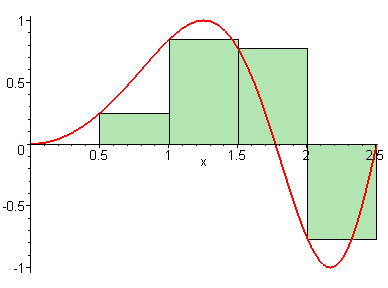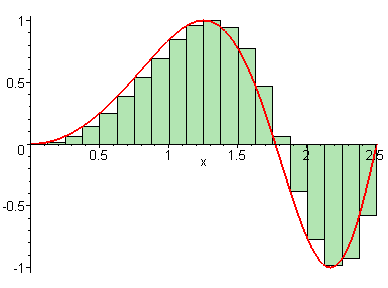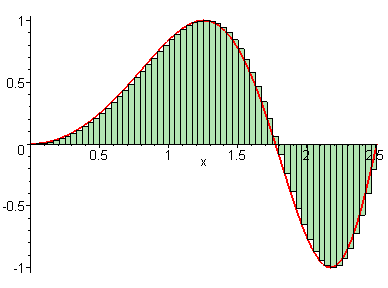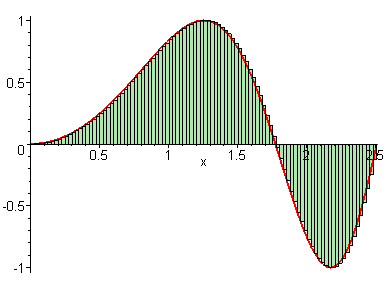
view.gif
GIF illustrating the left Riemann sum as n grows. GIF courtesy of Maplesoft

We see that as n→∞n\rightarrow \infty, our approximation for the area under the curve gets closer and closer to perfect. This means that we can connect the Riemann sum to the definite integral like so:

lim⁡n→∞∑i=1nΔx⋅f(xi)=∫abf(x) dx\lim_{n\to \infty}\sum_{i=1}^{n} {\Delta x}\cdot{f({x_i})}=\int_a^bf(x)\ dx

Where Δx=b−an\Delta x=\frac{b-a}{n} and xi=a+Δx⋅ix_i=a+\Delta x\cdot i.

The truly amazing thing is that this limit tells us the exact value for the definite integral—not just an approximation! 👌

📌 Connecting to Definite Integrals Walkthrough

Let’s connect all the dots and practice converting from summation to definite integral notation with this example problem!

Given the function f(x)=x2+3f(x)=x^2+3 over the interval [0,5][0,5], give the summation notation for the right Riemann sum using 10 subintervals and calculate its value. Then, write the definite integral as the limit of the right Riemann sum as nn approaches infinity.

1) Solving Summation Notation

The first part of the problem asks us to give and solve the summation notation with a fixed, finite nn. Let’s first write the general form without our area function defined:

∑i=110Δx⋅f(xi)\sum_{i=1}^{10}\Delta x\cdot f(x_i)

Now, we need to define our terms, starting with Δx\Delta x, which is defined as b−an=5−010=0.5\frac{b-a}{n}=\frac{5-0}{10}=0.5. Then, we need to define xix_i so that we can plug it into the original equation. To get the iith right endpoint, we use the formula a+Δx⋅ia+\Delta x\cdot i. In our case, a=0a= 0 and Δx=0.5\Delta x=0.5, so xi=0.5ix_i=0.5i. Now, we plug that back into our original equation to find that f(xi)=0.5i2+3f(x_i)=0.5i^2+3. Putting it all together, we find that the right Riemann sum using 10 subintervals is:

∑i=1100.5⋅(0.5i2+3)\sum_{i=1}^{10}0.5\cdot (0.5i^2+3)

The next part of the problem asks us to calculate this sum. This sum essentially tells us to plug in values from 1 to 10 and sum them all up, like so:

0.5(0.5(12)+3)+0.5(0.5(22)+3)+0.5(0.5(32)+3)+0.5(0.5(42)+3)+0.5(0.5(52)+3)+0.5(0.5(62)+3)+0.5(0.5(72)+3)+0.5(0.5(82)+3)+0.5(0.5(92)+3)+0.5(0.5(102)+3)0.5(0.5(1^2)+3)+0.5(0.5(2^2)+3)+0.5(0.5(3^2)+3)+0.5(0.5(4^2)+3)+0.5(0.5(5^2)+3)+0.5(0.5(6^2)+3)+0.5(0.5(7^2)+3)+0.5(0.5(8^2)+3)+0.5(0.5(9^2)+3)+0.5(0.5(10^2)+3)

This can be rewritten as

0.5(3.5+5+7.5+11+15.5+21+27.5+35+43.5+53)=111.250.5(3.5+5+7.5+11+15.5+21+27.5+35+43.5+53)=\boxed{111.25}

Lots of math, but not too bad, right?

2) Writing the Definite Integral

The final part of the problem asks us to write the definite integral as the limit of the right Riemann sum as nn approaches infinity. First, let’s write the definite integral:

∫05x2+3 dx\int_0^5x^2+3\ dx

Now, let’s remind ourselves of the general form for equation definite integrals to Riemann sums:

lim⁡n→∞∑i=1nΔx⋅f(xi)=∫abf(x) dx\lim_{n\to \infty}\sum_{i=1}^{n} {\Delta x}\cdot{f({x_i})}=\int_a^bf(x)\ dx

This is where things get a little tricky—since nn is the variable of our limit, we need to define our other terms in terms of nn.

  1. Let’s start by first defining Δx\Delta x as 5−0n=5n\frac{5-0}{n}=\frac{5}{n}.
  2. Then, let’s define xix_i in terms of nn, too. xi=a+Δx⋅i=0+5n⋅i=5nix_i=a+\Delta x\cdot i=0+\frac{5}{n}\cdot i=\frac{5}{n}i.
  3. Now let’s plug that back into f(x)f(x) to find that f(xi)=(5ni)2+3f(x_i)=(\frac{5}{n}i)^2+3.

Finally, let’s put that all back into our equation to get:

∫05x2+3 dx=lim⁡n→∞∑i=1n5n⋅[(5ni2)+3]\int_0^5x^2+3\ dx=\lim_{n\to \infty}\sum_{i=1}^{n} \frac{5}{n}\cdot \Bigg[ \Big( \frac{5}{n} i^2\Big)+3\Bigg]

These problems take a lot of practice, but once you commit the process for finding Δx\Delta x and xix_i to memory, they become very doable. Good luck! 🍀

✏️ Riemann Sum Practice

Try to tackle these three problems yourself! When you’re done, you can check out the solutions and how to walk through them.

❓Practice Problems

  1. For the function f(x)=4x2+2x−1f(x)=4x^2+2x-1, determine the definite integral ∫13f(x) dx\int_1^3f(x)\ dx as the limit of a Riemann sum.
  2. Express the definite integral ∫022ex+1 dx\int_0^2 2e^x+1 \ dx dx as the limit of a Riemann sum.
  3. The velocity function v(t)v(t) is given by v(t)=2t+1v(t)=2t+1 for the time interval [1,4][1,4]. Express the definite integral ∫14v(t) dt\int_1^4v(t)\ dt as the limit of a Riemann sum.

Answers below! ⬇️

📝 Solutions

Practice Problem 1 Solution

Start by defining Δx\Delta x in terms of nn: 3−1n=2n\frac{3-1}{n}=\frac{2}{n}. Then, do the same for xix_i: xi=a+Δx⋅i=1+2nix_i=a+\Delta x\cdot i=1+\frac{2}{n}i. Then, plug this in to f(x)f(x) to get:

f(xi)=4(1+2ni)2+2(1+2ni)−1f(x_i)=4(1+\frac{2}{n}i)^2+2(1+\frac{2}{n}i)-1

Finally, plug this all into the general limit equation to find that:

∫13f(x) dx=lim⁡n→∞∑i=1n2n⋅(4(1+2ni)2+2(1+2ni)−1)\int_1^3f(x)\ dx=\lim_{n\to \infty}\sum_{i=1}^n \frac{2}{n}\cdot \Bigg(4(1+\frac{2}{n}i)^2+2(1+\frac{2}{n}i)-1\Bigg)

The next question follows a very similar process.

Practice Problem 2 Solution

You can again start by defining Δx\Delta x in terms of nn: 2−0n=2n\frac{2-0}{n}=\frac{2}{n}. Then, do the same for xix_i: xi=a+Δx⋅i=0+2ni=2nix_i=a+\Delta x\cdot i=0+\frac{2}{n}i=\frac{2}{n}i. Then, plug this in to f(x)f(x) to get:

f(xi)=2e2i/n+1f(x_i)=2e^{2i/n}+1

Finally, plug this all into the general limit equation to find that:

∫02f(x) dx=lim⁡n→∞∑i=1n2n⋅(2e2i/n+1)\int_0^2f(x)\ dx=\lim_{n\to \infty}\sum_{i=1}^n \frac{2}{n}\cdot (2e^{2i/n}+1)

Practice Problem 3 Solution

Last question! Start by defining Δt\Delta t in terms of nn: 4−1n=3n\frac{4-1}{n}=\frac{3}{n}. Then, do the same for tit_i: ti=a+Δt⋅i=1+3nit_i=a+\Delta t\cdot i=1+\frac{3}{n}i. Then, plug this in to v(t)v(t) to get:

v(ti)=2(1+3ni)+1=2+6ni+1=6ni+3v(t_i)=2\Big(1+\frac{3}{n}i\Big)+1=2+\frac{6}{n}i+1=\frac{6}{n}i+3

Finally, plug this all into the general limit equation to find that:

∫14v(t) dt=lim⁡n→∞∑i=1n3n⋅(6ni+3)\int_1^4v(t)\ dt=\lim_{n\to \infty}\sum_{i=1}^n \frac{3}{n}\cdot \Big(\frac{6}{n}i+3\Big)

💫 Closing

Now that you’ve completed this guide, you should feel comfortable expressing Riemann sums using summation notation, understand the connection between definite integrals and Riemann sums, and be able to rewrite a definite integral as the limit of a Riemann sum! 🏃

Vocabulary

The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.

TermDefinition
continuousA function that has no breaks, jumps, or holes in its graph over a given interval.
definite integralThe integral of a function over a specific interval [a, b], representing the net signed area between the curve and the x-axis.
limitThe value that a function approaches as the input approaches some value, which may or may not equal the function's value at that point.
limiting caseThe value or behavior that a mathematical expression approaches as a parameter (such as the width of subintervals) approaches zero.
partitionA division of an interval into subintervals used to construct a Riemann sum.
Riemann sumA sum of the form ∑f(x_i*)Δx_i used to approximate the area under a curve by dividing the interval into subintervals and summing the areas of rectangles.
subintervalOne of the smaller intervals created by dividing a larger interval [a,b] into n parts.

Frequently Asked Questions

How do I calculate a Riemann sum step by step?

Step-by-step: pick f, interval [a,b], and how many subintervals n (or plan to let n → ∞). 1. Partition: Δx = (b−a)/n. Subintervals: [x0,x1],…,[x_{n-1},x_n] where x_i = a + iΔx. 2. Choose sample points x_i* in each subinterval: left (x_{i-1}), right (x_i), or midpoint ( (x_{i-1}+x_i)/2 ). This is your sample rule. 3. Form each rectangle area: f(x_i*)·Δx. 4. Sum: R_n = Σ_{i=1}^{n} f(x_i*) Δx (sigma notation). That’s a Riemann sum (CED LIM-5.B.2). 5. Approximate area/accumulation by computing R_n for a chosen n (increase n for better accuracy). 6. Definite integral = limiting case: ∫_a^b f(x) dx = lim_{n→∞} Σ_{i=1}^n f(x_i*) Δx (CED LIM-5.C.1). If the limit exists, it equals the exact accumulated value. Quick tip: on the AP exam, show Δx, x_i formula, sigma form, and state the limit when you convert a Riemann sum to an integral. For extra practice, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).

What's the formula for left, right, and midpoint Riemann sums?

If you partition [a,b] into n equal subintervals with Δx = (b−a)/n and xi = a + iΔx, then the Riemann-sum formulas are: - Left Riemann sum: Ln = Σ_{i=0}^{n−1} f(xi) Δx (use left endpoints xi) - Right Riemann sum: Rn = Σ_{i=1}^{n} f(xi) Δx (use right endpoints xi) - Midpoint Riemann sum: Mn = Σ_{i=1}^{n} f(xi*) Δx where xi* = a + (i−½)Δx (midpoint of ith subinterval) As n → ∞ (and max Δx_i → 0), any of these sums (with appropriate sample points) can converge to the definite integral: ∫_a^b f(x) dx = lim_{n→∞} Σ_{i=1}^{n} f(xi*) Δx. These are exactly what the CED calls Riemann sums and their limiting case gives the definite integral (LIM-5.C.1/C.2). For a short study guide walkthrough see the Topic 6.3 Fiveable guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX). For lots of practice problems, check Fiveable practice (https://library.fiveable.me/practice/ap-calculus).

When do I use left vs right vs midpoint Riemann sums and does it matter?

Use left, right, or midpoint when you pick the sample point x_i* in each subinterval of a Riemann sum. Practically: - Left Riemann sum: pick left endpoint of each subinterval. If f is decreasing on [a,b], left sums overestimate; if increasing, they underestimate. - Right Riemann sum: pick right endpoint. Opposite over/under behavior from left. - Midpoint Riemann sum: pick the midpoint. For the same number of equal-width subintervals, midpoint is usually more accurate (error often smaller) because positive and negative local errors cancel more. Does it matter? For a finite n it can change the approximation and whether it’s an over/under estimate. But in the limiting case (max Δx → 0)—which is what the CED emphasizes (LIM-5.C.1 & LIM-5.C.2)—any choice of sample points that stays inside each subinterval gives the same definite integral if f is continuous. On the AP exam, you might be asked to write an integral as a limit of left/right/midpoint sums or to judge over/under estimates—practice all three (see the Topic 6.3 study guide: https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX). For more practice problems, check Fiveable’s AP Calc practice set (https://library.fiveable.me/practice/ap-calculus).

What's the difference between a Riemann sum and a definite integral?

A Riemann sum is an approximation: you pick a partition of [a,b], choose sample points x_i* in each subinterval, and add f(x_i*)·Δx_i (left, right, or midpoint). A definite integral is the limit of those approximations as the maximum subinterval width → 0. In CED language (LIM-5.B and LIM-5.C): ∫_a^b f(x) dx = lim_{max Δx_i→0} Σ_{i=1}^n f(x_i*)Δx_i. So think: Riemann sums = finite sums that approximate area; the definite integral = the exact area obtained by taking the limit. On the AP exam you’ll be asked to set up sums in sigma notation and recognize or evaluate their limits as integrals (Topic 6.3). For a focused review, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX). For broader unit review and lots of practice problems, check the Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6) and the practice bank (https://library.fiveable.me/practice/ap-calculus).

I don't understand how Riemann sums turn into definite integrals - can someone explain?

Think of a Riemann sum as a precise recipe for approximating area: partition [a,b] into n subintervals, pick a sample point x_i* in each, and add up f(x_i*)·Δx_i. In sigma form that’s Σ_{i=1}^n f(x_i*)Δx_i. As you refine the partition (make the largest Δx_i → 0 and n → ∞), those rectangle sums settle to one number—the definite integral. Formally, ∫_a^b f(x) dx = lim_{max Δx_i→0} Σ_{i=1}^n f(x_i*)Δx_i. That limit is the exact signed area under f on [a,b] (if f is integrable/continuous). On the AP CED this is LIM-5.C: you should be able to translate a limit-of-sums into ∫ notation and vice versa. Practically, practice converting left/right/midpoint sums in sigma form into integrals—that’s a common MC/FR skill (see Topic 6.3 study guide for examples) (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX). For more practice problems, check the AP calculus practice bank (https://library.fiveable.me/practice/ap-calculus).

How do I write summation notation for a Riemann sum?

Write a Riemann sum in sigma notation like this: 1) Partition [a,b] into n equal subintervals: Δx = (b−a)/n. 2) Choose a sample point x_i* in the i-th subinterval (left: x_i* = a+(i−1)Δx, right: x_i* = a+iΔx, midpoint: x_i* = a+(i−½)Δx). 3) The Riemann sum is Σ_{i=1}^n f(x_i*) Δx. So for a right Riemann sum: Σ_{i=1}^n f(a + iΔx)·Δx. For the limiting (definite integral) form, use the CED formula (LIM-5.C.1): ∫_a^b f(x) dx = lim_{n→∞} Σ_{i=1}^n f(x_i*) Δx, where max Δx_i → 0. This matches AP goals: express area approximations with sigma notation and interpret the limit as a definite integral (see Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX)). For extra practice problems, check (https://library.fiveable.me/practice/ap-calculus).

What does the delta x mean in Riemann sum formulas?

Delta x (Δx or Δx_i) is the width of a subinterval in a partition of [a,b]. In a Riemann sum Σ f(x_i*) Δx_i each term f(x_i*) gives the function value at a sample point in the i-th subinterval and Δx_i multiplies that value to give the area of a thin rectangle approximating area under f on that subinterval (CED LIM-5.B.2). For an equal partition of n subintervals, Δx = (b − a)/n. In the limiting definition of the definite integral you let the largest subinterval width (the norm) → 0: ∫_a^b f(x) dx = lim_{max Δx_i → 0} Σ f(x_i*) Δx_i (CED LIM-5.C.1). Practically, Δx measures how fine your approximation is—smaller Δx → more rectangles → better approximation. For a quick review, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and more practice at (https://library.fiveable.me/practice/ap-calculus).

How do I find the limit of a Riemann sum as n approaches infinity?

Think of the Riemann sum limit as “turning a sum into area.” Steps you’ll use every time: 1. Identify the interval [a,b] and Δx = (b−a)/n. 2. Express the sample point x_i* in terms of i (left: a+(i−1)Δx, right: a+iΔx, midpoint: a+(i−½)Δx). 3. Rewrite the sum in sigma form as Σ f(x_i*) Δx. 4. Recognize the limit as n → ∞ gives the definite integral: lim Σ f(x_i*) Δx = ∫_a^b f(x) dx (CED LIM-5.C). Example: lim_{n→∞} Σ_{k=1}^n (4/n) sqrt(2+4k/n) → Δx=4/n, x_k=2+4k/n so it equals ∫_2^6 sqrt(x) dx. On the AP exam you may be asked to translate either way—practice writing Δx and x_i* clearly. For a quick review, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX). For more practice problems, go to (https://library.fiveable.me/practice/ap-calculus).

What's the difference between upper and lower Riemann sums?

Upper and lower Riemann sums are two ways of approximating the area under a curve using a partition of [a,b]. For each subinterval you multiply a rectangle height by the subinterval width Δx, but you choose the height differently: - Lower sum (Darboux lower sum): on each subinterval take the infimum (greatest lower bound) of f there. That gives the largest rectangle heights you can guarantee are ≤ f on each subinterval, so the lower sum underrates area. - Upper sum (Darboux upper sum): on each subinterval take the supremum (least upper bound) of f there. That overestimates area. Key facts for AP Calc (LIM-5.B/C): for any partition U(f,P) ≥ L(f,P). As you refine the partition (max Δx → 0), if the upper and lower sums converge to the same limit, that common value is the definite integral ∫_a^b f(x) dx—this is Riemann integrability. Left/right/midpoint Riemann sums are just specific sample-point choices (not necessarily sup/inf). For practice and a quick review, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and unit overview (https://library.fiveable.me/ap-calculus/unit-6). More practice problems are at (https://library.fiveable.me/practice/ap-calculus).

Can I use my calculator to find Riemann sums or do I have to do it by hand?

Short answer: you can use a calculator for Riemann-sum calculations when the exam permits it, but you should be ready to do them by hand and show the setup. Details: on the AP exam a graphing calculator is allowed only for Part I, Section B (the last 15 multiple-choice) and for Section II, Part A (2 free-response questions). Many Riemann-sum / definite-integral questions appear on the no-calculator parts, so the College Board expects you to be able to (a) write sums in sigma form, (b) set up left/right/midpoint Δx and x_i* correctly, and (c) evaluate a limit to recognize the definite integral (CED LIM-5.C). Use your calculator to compute numeric sums or evaluate limits only when the question is in a calculator-allowed section. Practice both ways: learn the symbolic setup and limit interpretation by hand, and use a graphing calculator to speed numeric approximations when allowed. For topic review and problems, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and lots of practice on Fiveable (https://library.fiveable.me/practice/ap-calculus).

How do I convert from summation notation to definite integral notation?

Think of a Riemann sum as a Riemann sum in words: “sum of f(sample point) × width.” To convert sigma notation to a definite integral, do these steps: 1. Identify Δx from the factor multiplied by the summand (often written as something like b−a over n). If the factor is m/n, set Δx = m/n. 2. Match the sample point x_i* to a linear expression in i. Write x_i* = a + i·Δx (or a + (i−1)Δx for left-endpoint sums, or a + (i−½)Δx for midpoints). That gives you a and b = a + nΔx. 3. Recognize the summand as f(x_i*)·Δx. Then the limit as n → ∞ of the sum equals ∫_a^b f(x) dx by LIM-5.C in the CED. Quick example: lim_{n→∞} Σ_{i=1}^n (√(2 + 4i/n))·(4/n). Here Δx = 4/n, x_i = 2 + 4i/n, so this equals ∫_2^6 √x dx. This is exactly the limiting Riemann-sum → definite-integral idea in the AP CED (LIM-5.B/C). For more practice and step-by-step examples, check the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6).

Why do we partition intervals when doing Riemann sums?

You partition the interval because you’re turning a hard-to-find exact area (or total accumulation) into lots of easy pieces you can add up. Each subinterval [x_{i-1}, x_i] gives a rectangle (height = f(x_i*) , width = Δx_i) so a Riemann sum is Σ f(x_i*)Δx_i—exactly the CED description (LIM-5.B.2). By making the partition finer (the norm, max Δx_i, → 0) those rectangle sums approach the true value; that limit is the definite integral ∫_a^b f(x) dx (LIM-5.C.1). Practically, partitioning lets you: (1) choose left/right/midpoint sample points to make approximations, (2) express sums compactly with sigma notation, and (3) translate an integral into a limit of sums for proofs or exact evaluation. This is what AP asks you to interpret/represent in Topic 6.3. For the official study guide and practice problems on this topic see Fiveable’s Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6). For more practice, try the 1000+ AP calc problems (https://library.fiveable.me/practice/ap-calculus).

What does it mean when they say "as the width of subintervals approaches 0"?

It means you make the partition of [a,b] finer and finer so every subinterval’s length Δx_i gets arbitrarily small—formally the norm (max Δx_i) → 0. Practically: you take more subintervals, each narrower, so your sample rectangles (left/right/midpoint or any x_i*) fit the curve better. The CED writes this as ∫_a^b f(x) dx = lim_{max Δx_i→0} Σ f(x_i*) Δx_i (LIM-5.C.1). If f is continuous that limit exists and equals the definite integral—the exact signed area under f. For AP problems, recognize phrases like “as the widths approach 0” mean you should translate a Riemann sum into the corresponding definite integral (or vice versa). For a quick review see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and try practice problems (https://library.fiveable.me/practice/ap-calculus).

How do I know how many rectangles to use in a Riemann sum problem?

You don’t pick “the” number of rectangles out of nowhere—the problem tells you or tells you what it wants: - If the problem gives n (or a partition), use that many rectangles. Compute Δx = (b−a)/n and sample points x_i* (left, right, midpoint, or specified) and form Σ f(x_i*)Δx. (CED LIM-5.B.2 language: partition, subinterval width, sample point.) - If the problem asks for the limiting case (translate a Riemann sum to a definite integral), you let n → ∞. Replace Σ f(x_i*)Δx by ∫_a^b f(x) dx (CED LIM-5.C.1 and LIM-5.C.2). - If you’re asked to approximate and n isn’t given, pick an n that balances accuracy and work (more rectangles → smaller max Δx and better accuracy). Use left/right/midpoint error behavior (midpoint often more accurate for smooth f). Example: on [2,6] with n=4, Δx=(6−2)/4=1 and x_i*=2,3,4,5 for a left sum. For AP practice and worked examples, see the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and more problems at Fiveable practice (https://library.fiveable.me/practice/ap-calculus).

I'm confused about what x_i* means in the Riemann sum formula - is it just any point in the interval?

Short answer: yes—x_i* is any sample point chosen inside the i-th subinterval, but how you pick it matters for the approximation and for writing the sum. More detail: given a partition of [a,b] into subintervals [x_{i-1}, x_i] with width Δx_i, each term in a Riemann sum is f(x_i*)·Δx_i where x_i* ∈ [x_{i-1},x_i]. Common choices are left endpoints (x_i* = x_{i-1}), right endpoints (x_i* = x_i), or midpoints. For the definite integral, you take the limit as the norm (max Δx_i) → 0: if f is integrable, any choice of x_i* in each subinterval gives the same limit ∫_a^b f(x) dx. That idea is exactly LIM-5.C.1/C.2 in the CED. If you want practice turning sums into integrals (or vice versa) or seeing how different sample points behave on coarse partitions, check the Topic 6.3 study guide (https://library.fiveable.me/ap-calculus/unit-6/riemann-sums-summation-notation-definite-integral-notation/study-guide/RnM03H2k6l3ewvxX) and Fiveable’s AP Calc practice problems (https://library.fiveable.me/practice/ap-calculus).