Onto unit 6 of AP Calculus! If you were asked to calculate how many miles a car traveled in 3 hours moving at a constant speed of 65 miles per hour, how would you do it? Using this example, you’ll learn about Riemann sums, the basics of integral calculus, and how to apply it to real life!
🏎️ Change Over Time
Accumulation of change is exactly what it sounds like—the sum, over time, of how much something has changed. Let’s return to the example at the beginning: we want to know how far a car has traveled, and we are given its speed (in miles per hour) and the length of time it has been traveling. We want to know how many miles it has accumulated over 3 hours. This problem is fairly straightforward, and we can solve it with a simple equation:
where d is distance, v is velocity (speed), and t is time. Let’s apply it to the problem.
Notice that because we have the unit hours in the denominator of one term and the numerator of the other, they cancel, leaving us with just a unit of miles. This is how units will work for all of these problems—they should be the unit of the rate of change multiplied by the independent variable.
We’ve solved our first problem! Now, let’s connect it to calculus.

📈 Graphing Change Over Time
We can depict the relationship between how fast, how long, and how far the car traveled with a graph.

Here, we can see that the x-axis represents how long the car has been traveling and the y-axis represents how fast it is traveling. The shaded area under the curve represents the total distance traveled.
This example is about a car that is traveling at a constant speed, as though it was on the highway using cruise control. But in reality, a whole trip for a vehicle involves variation in speed. Let’s look at another example, where a car leaves its house, accelerates to 50 miles per hours, drives on the highway for almost two hours, decelerates to 20 miles per hour, finishes driving to its destination, and then decelerates to 0 miles per hour. How far did the car travel?

Based on our simpler example, we know that the shaded area under the curve will give us the distance the car traveled. But, we can’t just use the equation for an area of a rectangle here, because it’s a much more complex shape! The following piecewise function describes the curve:
There are a few different ways we can approach this problem: by estimating using rectangles, or by using an integral.
📊 Riemann Sums
The first way we can find area under the curve is by using something called a Riemann Sum. This involves drawing rectangles, or other easy shapes to take the area of, and using them to approximate the area under the curve. Let’s apply it to our problem!
✏️ Riemann Sum: Step-by-Step
Step 1: How Many Rectangles?
The first thing we need to do is decide how many rectangles we want to use to approximate our area under the curve. For simplicity’s sake, let’s just use six in this example. We want them to have equal widths, so we divide our total base by our number of rectangles. Since the car’s trip was three hours long, we’ll divide 3 by 6, to find a base length of 0.5.
Step 2: Graphing
Let’s add our six rectangles to our initial graph:

Step 3: Computation
Finally, let’s create a table and calculate the area of each rectangle. Our table of values looks like this:
| Base | Height |
|---|---|
| 0.5 | 0 |
| 0.5 | 50 |
| 0.5 | 50 |
| 0.5 | 50 |
| 0.5 | 50 |
| 0.5 | 20 |
To calculate the total area, we will sum the areas of each of these rectangles like so:
Since our base length is the same, we can factor it out and simplify our equation like this:
Therefore, using this simple approximation, we find that our car has traveled about 110 miles! However, based on the graph, we can see that this is probably somewhat inaccurate, as it includes both overestimations and underestimations of the true distance traveled. This is where integrals come in!
📈 Preview of Integrals
So far, we’ve worked on approximating the area under the curve, or the accumulation of change. But, we have a very powerful tool at our disposal—the integral. Integrals are also called anti-derivatives, which is exactly what it sounds like! They “undo” derivation, just like multiplication undoes division. They also calculate the exact area under the curve.
💡 Learn more about integrals starting in 6.7!
Integration is represented with the following notation:
This notation tells us to find the area under the curve for our function over the interval [0,3]. This type of integral is specifically called a definite integral. We won’t cover how to take the integral right now, but if you did take it, you would find that the exact area under the curve in our example problem is 117.44 miles.
📝 Practice
Let’s look at one final sample problem before trying it on your own!
Example Problem: Consider the following graph of the function , which represents the total distance traveled by a vehicle over time. What is the average speed of the vehicle?

Solution: Since this graph is composed entirely of straight lines, we can find the area of each composite shape geometrically. First, let’s draw the shapes we want to find the area of.
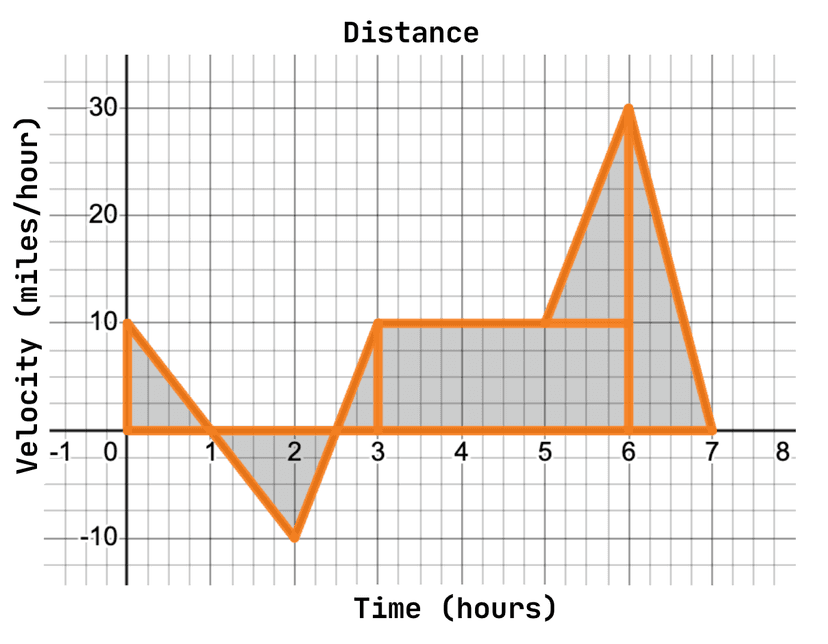
We can see that the first triangle has a base of 1 and a height of 10. Using the formula for the area of a triangle, , we find the area to be equal to 5 units. Our next triangle has a base of 1.5 and a height of -10. Applying the same formula, we find its area to be equal to -7.5 units. Importantly, this area is signed, meaning it is negative! In our example scenario, this would be like the car traveling in the opposite direction of its destination.
Our next triangle has a base of 0.5 and a height of 10, for an area of 2.5 units. The large rectangle has a base of 3 and a height of 10, so applying the formula for the area of a rectangle, , we find its area to be equal to 30 units. The triangle sitting on top of it has a base of 1 and a height of 20, for an area of 10 units. Finally, the last triangle has a base of 1 and a height of 30, for an area of 15. Summing these areas, we find the total area under the curve to be:
We learned earlier that our units are the rate of change multiplied by the independent (x-axis) variable, so in this case, we multiply miles/hour by hours. This gives us a unit of miles. Therefore, our car traveled a total of 55 miles toward its destination.
➗ Practice Problems and Solutions
❓Problems
Problem 1: A 50-gallon bathtub is being filled at a constant rate of 10 gal/minute. How long until the bathtub is full?
Problem 2: What is the total, exact area under the curve of the following graph, computed geometrically?

Problem 3: What is the area beneath the curve estimated with a Riemann sum of the function using 5 rectangles?

💡 Solutions
Problem 1: In this problem, we are given the rate of change, and the end accumulation. We’re missing the “overtime” component. In our very first problem, we found our total accumulation by multiplying the rate of change by our time. So, we used an equation like this: , where is accumulation, is the rate of change, and is time. We can solve for like so: . Applying this to our problem we find that .
Problem 2: Our graph is comprised of three trapezoids. The formula for the area of a trapezoid is
Where andbh28u^2$$.
Problem 3: We first need to draw our rectangles:

Since our graph goes from 0 to 10 and we have five rectangles, we know that each will have a base length of 2. We can use the y-values for each rectangle to get their heights. Thus, we calculate the area to be:
⭐ Closing
After completing this guide, you should be familiar with accumulation of change* and how it is represented graphically. You should also feel comfortable applying some basic strategies for calculating accumulation of change over time, and should now be ready to learn more about Riemann sums and integrals!
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| accumulation of change | The total amount of change in a quantity over an interval, represented by the area between a rate of change function and the x-axis. |
| area under a curve | The region between the graph of a function and the x-axis over a specified interval, which represents the accumulation of change when the function is a rate of change. |
| rate of change | The measure of how quickly a quantity changes with respect to another variable, often time. |
Frequently Asked Questions
How do I find the area under a rate of change graph?
Think of the graph as a rate r(t) (units per unit time). The area between r(t) and the t-axis over [a,b] = the accumulation (net change) of the quantity from a to b, and is given by the definite integral ∫_a^b r(t) dt (Net Change Theorem). If r(t) ≥ 0 on [a,b], the area is positive (quantity increases); if r(t) ≤ 0, area is negative (quantity decreases). Units of the area = (unit of r) × (unit of t). How to find it in practice: - If you can integrate r(t), compute an antiderivative R and evaluate R(b) − R(a). - If r(t) is simple shapes, use geometry (rectangles/triangles). - If you only have a graph, estimate signed area (use Riemann sums or count geometric pieces). - To get total distance (not net change) integrate |r(t)|. This is exactly what Topic 6.1/CED CHA-4.A tests—for a quick study guide check (and practice problems) see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and find hundreds of practice problems at (https://library.fiveable.me/practice/ap-calculus).
What's the difference between rate of change and accumulation of change?
Rate of change tells you how something is changing at each instant (like velocity v(t) in m/s)—it’s the derivative. Accumulation of change is the total change over an interval; you get it by finding the area between the rate-of-change graph and the x-axis (the definite integral). So ∫_a^b rate(t) dt = net change from a to b (signed area). If the rate is positive the accumulation is positive; if negative, accumulation is negative (signed area). Units: (unit of rate) × (unit of time) (CED CHA-4.A.4). Quick examples: velocity v(t) is a rate; ∫ v(t) dt gives displacement (net change). If you want total distance traveled, integrate |v(t)| (sum of positive areas). You can sometimes compute accumulation by geometry (triangles, rectangles) when the rate graph is simple (CED CHA-4.A.2). For more practice, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and lots of problems at (https://library.fiveable.me/practice/ap-calculus).
When do I use geometry vs integration to find accumulated change?
Use geometry when the region under the rate-of-change graph is made of standard shapes (rectangles, triangles, semicircles) whose areas you can compute exactly. In those cases CHA-4.A.2 applies: you can find accumulation (net change) by summing geometric areas—remembering signed area (above x-axis positive, below negative) and units (rate unit × time unit). Use integration (definite integrals or antiderivatives) when the rate function isn’t piecewise-linear or isn’t composed of simple shapes. The Net Change Theorem/FTC tells you ∫_a^b r(t) dt gives the accumulated change; if r changes sign, interpret as signed (net) change vs. total distance (use |r| if asked). If the graph is complex, partition the interval into subintervals you can handle (geometric parts or numerical sums), or evaluate the integral analytically/numerically. For AP tasks, expect geometry on graph-based multiple-choice/free-response but be ready to set up and evaluate integrals (Unit 6 focus). For quick review and practice, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and practice problems (https://library.fiveable.me/practice/ap-calculus).
I don't understand how area under a curve gives me total change - can someone explain?
Think of the graph as a rate-of-change function (like velocity v(t) in meters per second). The area between v(t) and the t-axis over [a,b] sums up tiny changes v(t)·Δt (speed × tiny time)—that sum (a Riemann sum) becomes the definite integral ∫[a,b] v(t) dt. By the Net Change Theorem, that integral equals the total (net) change in the original quantity: position(b) − position(a). If the rate is positive the area adds; if negative the area subtracts (signed area). Units come from rate × independent variable (m/s × s = m). Sometimes you can get that area exactly by geometry (rectangles/triangles) per CHA-4.A. Note: ∫ gives net change (displacement); to get total distance you integrate the absolute value of the rate. For AP review and practice problems on this topic, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and the Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6).
What does it mean when the rate of change is negative and how does that affect the area?
If the rate of change (the function you’d integrate) is negative on an interval, it means the quantity is decreasing there—the accumulated change over that interval is negative. In terms of area: the region between the graph and the x-axis lies below the axis and contributes “negative signed area” to the definite integral. So ∫[a to b] r(t) dt gives the net change (positive area above minus area below). Practical notes for AP: this is exactly CHA-4.A in the CED—positive rate → positive accumulation, negative rate → negative accumulation. Remember the difference between net change (integral, signed area) and total distance (integral of |velocity|, always positive). Always include units: area units = (unit of rate)·(unit of x). For more examples and AP-style practice, check the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and extra problems (https://library.fiveable.me/practice/ap-calculus).
How do I know what units to use when finding accumulation of change?
When you find an accumulation of change (area under a rate-of-change graph), the units are just “rate units × independent-variable units.” That’s the CED idea: area = accumulation (CHA-4.A.4). So if v(t) is in meters per second and t is in seconds, ∫ v(t) dt has units meters (m/s × s = m). If R(t) is vehicles per hour and t is hours, ∫ R(t) dt gives number of vehicles. If the rate can be negative, the integral gives net change (signed area); to get total amount traveled you’d integrate the absolute value (distance vs displacement). Quick checklist: (1) identify the units on the vertical axis (rate), (2) identify the units on the horizontal axis (time, distance, etc.), (3) multiply them and include “per” cancellation (e.g., ounces/min × min = ounces). For more practice and AP-aligned examples see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6). For extra practice try the AP problem set (https://library.fiveable.me/practice/ap-calculus).
Can someone walk me through finding accumulated change step by step?
Accumulated change = the net area under a rate function. Step-by-step: 1. Identify the rate function r(t) and the interval [a,b]. Units: (rate unit)·(time unit) (CED CHA-4.A.4). 2. If r(t) is simple (lines, rectangles, triangles, semicircles), compute area by geometry and add signed areas above/below the x-axis (CHA-4.A.1–A.3). Positive r gives positive accumulation; negative r gives negative accumulation. 3. If not geometric, set up the definite integral: accumulated change = ∫_a^b r(t) dt (Net Change Theorem / Fundamental Theorem of Calculus). 4. If you need an exact antiderivative R(t), find R so R′(t)=r(t); then ∫_a^b r = R(b)−R(a). 5. For approximations use Riemann sums (left/mid/right) and note sign. On the AP exam you may be asked to interpret units or compare total distance vs. displacement (signed vs. absolute area). For worked examples and AP-style practice, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and thousands of practice problems (https://library.fiveable.me/practice/ap-calculus).
What's the formula for accumulation of change using areas?
The accumulation of change from a rate r(t) over [a,b] is the signed area under its graph—mathematically Δ = ∫_a^b r(t) dt. By the Net Change Theorem, if R(t) is a rate of change of some quantity F(t), then F(b) − F(a) = ∫_a^b R(t) dt. If R(t) ≥ 0 on [a,b] the integral equals the total (positive) accumulation; if R(t) changes sign it gives the net (signed) accumulation. Units: (units of rate) × (units of t) (CED CHA-4.A.4). When the rate is a simple shape you can evaluate the integral by geometry (sum of triangle/rectangle areas) (CED CHA-4.A.2). On the exam you’ll often set up a definite integral from a graph or compute area piecewise and give units (Topic 6.1/Unit 6). For extra practice and examples, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and practice problems (https://library.fiveable.me/practice/ap-calculus).
Why does multiplying rate units by time units give me the right answer?
Think of the rate as “how much per unit time.” Multiplying a rate by a time interval gives the amount that accumulates over that interval because rate × time = (amount/time) × time = amount. Example: if v(t)=30 miles/hour and you travel 2 hours, 30 mi/hr × 2 hr = 60 miles—that’s the accumulated distance. In calculus language (CED CHA-4.A): a tiny time slice Δt with rate r(t) produces a tiny change ≈ r(t)·Δt. Summing those slices (a Riemann sum) and taking the limit gives the definite integral ∫ r(t) dt, whose units are rate units × time units. If the rate is negative on an interval, the product (and the area) is negative—that gives signed accumulation (net change), not total distance. This is exactly the Net Change Theorem and the “area under a rate = accumulation” idea in Topic 6.1. For more examples and practice on units and accumulation, check the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) or try practice problems (https://library.fiveable.me/practice/ap-calculus).
I'm confused about when accumulated change is positive vs negative - help?
Think of accumulation as signed area: if the rate-of-change function (like v(t) or r(t)) is above the x-axis on an interval, the area between the graph and x-axis is positive so the accumulated change is positive; if the rate is below the axis, that area is negative so the accumulated change is negative. That’s exactly CHA-4.A (net change = area under rate). Quick examples: if v(t)>0 from t=a to b, displacement = ∫_a^b v(t) dt > 0 (you moved forward). If v(t)<0, ∫_a^b v(t) dt < 0 (net backward displacement). If you want total distance traveled, you need ∫_a^b |v(t)| dt (always positive)—signed area vs total distance. Always carry units: area’s units = (rate unit) × (time unit) per CHA-4.A.3–4. If you want practice identifying positive/negative accumulation from graphs or computing by geometry, check Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and try problems on the Unit 6 page (https://library.fiveable.me/ap-calculus/unit-6) or the practice set (https://library.fiveable.me/practice/ap-calculus).
How do I solve word problems about accumulation of change?
Word problems about accumulation of change are just area problems where the function given is a rate (like velocity, flow rate, people/hour). Steps you can use every time: 1. Identify the rate r(t) and the time interval [a,b]. The accumulated change = area between r(t) and the t-axis = definite integral ∫_a^b r(t) dt (net change theorem, CHA-4.A). Include units: (units of rate)×(time). 2. If r(t) is simple (constant, linear, triangular), use geometry to find area (CHA-4.A.2). If not, set up a definite integral. Use Riemann sums/midpoint/trapezoid to approximate when needed (Topic 6.2–6.3). 3. Watch sign: positive rate → positive accumulation; negative rate → negative accumulation (signed area). If the problem asks total distance, integrate |v(t)| instead of v(t). 4. Use the FTC to evaluate antiderivatives when possible (Topic 6.4). If data are tabular/graphical, partition the interval and sum areas of subregions (midpoint or trapezoid), and state units. For practice, study examples in the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and try problems at (https://library.fiveable.me/practice/ap-calculus).
What geometric shapes can I use to calculate areas under rate graphs?
You can often replace a messy rate graph with simple geometric shapes to get exact accumulations when the graph is made of straight lines or familiar curves—this is exactly what CHA-4.A.2 allows. Common shapes to use: - Rectangles: area = base × height. Useful for constant rates or Riemann sums (left/mid/right). - Trapezoids: area = (base)·(avg of parallel sides). Good when the top is a straight slant between two values. - Triangles: area = 1/2·base·height. Use for linear ramps that cross the axis. - Semicircles / quarter-circles: area = (πr²)/2 etc., when the rate matches part of a circle. - Composite shapes: combine the above (split intervals) for piecewise-linear or piecewise-geometric graphs. Remember signed area: areas below the x-axis count negative (CHA-4.A.3). Always keep units: (rate unit) × (time unit) gives the accumulation unit (CHA-4.A.4). If the region isn’t geometric, use definite integrals or Riemann sums (Topic 6.2–6.4). For a focused review, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and try practice problems (https://library.fiveable.me/practice/ap-calculus).
When the rate of change crosses the x-axis, how do I handle positive and negative areas?
When the rate r(t) crosses the x-axis, treat areas as signed: positive area (r>0) adds to accumulation, negative area (r<0) subtracts. Break the interval at each zero of r, compute the definite integral on each subinterval, and add them algebraically. Example: if r(t)>0 on [a,c] and r(t)<0 on [c,b], then net change = ∫_a^c r(t) dt + ∫_c^b r(t) dt (the second integral will be negative). If you need total distance (always positive), take absolute areas: total distance = ∫_a^c r(t) dt − ∫_c^b r(t) dt (or sum |∫subinterval r| over all pieces). Always attach units: units of r times units of t (CED CHA-4.A.4). This is exactly the Net Change Theorem and signed area idea tested in Topic 6.1—see the Topic 6.1 study guide for examples (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp). For more practice problems, check the AP Calculus practice page (https://library.fiveable.me/practice/ap-calculus).
I keep getting the wrong units for my accumulated change answers - what am I doing wrong?
You're almost always getting units wrong because you’re forgetting that the area (definite integral) combines the units of the rate with the units of the independent variable. From the CED (CHA-4.A.4): the unit for area = (unit of rate) × (unit of x). Quick checklist to fix it: - Identify the rate and its units (e.g., velocity = m/s, flow = L/min, vehicles/hour). - Identify the independent variable and its units (usually time in seconds/minutes/hours). - Multiply them: ∫ v(t) dt with v in m/s and t in s gives meters (m). Example: 3 m/s over 5 s → 3×5 = 15 m. - For Riemann sums: each rectangle area = (height unit)×(Δx unit)—same idea. - Watch signed vs total: ∫ v dt gives displacement (m); ∫ |v| dt gives total distance (m). The units are the same but the interpretation differs (CED: signed area, displacement vs total distance). - Also check you didn’t drop the differential (dx, dt)—that’s where the Δx unit comes from. This is exactly the kind of thing tested in Topic 6.1 (CHA-4.A) and on AP free-response questions that ask for units/interpretation. If you want more examples and practice problems, see the Topic 6.1 study guide (https://library.fiveable.me/ap-calculus/unit-6/integration-accumulation-change/study-guide/NWRV9MaRJO4Eno32l5Xp) and the Unit 6 overview (https://library.fiveable.me/ap-calculus/unit-6).