
2.2 Defining the Derivative of a Function and Using Derivative Notation
3 min read•february 15, 2024
Welcome back to AP Calculus with Fiveable! This topic focuses on determining derivative notation and calculating the derivative of a function. Let's combine our skills in calculating rates of change with the knowledge of limits to continue building our derivative skills. 🧱
↗️ Definition of Derivative
The derivative of a function at a single point is the instantaneous rate of change at that point. We learned how to calculate an instantaneous rate of change in the previous topic: Defining Average and Instantaneous Rates of Change at a Point.
But how can we find the derivative of the whole curve, instead of at just one single point? It would be far too tedious to calculate the instantaneous rate of change at every single point, and then graph. 🤔
We can actually find the derivative by generalizing the limit notation and not solving for the derivative at the point. Therefore, we use the limit definition of a derivative:
You will learn certain rules and shortcuts to calculating derivatives in the next few lessons, but for now, we will use the definition of the derivative to calculate the rate of change for a function.
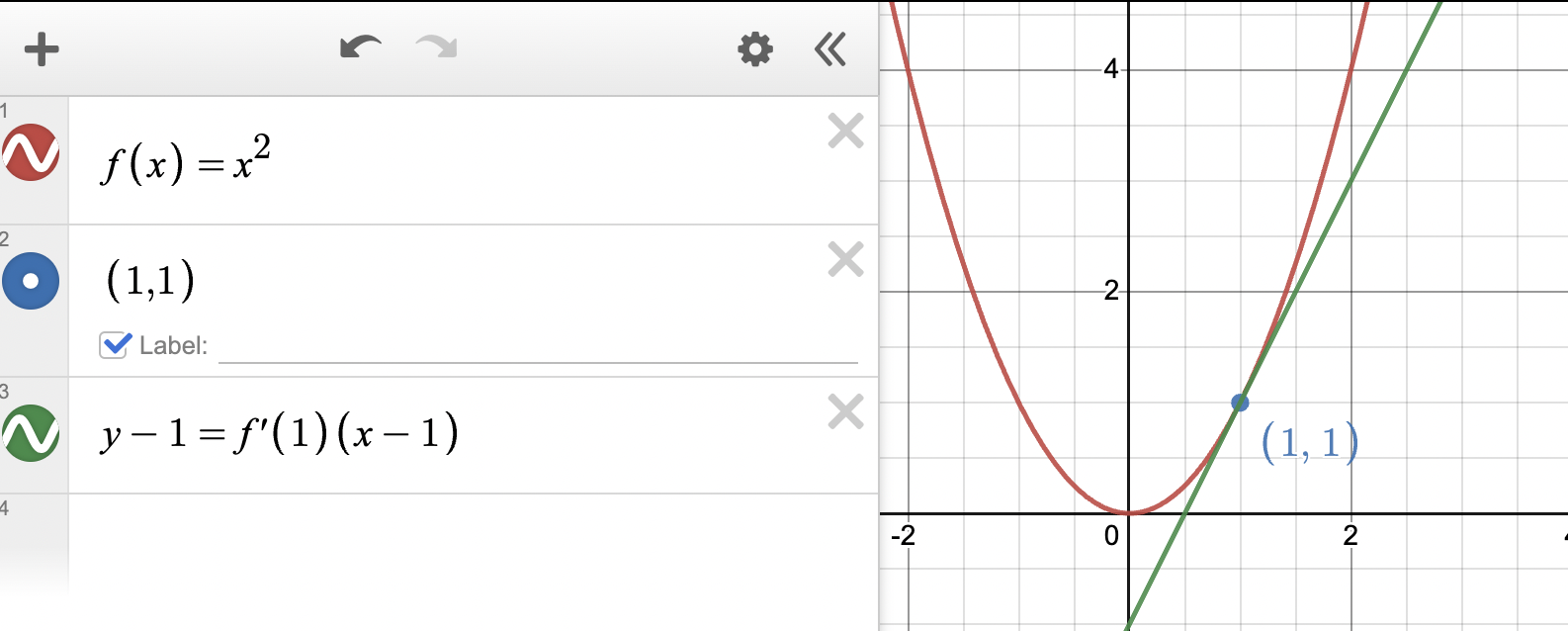
Graph created with Desmos
We can see that the slope of the tangent line is , or the derivative of when .
📝 Derivative Notation
There are several ways to represent a derivative in calculus.
If the original function can be represented as , then the derivative can be represented as , , or . These all describe the rate of change of the function as the dependent variable changes.
To reiterate,
They are all valid, and mean the same thing!
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Using the Definition of a Derivative
Given , calculate .
Let’s plug in all of the given information to the limit. Since ,
Let's simplify this so that we can take the limit and determine how the function changes. We can begin by expanding the numerator and then distributing it.
Now, let’s combine like terms.
We are almost there! Since , we can divide by .
As approaches , the middle term will approach . Therefore, we conclude:
Amazing work! 🎉
2) Tangent Line to a Curve
Given the curve , find the equation of the line tangent to the curve at .
Let’s use the definition of derivative to first calculate the derivative at .
This might seem a bit intimidating, but here we can change the two fractions in the numerator to have a common denominator.
In the numerator, we then have . Therefore…
Now, we can multiply the numerator by the reciprocal of the denominator.
Now let’s expand the numerator.
We can cancel the from both the numerator and the denominator to get
As approaches , the second term in the denominator will approach , so we can conclude
Now we need to write the equation of a tangent line! Remember that a line can be represented in point-slope form as the following: where is the slope, or the derivative at the point .
Our point is , so .
Now we have all of the necessary information to write the equation of the tangent line:
Great work! Let's check that this line is tangent to the curve at the point .
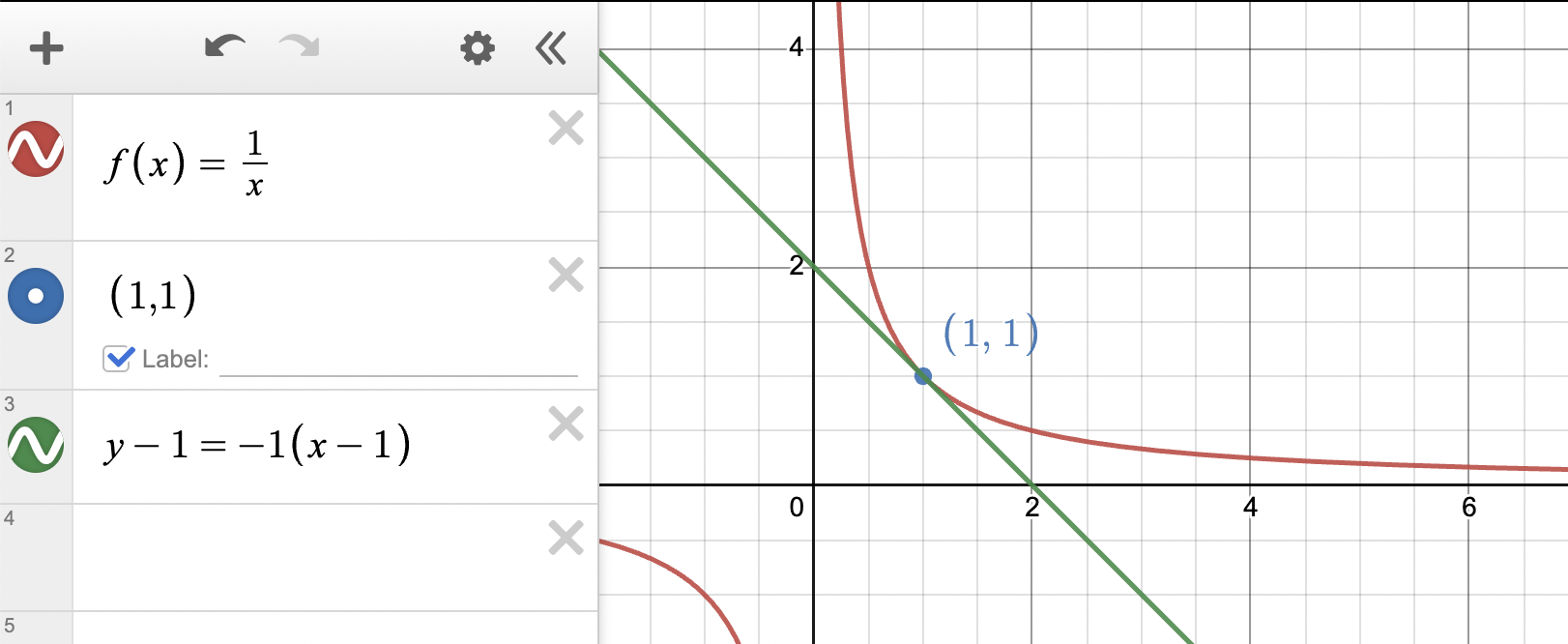
Graph created with Desmos
Looks great! 🙌
🌟 Closing
Great job! 🚀👩🚀 You're mastering these concepts, and with practice, you'll navigate derivatives and continuity with confidence. Determining derivatives and using different derivative notations are crucial skills in AP Calculus. As you encounter questions on the exam, remember to check for domain restrictions and assess piecewise continuity.

Image Courtesy of Giphy
Key Terms to Review (6)
Derivatives
: Derivatives are the rates at which quantities change. They measure how a function behaves as its input (x-value) changes.Difference Quotient
: The difference quotient measures the average rate at which a quantity changes over an interval by taking the difference between two points on a graph and dividing it by their corresponding x-values.f'(x)
: The derivative of a function f(x) represents the rate at which the function is changing at any given point. It measures the slope of the tangent line to the graph of the function.Slope
: The slope refers to the steepness of a line. It measures how much a line rises or falls for every unit it moves horizontally.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.Velocity
: Velocity is the rate at which an object's position changes with respect to time. It includes both speed and direction.2.2 Defining the Derivative of a Function and Using Derivative Notation
3 min read•february 15, 2024
Welcome back to AP Calculus with Fiveable! This topic focuses on determining derivative notation and calculating the derivative of a function. Let's combine our skills in calculating rates of change with the knowledge of limits to continue building our derivative skills. 🧱
↗️ Definition of Derivative
The derivative of a function at a single point is the instantaneous rate of change at that point. We learned how to calculate an instantaneous rate of change in the previous topic: Defining Average and Instantaneous Rates of Change at a Point.
But how can we find the derivative of the whole curve, instead of at just one single point? It would be far too tedious to calculate the instantaneous rate of change at every single point, and then graph. 🤔
We can actually find the derivative by generalizing the limit notation and not solving for the derivative at the point. Therefore, we use the limit definition of a derivative:
You will learn certain rules and shortcuts to calculating derivatives in the next few lessons, but for now, we will use the definition of the derivative to calculate the rate of change for a function.

Graph created with Desmos
We can see that the slope of the tangent line is , or the derivative of when .
📝 Derivative Notation
There are several ways to represent a derivative in calculus.
If the original function can be represented as , then the derivative can be represented as , , or . These all describe the rate of change of the function as the dependent variable changes.
To reiterate,
They are all valid, and mean the same thing!
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Using the Definition of a Derivative
Given , calculate .
Let’s plug in all of the given information to the limit. Since ,
Let's simplify this so that we can take the limit and determine how the function changes. We can begin by expanding the numerator and then distributing it.
Now, let’s combine like terms.
We are almost there! Since , we can divide by .
As approaches , the middle term will approach . Therefore, we conclude:
Amazing work! 🎉
2) Tangent Line to a Curve
Given the curve , find the equation of the line tangent to the curve at .
Let’s use the definition of derivative to first calculate the derivative at .
This might seem a bit intimidating, but here we can change the two fractions in the numerator to have a common denominator.
In the numerator, we then have . Therefore…
Now, we can multiply the numerator by the reciprocal of the denominator.
Now let’s expand the numerator.
We can cancel the from both the numerator and the denominator to get
As approaches , the second term in the denominator will approach , so we can conclude
Now we need to write the equation of a tangent line! Remember that a line can be represented in point-slope form as the following: where is the slope, or the derivative at the point .
Our point is , so .
Now we have all of the necessary information to write the equation of the tangent line:
Great work! Let's check that this line is tangent to the curve at the point .

Graph created with Desmos
Looks great! 🙌
🌟 Closing
Great job! 🚀👩🚀 You're mastering these concepts, and with practice, you'll navigate derivatives and continuity with confidence. Determining derivatives and using different derivative notations are crucial skills in AP Calculus. As you encounter questions on the exam, remember to check for domain restrictions and assess piecewise continuity.

Image Courtesy of Giphy
Key Terms to Review (6)
Derivatives
: Derivatives are the rates at which quantities change. They measure how a function behaves as its input (x-value) changes.Difference Quotient
: The difference quotient measures the average rate at which a quantity changes over an interval by taking the difference between two points on a graph and dividing it by their corresponding x-values.f'(x)
: The derivative of a function f(x) represents the rate at which the function is changing at any given point. It measures the slope of the tangent line to the graph of the function.Slope
: The slope refers to the steepness of a line. It measures how much a line rises or falls for every unit it moves horizontally.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.Velocity
: Velocity is the rate at which an object's position changes with respect to time. It includes both speed and direction.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.