
1.3 Estimating Limit Values from Graphs
2 min read•february 15, 2024
In this guide, we're going to delve into the concept of estimating limit values from graphs. You’ll need to follow the path of functions and make conclusions on the limits occurring.
You’ll not only understand how to estimate the limits of functions from graphs, but you’ll also be able to recognize the opposite: when limits might not exist. Let’s get into it! ⬇️
🎯 Understanding the Concept of Limits
Before we dive into estimating limits from graphs, let's make sure we're on the same page about the concept of limits, including one-sided limits:
🚫 Limit: A limit is a fundamental concept in calculus that describes the behavior of a function as it approaches a particular point. We're often interested in understanding what value a function gets close to as it gets closer and closer to a specific x-value.
To quickly review how to define limits, check out Key Topic 1.2!
↔️ One-Sided Limits: Sometimes, we need to examine the behavior of a function as it approaches a point from one direction (left or right). These are called one-sided limits.
Here’s an example of a left-hand limit (approaching from the left side):
And here’s a right-hand limit (approaching from the right side):
📊 Estimating Limits from Graphs
Now, let's get to the heart of the matter: estimating limits from graphs. Graphical representations can be incredibly useful in gaining insights into the behavior of a function, and estimating limits is one of the skills you'll develop in AP Calculus AB.
🧙♂️ Tips and Tricks
When estimating limits from graphs…
- 👀 Visualize the Point: Look at the graph of the function near the point in question. Try to visualize what happens as you get closer to that x-value. Does the function seem to approach a specific y-value? If so, that's a good estimate of the limit.
- ✏️ Trace Along the Graph: You can trace the path of the graph as you approach the point. If the function appears to be getting closer and closer to a single y-value, that's a good indicator of the limit.
- ☑️ Check One-Sided Limits: Evaluate the one-sided limits if necessary. Look at the behavior of the function as you approach the point from the left and the right. If these one-sided limits match, you've likely found the limit. If they differ, the limit might not exist.
🚧 Challenges with Graphical Estimation
While estimating limits from graphs is a valuable skill, it's essential to recognize that graphical representations have their limitations. Here are a couple of challenges you may encounter:
⚖ Issues of Scale: Graphs can distort the actual behavior of a function due to scale. If the scale is not appropriately chosen, it may give a misleading impression of the limit. Always pay attention to the scale of the graph.
💼 Missed Function Behavior: Sometimes, a graph may miss important function behavior, especially if there are abrupt changes or discontinuities in the function that aren't visible on the graph. Be cautious of such cases.
❌ When Limits Might Not Exist
Understanding that limits might not exist for certain functions at particular values of x is crucial. Here are some scenarios where a limit might not exist:
Limit DNE: Unbounded Function
If the function grows without bound as x gets closer to a specific value, the limit does not exist, or DNE. Think of functions like 1/x as x approaches 0.
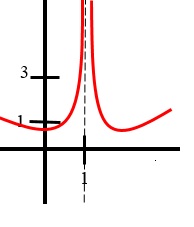
Image Courtesy of Study.com
Limit DNE: Oscillating Function
Some functions exhibit oscillatory behavior as they approach a point. In such cases, the limit does not exist, or DNE. For example, sin(1/x) as x approaches 0 oscillates wildly.

Image Courtesy of Study.com
Limit DNE: Left and Right Limits Differ
If the limit from the left and the limit from the right do not match, the overall limit doesn't exist, or DNE. This indicates a discontinuity at that point.

Image Courtesy of Study.com
📝Evaluating Limits: Practice Problems
Now that you have the information above, it’s time to test out your skills! Use the graph below to evaluate the following limits:
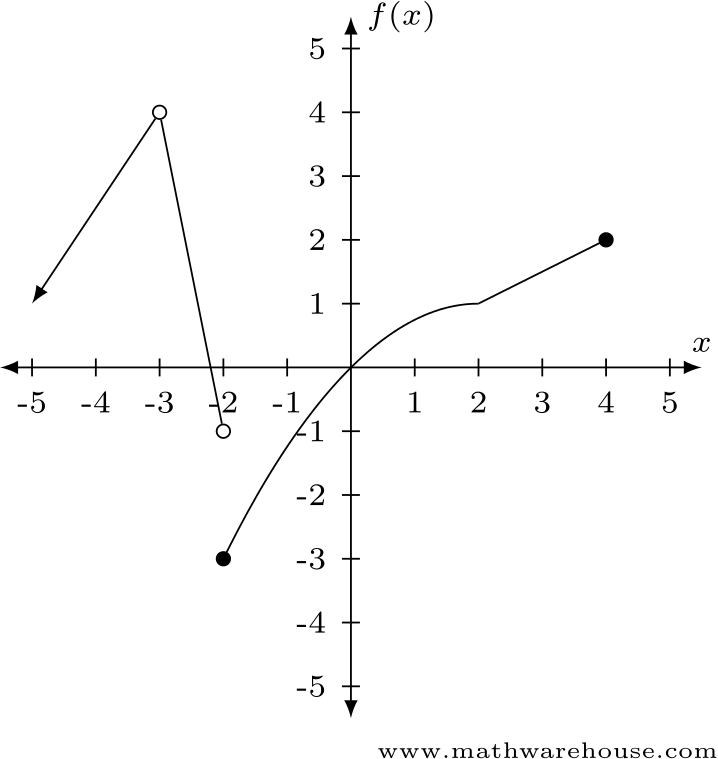
Image Courtesy of Mathwarehouse.com
✏️ Practice Problems: Answers
-
- , because as f(x) approaches 2 from the left side, the limit is -1.
- , because as f(x) approaches 2 from the right side, the limit is -3.
- Different limits from each side mean that the limit at the point, which is -2, doesn’t exist.
💫 Conclusion
Remember to visualize the point, trace along the graph, and check for one-sided limits. Be aware of the limitations of graphical representations and the situations in which limits might not exist. With these insights, you're well-prepared to tackle this aspect of calculus with confidence.
Keep practicing, and you'll master the art of estimating limits from graphs. Good luck! ☘️
1.3 Estimating Limit Values from Graphs
2 min read•february 15, 2024
In this guide, we're going to delve into the concept of estimating limit values from graphs. You’ll need to follow the path of functions and make conclusions on the limits occurring.
You’ll not only understand how to estimate the limits of functions from graphs, but you’ll also be able to recognize the opposite: when limits might not exist. Let’s get into it! ⬇️
🎯 Understanding the Concept of Limits
Before we dive into estimating limits from graphs, let's make sure we're on the same page about the concept of limits, including one-sided limits:
🚫 Limit: A limit is a fundamental concept in calculus that describes the behavior of a function as it approaches a particular point. We're often interested in understanding what value a function gets close to as it gets closer and closer to a specific x-value.
To quickly review how to define limits, check out Key Topic 1.2!
↔️ One-Sided Limits: Sometimes, we need to examine the behavior of a function as it approaches a point from one direction (left or right). These are called one-sided limits.
Here’s an example of a left-hand limit (approaching from the left side):
And here’s a right-hand limit (approaching from the right side):
📊 Estimating Limits from Graphs
Now, let's get to the heart of the matter: estimating limits from graphs. Graphical representations can be incredibly useful in gaining insights into the behavior of a function, and estimating limits is one of the skills you'll develop in AP Calculus AB.
🧙♂️ Tips and Tricks
When estimating limits from graphs…
- 👀 Visualize the Point: Look at the graph of the function near the point in question. Try to visualize what happens as you get closer to that x-value. Does the function seem to approach a specific y-value? If so, that's a good estimate of the limit.
- ✏️ Trace Along the Graph: You can trace the path of the graph as you approach the point. If the function appears to be getting closer and closer to a single y-value, that's a good indicator of the limit.
- ☑️ Check One-Sided Limits: Evaluate the one-sided limits if necessary. Look at the behavior of the function as you approach the point from the left and the right. If these one-sided limits match, you've likely found the limit. If they differ, the limit might not exist.
🚧 Challenges with Graphical Estimation
While estimating limits from graphs is a valuable skill, it's essential to recognize that graphical representations have their limitations. Here are a couple of challenges you may encounter:
⚖ Issues of Scale: Graphs can distort the actual behavior of a function due to scale. If the scale is not appropriately chosen, it may give a misleading impression of the limit. Always pay attention to the scale of the graph.
💼 Missed Function Behavior: Sometimes, a graph may miss important function behavior, especially if there are abrupt changes or discontinuities in the function that aren't visible on the graph. Be cautious of such cases.
❌ When Limits Might Not Exist
Understanding that limits might not exist for certain functions at particular values of x is crucial. Here are some scenarios where a limit might not exist:
Limit DNE: Unbounded Function
If the function grows without bound as x gets closer to a specific value, the limit does not exist, or DNE. Think of functions like 1/x as x approaches 0.

Image Courtesy of Study.com
Limit DNE: Oscillating Function
Some functions exhibit oscillatory behavior as they approach a point. In such cases, the limit does not exist, or DNE. For example, sin(1/x) as x approaches 0 oscillates wildly.

Image Courtesy of Study.com
Limit DNE: Left and Right Limits Differ
If the limit from the left and the limit from the right do not match, the overall limit doesn't exist, or DNE. This indicates a discontinuity at that point.

Image Courtesy of Study.com
📝Evaluating Limits: Practice Problems
Now that you have the information above, it’s time to test out your skills! Use the graph below to evaluate the following limits:

Image Courtesy of Mathwarehouse.com
✏️ Practice Problems: Answers
-
- , because as f(x) approaches 2 from the left side, the limit is -1.
- , because as f(x) approaches 2 from the right side, the limit is -3.
- Different limits from each side mean that the limit at the point, which is -2, doesn’t exist.
💫 Conclusion
Remember to visualize the point, trace along the graph, and check for one-sided limits. Be aware of the limitations of graphical representations and the situations in which limits might not exist. With these insights, you're well-prepared to tackle this aspect of calculus with confidence.
Keep practicing, and you'll master the art of estimating limits from graphs. Good luck! ☘️

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.