
7.9 Logistic Models with Differential Equations
4 min read•february 15, 2024
Besides exponential models, differential equations can also be used with logistic models. In this topic, we’ll cover what logistic models are and how differential equations are relevant to them.
📈 Logistic Models with Differential Equations
The logistic model or logistic growth model is a differential equation that describes how a population grows over time—it grows proportionally to its size but stops growing when it reaches a certain size. Specifically, the model states that the rate of change of a population is jointly proportional to the size of the population and the difference between the population and the carrying capacity. The carrying capacity is the maximum number of individuals that the environment can sustain. 🌵
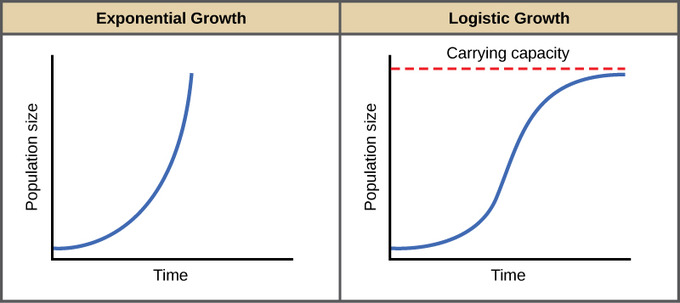
Image Courtesy of Biology LibreTexts
Mathematically, we have the following differential equation, where is the population, is a positive constant representing the growth rate, and is the carrying capacity.
An equivalent form is the following…
The logistic growth model is widely used in ecology, biology, and other fields to describe the growth of populations of animals, plants, and microorganisms. It can also be used to describe the growth of human populations and other quantities that have a carrying capacity.
For the AP exam, you should be able to determine the carrying capacity of a logistic differential equation and the value of the dependent variable in a logistic differential equation at the point when it is changing fastest.
✏️ Example of a Logistic Model
Let’s walk through an example problem to see how it’s done!
The population of germs in a petri dish satisfies the following logistic differential equation where is measured in hours and the initial population is .
-
What is the carrying capacity of the population?
-
What is the population’s size when it’s growing the fastest?
1) Solving for Carrying Capacity
When goes to infinity, approaches the carrying capacity—there is a horizontal asymptote at the carrying capacity. This means that no matter the initial condition, the population will stabilize at the carrying capacity.
Additionally, approaches 0. So to find the carrying capacity, we just need to find such that approaches 0.
There are two cases where equals 0—one where equals (which just means is ) and one where equals .
Thus, the carrying capacity is
An alternative way to solve for the carrying capacity is to rewrite the equation in the form where is the carrying capacity.
We can rewrite in this form by dividing by and multiply by .
Thus, we can see here that the carrying capacity is
2) Population Growth
The population’s size grows the fastest at the vertex of which is a downward quadratic equation with zeros at and the carrying capacity. Since the vertex is halfway between the two zeros, we just need to divide the carrying capacity by . Therefore, the point of fastest change occurs at…
We already figured out in the previous part that the carrying capacity is .
Thus, the population’s size when it’s growing the fastest is .
📝 Logistic Model Practice Problem
Now it’s time for you to do a practice problem! 🌟
The population of bacteria in a petri dish satisfies the logistic differential equation where is measured in hours and the initial population is .
-
What is the carrying capacity of the population?
-
What is the population’s size when it’s growing the fastest?
✅ Answers and Solutions
Make sure you give the question a try before scrolling!
1) Solving for Carrying Capacity
When goes to infinity, approaches the carrying capacity and approaches 0. So to find the carrying capacity, we just need to find such that approaches 0.
There are two cases where equals 0—one where equals (which just means is ) and one where equals .
Thus, the carrying capacity is .
2) Population Growth
Remember from the question we did together that the population’s size grows the fastest at…
We already figured out in the previous part that the carrying capacity is , so all we have to do is plug in.
Thus, the population’s size when it’s growing the fastest is .
✨ Closing
Great job! Remember that the logistic growth model is a type of differential equation used to describe a growth process that is self-limiting. Here is a quick summary of the points we covered in this guide:
- The term indicates that the growth rate is proportional to the current population size.
- The term implies that the growth rate decreases as approaches , the carrying capacity.
- When the initial population size is less than the carrying capacity (, the population will grow exponentially, as the population size is far from the carrying capacity. But, as approaches , the growth rate will decrease. Think of it as you’re approaching the highest limit.
- At , the growth stops ().
- As approaches infinity, approaches .
- The point at which the population is changing the fastest is where is half the carrying capacity, .
And…guess what? You made it to the end of unit seven! Here’s the start of unit eight if you want to get a head start. 🏃
Key Terms to Review (7)
Critical Point
: A critical point is a point on a function where the derivative is either zero or undefined. It represents a potential maximum, minimum, or inflection point.Exponential Growth
: Exponential growth refers to a rapid increase in quantity over time, where the rate of growth is proportional to the current value. It occurs when a quantity multiplies by a constant factor at regular intervals.Implicit Differentiation
: Implicit differentiation is a technique used to differentiate an equation implicitly without explicitly solving for one variable in terms of another.Logistic Differential Equations
: Logistic differential equations are a type of differential equation that models population growth or decay with a limiting factor. It takes into account both the rate of change and the carrying capacity of the population.Logistic Growth Model
: The logistic growth model is a mathematical equation that describes how a population grows over time when it is limited by resources. It takes into account both the exponential growth phase and the leveling off phase.Second Derivative
: The second derivative of a function represents the rate at which the slope of the original function is changing. It measures how the rate of change of the first derivative changes.System of Equations
: A system of equations refers to a set of two or more equations that are solved simultaneously to find the values of the variables that satisfy all the equations.7.9 Logistic Models with Differential Equations
4 min read•february 15, 2024
Besides exponential models, differential equations can also be used with logistic models. In this topic, we’ll cover what logistic models are and how differential equations are relevant to them.
📈 Logistic Models with Differential Equations
The logistic model or logistic growth model is a differential equation that describes how a population grows over time—it grows proportionally to its size but stops growing when it reaches a certain size. Specifically, the model states that the rate of change of a population is jointly proportional to the size of the population and the difference between the population and the carrying capacity. The carrying capacity is the maximum number of individuals that the environment can sustain. 🌵

Image Courtesy of Biology LibreTexts
Mathematically, we have the following differential equation, where is the population, is a positive constant representing the growth rate, and is the carrying capacity.
An equivalent form is the following…
The logistic growth model is widely used in ecology, biology, and other fields to describe the growth of populations of animals, plants, and microorganisms. It can also be used to describe the growth of human populations and other quantities that have a carrying capacity.
For the AP exam, you should be able to determine the carrying capacity of a logistic differential equation and the value of the dependent variable in a logistic differential equation at the point when it is changing fastest.
✏️ Example of a Logistic Model
Let’s walk through an example problem to see how it’s done!
The population of germs in a petri dish satisfies the following logistic differential equation where is measured in hours and the initial population is .
-
What is the carrying capacity of the population?
-
What is the population’s size when it’s growing the fastest?
1) Solving for Carrying Capacity
When goes to infinity, approaches the carrying capacity—there is a horizontal asymptote at the carrying capacity. This means that no matter the initial condition, the population will stabilize at the carrying capacity.
Additionally, approaches 0. So to find the carrying capacity, we just need to find such that approaches 0.
There are two cases where equals 0—one where equals (which just means is ) and one where equals .
Thus, the carrying capacity is
An alternative way to solve for the carrying capacity is to rewrite the equation in the form where is the carrying capacity.
We can rewrite in this form by dividing by and multiply by .
Thus, we can see here that the carrying capacity is
2) Population Growth
The population’s size grows the fastest at the vertex of which is a downward quadratic equation with zeros at and the carrying capacity. Since the vertex is halfway between the two zeros, we just need to divide the carrying capacity by . Therefore, the point of fastest change occurs at…
We already figured out in the previous part that the carrying capacity is .
Thus, the population’s size when it’s growing the fastest is .
📝 Logistic Model Practice Problem
Now it’s time for you to do a practice problem! 🌟
The population of bacteria in a petri dish satisfies the logistic differential equation where is measured in hours and the initial population is .
-
What is the carrying capacity of the population?
-
What is the population’s size when it’s growing the fastest?
✅ Answers and Solutions
Make sure you give the question a try before scrolling!
1) Solving for Carrying Capacity
When goes to infinity, approaches the carrying capacity and approaches 0. So to find the carrying capacity, we just need to find such that approaches 0.
There are two cases where equals 0—one where equals (which just means is ) and one where equals .
Thus, the carrying capacity is .
2) Population Growth
Remember from the question we did together that the population’s size grows the fastest at…
We already figured out in the previous part that the carrying capacity is , so all we have to do is plug in.
Thus, the population’s size when it’s growing the fastest is .
✨ Closing
Great job! Remember that the logistic growth model is a type of differential equation used to describe a growth process that is self-limiting. Here is a quick summary of the points we covered in this guide:
- The term indicates that the growth rate is proportional to the current population size.
- The term implies that the growth rate decreases as approaches , the carrying capacity.
- When the initial population size is less than the carrying capacity (, the population will grow exponentially, as the population size is far from the carrying capacity. But, as approaches , the growth rate will decrease. Think of it as you’re approaching the highest limit.
- At , the growth stops ().
- As approaches infinity, approaches .
- The point at which the population is changing the fastest is where is half the carrying capacity, .
And…guess what? You made it to the end of unit seven! Here’s the start of unit eight if you want to get a head start. 🏃
Key Terms to Review (7)
Critical Point
: A critical point is a point on a function where the derivative is either zero or undefined. It represents a potential maximum, minimum, or inflection point.Exponential Growth
: Exponential growth refers to a rapid increase in quantity over time, where the rate of growth is proportional to the current value. It occurs when a quantity multiplies by a constant factor at regular intervals.Implicit Differentiation
: Implicit differentiation is a technique used to differentiate an equation implicitly without explicitly solving for one variable in terms of another.Logistic Differential Equations
: Logistic differential equations are a type of differential equation that models population growth or decay with a limiting factor. It takes into account both the rate of change and the carrying capacity of the population.Logistic Growth Model
: The logistic growth model is a mathematical equation that describes how a population grows over time when it is limited by resources. It takes into account both the exponential growth phase and the leveling off phase.Second Derivative
: The second derivative of a function represents the rate at which the slope of the original function is changing. It measures how the rate of change of the first derivative changes.System of Equations
: A system of equations refers to a set of two or more equations that are solved simultaneously to find the values of the variables that satisfy all the equations.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.