
6.12 Integrating Using Linear Partial Fractions
3 min read•february 15, 2024
Catherine Liu
Jed Quiaoit
Catherine Liu
Jed Quiaoit
So you might be thinking that a BC-only technique for integration is extremely difficult, but worry no more, linear partial fractions are here to help you! Personally, this was my favorite integration technique throughout the unit and is the most time-saving.
🤔 Understanding Partial Fraction Decomposition
In essence, partial fraction decomposition involves breaking down a fraction with a polynomial numerator and denominator into a sum of simpler fractions. This process relies on the fact that any rational function with a polynomial numerator and denominator can be expressed as a sum of partial fractions. The process transforms a complex fraction into a sum of simpler fractions, making it easier to integrate.
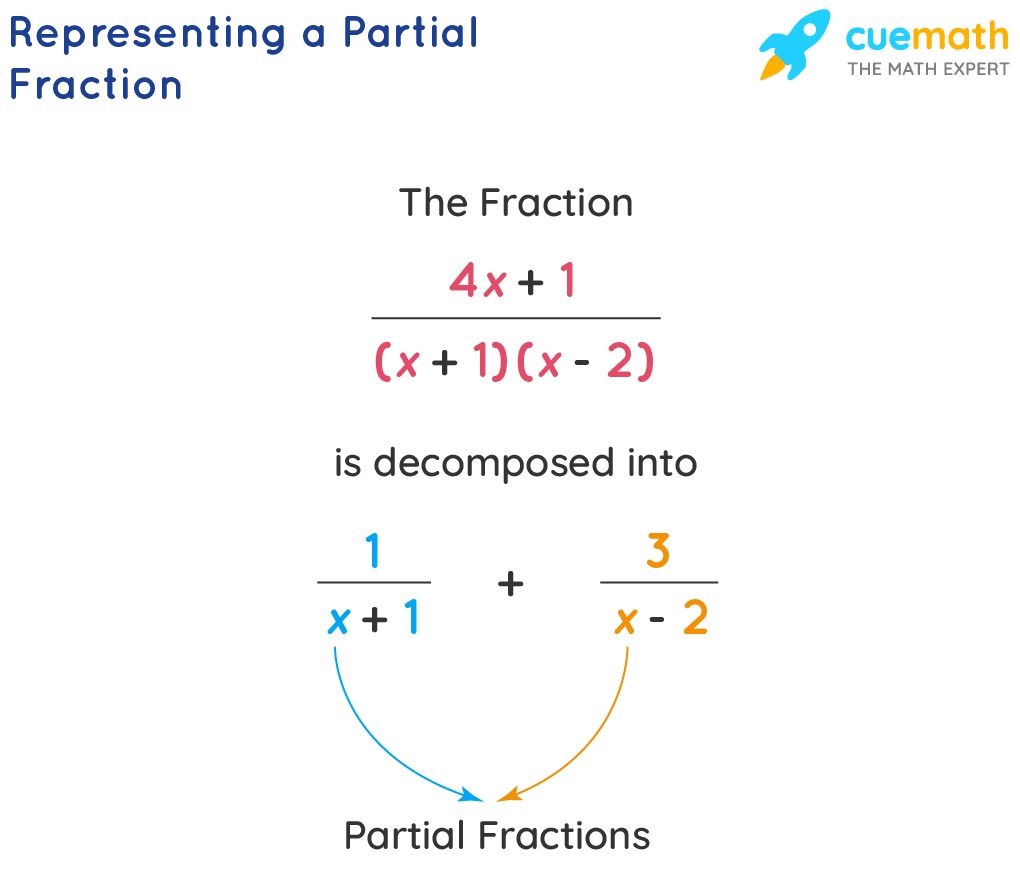
Image Courtesy of Cuemath
To begin, we first need to factor the denominator of the rational function into its distinct linear factors. If the denominator is not factorable, we can use long division to convert the rational function into a polynomial plus a remainder, in which the remainder is divided by a factorable denominator.
Next, we use the method of undetermined coefficients to find the coefficients of the partial fraction decomposition. This involves setting up a system of equations by multiplying both sides of the decomposition by the denominator and equating it to the original function. Then we solve this system of equations to find the coefficients.
🪜 Steps to Using Partial Fraction Decomposition
Before we get into an example, here are the steps we are going to use:
- Determine if the integrated is a rational function with linear, non-repeating factors in the denominator. This tells us we should use PFD as the technique for integrating.
- Split the rational function into several different functions.
- Multiply both sides of the equation by the common denominator.
- Solve for each variable in the numerators by picking values of to plug into the equation that cancels the other terms.
- Plug A, B, C, etc. back into the original equation and integrate each of the fractions separately.
There you go! Let’s put these steps into action. 🏃
🫣 Example of Partial Fraction Decomposition
Let’s walk through an example.
This is our function before we use this method to integrate. We are going to start by separating into two different fractions, including A and B as our stand-in numerators.
You can see that we separated the two fractions to make them two simpler fractions. Next, we will use cross-multiplication by the common denominator to clear the fractions. In this case, the common denominator is .
Now, we can solve for both of the variables, A and B. We do this by subbing in numbers for x to clear each of the variables at different times and figure out what the fractions are! Let’s start with solving for A. We are going to substitute 1 for x, to eliminate B as a variable.
Now we can do the same thing for B! Let’s substitute in .
With our newly solved values, we can incorporate them into the original split fraction to make the final problem that we are going to integrate.
And there you have it! An easy two-term expression to integrate quickly. If you need help with integrating this, check out our guide from topic 6.8. I find this a good reminder of how to use the reverse power rule to help with integration. But here is the final answer:
🧠 What if you have a non-factored fraction?
Out in the real world, you’re probably not going to have perfectly factored binomials with easy-to-use numbers. I know—I’m disappointed too. But luckily you are a mathematician with a full toolbox and you have lots of experience with factoring! You should be able to recognize a binomial that can be factored out evenly as well as expressions that will leave a remainder. It might sound silly, but you need to be on your A game with factoring because that can save you a lot of time on the test (and you need all the time you can get). ⏰
Let’s look at one more example: a denominator that has not yet been factored.
✏️ Example 2: PFD With Factorable Denominator
Consider the following function, .
Using your factoring skills, you should get:
Yay! A factored denominator! Let’s finish this problem following the same steps as with the last example.
Solving for A:
Solving for B:
Now we can integrate:
This gives us:
Great work! Now you have two examples under your belt. 👏
🧩 When Should Linear Partial Fractions be Used?
On any exam, you’ll just be given a function and asked to integrate. Well…when should you use this technique? 👀
The main thing you want to look for in your integral is a rational fraction. You want both your numerator and denominator to be polynomials and easy to work with. Your numerator should have a lower power than the denominator (the highest exponent in the numerator is lower than the highest exponent in the denominator). If this is not the case, you should probably consider another technique for integration.
Most importantly, practice practice practice! You will get the hang of it eventually. And if partial fractions aren’t your thing, that's no big deal! You can always find another way to integrate (although it might take longer). Good luck! 🍀
Key Terms to Review (5)
Integration
: Integration is an operation in calculus that finds antiderivatives, or reverse derivatives, allowing us to calculate areas, volumes, and other quantities related to curves and functions.Partial Fractions
: Breaking down a rational function into simpler fractions called partial fractions. This allows us to integrate complicated rational functions more easily.Rational Functions
: Rational functions are functions that can be expressed as a ratio (fraction) of two polynomials. They have both a numerator and denominator, where neither can be zero simultaneously.Synthetic Division
: Synthetic division is a method used to divide polynomials, specifically when dividing by a linear factor. It simplifies the process by using coefficients instead of variables.Undetermined Coefficients
: In calculus, undetermined coefficients is a method used to find the particular solution of a nonhomogeneous linear differential equation. It involves assuming that the particular solution can be expressed as a polynomial and then solving for the undetermined coefficients.6.12 Integrating Using Linear Partial Fractions
3 min read•february 15, 2024
Catherine Liu
Jed Quiaoit
Catherine Liu
Jed Quiaoit
So you might be thinking that a BC-only technique for integration is extremely difficult, but worry no more, linear partial fractions are here to help you! Personally, this was my favorite integration technique throughout the unit and is the most time-saving.
🤔 Understanding Partial Fraction Decomposition
In essence, partial fraction decomposition involves breaking down a fraction with a polynomial numerator and denominator into a sum of simpler fractions. This process relies on the fact that any rational function with a polynomial numerator and denominator can be expressed as a sum of partial fractions. The process transforms a complex fraction into a sum of simpler fractions, making it easier to integrate.

Image Courtesy of Cuemath
To begin, we first need to factor the denominator of the rational function into its distinct linear factors. If the denominator is not factorable, we can use long division to convert the rational function into a polynomial plus a remainder, in which the remainder is divided by a factorable denominator.
Next, we use the method of undetermined coefficients to find the coefficients of the partial fraction decomposition. This involves setting up a system of equations by multiplying both sides of the decomposition by the denominator and equating it to the original function. Then we solve this system of equations to find the coefficients.
🪜 Steps to Using Partial Fraction Decomposition
Before we get into an example, here are the steps we are going to use:
- Determine if the integrated is a rational function with linear, non-repeating factors in the denominator. This tells us we should use PFD as the technique for integrating.
- Split the rational function into several different functions.
- Multiply both sides of the equation by the common denominator.
- Solve for each variable in the numerators by picking values of to plug into the equation that cancels the other terms.
- Plug A, B, C, etc. back into the original equation and integrate each of the fractions separately.
There you go! Let’s put these steps into action. 🏃
🫣 Example of Partial Fraction Decomposition
Let’s walk through an example.
This is our function before we use this method to integrate. We are going to start by separating into two different fractions, including A and B as our stand-in numerators.
You can see that we separated the two fractions to make them two simpler fractions. Next, we will use cross-multiplication by the common denominator to clear the fractions. In this case, the common denominator is .
Now, we can solve for both of the variables, A and B. We do this by subbing in numbers for x to clear each of the variables at different times and figure out what the fractions are! Let’s start with solving for A. We are going to substitute 1 for x, to eliminate B as a variable.
Now we can do the same thing for B! Let’s substitute in .
With our newly solved values, we can incorporate them into the original split fraction to make the final problem that we are going to integrate.
And there you have it! An easy two-term expression to integrate quickly. If you need help with integrating this, check out our guide from topic 6.8. I find this a good reminder of how to use the reverse power rule to help with integration. But here is the final answer:
🧠 What if you have a non-factored fraction?
Out in the real world, you’re probably not going to have perfectly factored binomials with easy-to-use numbers. I know—I’m disappointed too. But luckily you are a mathematician with a full toolbox and you have lots of experience with factoring! You should be able to recognize a binomial that can be factored out evenly as well as expressions that will leave a remainder. It might sound silly, but you need to be on your A game with factoring because that can save you a lot of time on the test (and you need all the time you can get). ⏰
Let’s look at one more example: a denominator that has not yet been factored.
✏️ Example 2: PFD With Factorable Denominator
Consider the following function, .
Using your factoring skills, you should get:
Yay! A factored denominator! Let’s finish this problem following the same steps as with the last example.
Solving for A:
Solving for B:
Now we can integrate:
This gives us:
Great work! Now you have two examples under your belt. 👏
🧩 When Should Linear Partial Fractions be Used?
On any exam, you’ll just be given a function and asked to integrate. Well…when should you use this technique? 👀
The main thing you want to look for in your integral is a rational fraction. You want both your numerator and denominator to be polynomials and easy to work with. Your numerator should have a lower power than the denominator (the highest exponent in the numerator is lower than the highest exponent in the denominator). If this is not the case, you should probably consider another technique for integration.
Most importantly, practice practice practice! You will get the hang of it eventually. And if partial fractions aren’t your thing, that's no big deal! You can always find another way to integrate (although it might take longer). Good luck! 🍀
Key Terms to Review (5)
Integration
: Integration is an operation in calculus that finds antiderivatives, or reverse derivatives, allowing us to calculate areas, volumes, and other quantities related to curves and functions.Partial Fractions
: Breaking down a rational function into simpler fractions called partial fractions. This allows us to integrate complicated rational functions more easily.Rational Functions
: Rational functions are functions that can be expressed as a ratio (fraction) of two polynomials. They have both a numerator and denominator, where neither can be zero simultaneously.Synthetic Division
: Synthetic division is a method used to divide polynomials, specifically when dividing by a linear factor. It simplifies the process by using coefficients instead of variables.Undetermined Coefficients
: In calculus, undetermined coefficients is a method used to find the particular solution of a nonhomogeneous linear differential equation. It involves assuming that the particular solution can be expressed as a polynomial and then solving for the undetermined coefficients.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.