
9.1 Introducing Statistics: Do Those Points Align?
4 min read•january 8, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
As discussed in section 9.0, Unit 9 deals with and our ultimate question is how well our points from our sample align. In some cases, they align to a line; in other cases, possibly an exponential or quadratic equation. In AP Statistics, we primarily only focus on models. If they are not in a linear pattern, we know some techniques we can use to make our points better fit a linear pattern. (See Unit 2.9 for more background information as a refresher!) 🤩
Correlation
In our models, we are aiming at measuring the between the two variables based on our data set. One thing that is important to note is that sometimes may seem present, however, it is due to merely .
For instance, we can measure the inches of rain for every day and the number of the day of the month it was and plot the points with the day of the month on the x-axis and inches of rain on the y-axis. It is possible that we may see some sort of pattern that appears that the two things are correlated even though we know that is nonsense. This “” would be due to alone and not some sort of relationship between our two variables. 🌞
Also, it is so important to remember: does not mean !
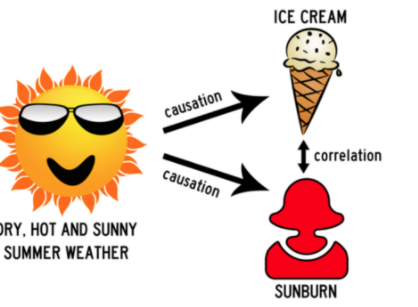
Causation
As we stressed in Unit 2, two variables may be correlated, but that does not establish a cause and effect relationship. As in the example above, a hot sunny day causes the ice cream to melt and it also causes sunburn. However, it would be silly to say that ice cream melting causes sunburn. The two things are correlated due to another variable: the hot sun (which influences ice cream consumption and sunburn).
Just like with any statistical study, it is wise to investigate any other variables that may be playing a part in your outcome. These variables are called . 😵💫
Repetition
A good scientific way to ensure that your results are not due to is to do two things:
Have a large for your data set.
Repeat the study in multiple populations with several large random samples.
For instance, consider the COVID-19 vaccine trials. When performing the clinical trials, it was imperative that they were using a large sample to randomly assign treatments. This ensured the safety of the vaccine across a broad scope but also reduced any in our pattern to a non-random , not just pure sampling variability between the placebo group and vaccine group.
Also, the same clinical trials were performed in multiple samples in various countries. This supports the effectiveness of the vaccines across multiple populations and strengthens the cause for vaccine administration around the globe. Yay for good news! 👏
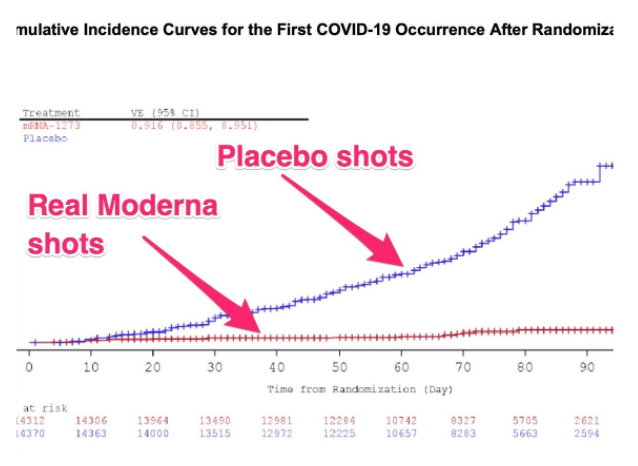
Image Taken From Business Insider
Variation in the World of Slopes
Variation in points’ positions relative to a theoretical line may be random or non-random. ⚠️
When the variation in the position of points relative to a theoretical line is random, it is called random error. This type of error is unpredictable and is due to factors that are beyond the control of the person conducting the experiment or making the measurement.
On the other hand, when the variation in the position of points relative to a theoretical line is non-random, it is called . This type of error is predictable and is due to factors that can be controlled, such as the accuracy of the measuring instrument or the technique used to make the measurement.

Source: Science Notes
Examples
Here are some examples of random error:
Fluctuations in the power supply while using an electronic balance to weigh an object
Temperature changes in the environment while conducting a chemical reaction
Wind gusts affecting the flight of a thrown object
And here are some examples of :
Using a ruler that is not made correctly to measure the length of an object
Using a thermometer that has not been calibrated to measure the temperature of a solution
Using a pipette that is not properly calibrated to dispense a precise volume of a liquid
🎥 Watch: AP Stats Unit 9 - Inference for Slopes
Key Terms to Review (8)
Causation
: Causation refers to a cause-and-effect relationship between two variables, where changes in one variable directly lead to changes in another variable.Confounding Variables
: Confounding variables are additional factors that are not accounted for in a study but can influence both the independent and dependent variables. They can lead to incorrect conclusions about cause-and-effect relationships.Correlation
: Correlation refers to the statistical measure of how two variables are related to each other. It indicates both the strength and direction of their relationship.Linear Regression
: Linear regression is a statistical method used to model the relationship between two variables by fitting a linear equation to observed data. It helps us understand how changes in one variable are associated with changes in another variable.Random Chance
: Random chance refers to the unpredictable variation that can occur in data due to natural variability or luck. It is the result of random events and cannot be controlled or predicted.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Scatterplots
: Scatterplots are graphs that display the relationship between two quantitative variables. Each point on the graph represents a pair of values, one for each variable.Systematic Error
: Systematic error refers to a consistent bias or deviation in the measurement process that affects the accuracy of data. It is not due to chance and can lead to results that are consistently higher or lower than the true value.9.1 Introducing Statistics: Do Those Points Align?
4 min read•january 8, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
As discussed in section 9.0, Unit 9 deals with and our ultimate question is how well our points from our sample align. In some cases, they align to a line; in other cases, possibly an exponential or quadratic equation. In AP Statistics, we primarily only focus on models. If they are not in a linear pattern, we know some techniques we can use to make our points better fit a linear pattern. (See Unit 2.9 for more background information as a refresher!) 🤩
Correlation
In our models, we are aiming at measuring the between the two variables based on our data set. One thing that is important to note is that sometimes may seem present, however, it is due to merely .
For instance, we can measure the inches of rain for every day and the number of the day of the month it was and plot the points with the day of the month on the x-axis and inches of rain on the y-axis. It is possible that we may see some sort of pattern that appears that the two things are correlated even though we know that is nonsense. This “” would be due to alone and not some sort of relationship between our two variables. 🌞
Also, it is so important to remember: does not mean !

Causation
As we stressed in Unit 2, two variables may be correlated, but that does not establish a cause and effect relationship. As in the example above, a hot sunny day causes the ice cream to melt and it also causes sunburn. However, it would be silly to say that ice cream melting causes sunburn. The two things are correlated due to another variable: the hot sun (which influences ice cream consumption and sunburn).
Just like with any statistical study, it is wise to investigate any other variables that may be playing a part in your outcome. These variables are called . 😵💫
Repetition
A good scientific way to ensure that your results are not due to is to do two things:
Have a large for your data set.
Repeat the study in multiple populations with several large random samples.
For instance, consider the COVID-19 vaccine trials. When performing the clinical trials, it was imperative that they were using a large sample to randomly assign treatments. This ensured the safety of the vaccine across a broad scope but also reduced any in our pattern to a non-random , not just pure sampling variability between the placebo group and vaccine group.
Also, the same clinical trials were performed in multiple samples in various countries. This supports the effectiveness of the vaccines across multiple populations and strengthens the cause for vaccine administration around the globe. Yay for good news! 👏

Image Taken From Business Insider
Variation in the World of Slopes
Variation in points’ positions relative to a theoretical line may be random or non-random. ⚠️
When the variation in the position of points relative to a theoretical line is random, it is called random error. This type of error is unpredictable and is due to factors that are beyond the control of the person conducting the experiment or making the measurement.
On the other hand, when the variation in the position of points relative to a theoretical line is non-random, it is called . This type of error is predictable and is due to factors that can be controlled, such as the accuracy of the measuring instrument or the technique used to make the measurement.

Source: Science Notes
Examples
Here are some examples of random error:
Fluctuations in the power supply while using an electronic balance to weigh an object
Temperature changes in the environment while conducting a chemical reaction
Wind gusts affecting the flight of a thrown object
And here are some examples of :
Using a ruler that is not made correctly to measure the length of an object
Using a thermometer that has not been calibrated to measure the temperature of a solution
Using a pipette that is not properly calibrated to dispense a precise volume of a liquid
🎥 Watch: AP Stats Unit 9 - Inference for Slopes
Key Terms to Review (8)
Causation
: Causation refers to a cause-and-effect relationship between two variables, where changes in one variable directly lead to changes in another variable.Confounding Variables
: Confounding variables are additional factors that are not accounted for in a study but can influence both the independent and dependent variables. They can lead to incorrect conclusions about cause-and-effect relationships.Correlation
: Correlation refers to the statistical measure of how two variables are related to each other. It indicates both the strength and direction of their relationship.Linear Regression
: Linear regression is a statistical method used to model the relationship between two variables by fitting a linear equation to observed data. It helps us understand how changes in one variable are associated with changes in another variable.Random Chance
: Random chance refers to the unpredictable variation that can occur in data due to natural variability or luck. It is the result of random events and cannot be controlled or predicted.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Scatterplots
: Scatterplots are graphs that display the relationship between two quantitative variables. Each point on the graph represents a pair of values, one for each variable.Systematic Error
: Systematic error refers to a consistent bias or deviation in the measurement process that affects the accuracy of data. It is not due to chance and can lead to results that are consistently higher or lower than the true value.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.