Calculating Values
There are two important values that we need to calculate in order to carry out a test for the difference in two population proportions. We need to calculate a z-score and a p-value. Both need to be included in our response to inference-related FRQs to receive full credit.

Z-Score
The z-score for our test is our critical value. We can calculate it by using the formula for any z-score:
.png&w=828&q=75)
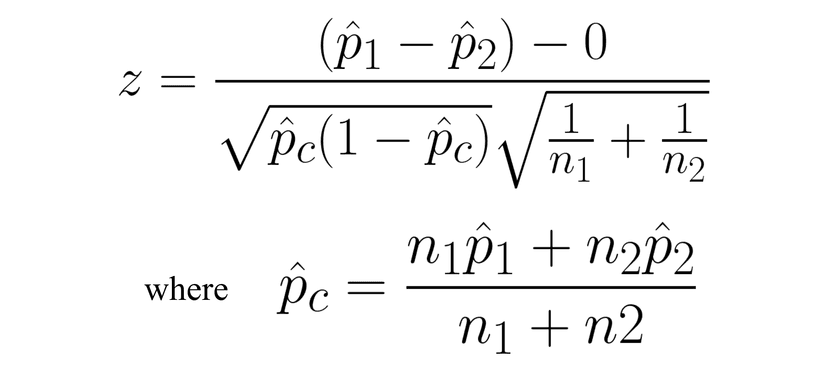
That formula looks pretty icky. Luckily if we run our test on a calculator, the z-score is part of our calculator output.
P-Value
As with any p-value, we are using the normal curve and our z-score to calculate the probability of obtaining such a value (or one less than/greater than) that value. Also, using a calculator here is much easier than doing it by hand.
Concluding the Test
Once we have our p-value and z-score, we can then make a judgment to either reject or fail to reject our null hypothesis.
Using P-Value
If you are using a p-value to perform a significance test for the difference in two population proportions, you compare the p-value to the significance level to determine whether to reject the null hypothesis. The significance level is the probability of rejecting the null hypothesis when it is actually true. It is usually set at 0.05, which means that there is a 5% chance of rejecting the null hypothesis when it is actually true.
If the p-value is less than the significance level, it means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. This gives you reason to reject the null hypothesis and conclude that there is a difference between the two population proportions. This means that it was an extremely rare occurrence (WOW value!) and we have reason to believe our null hypothesis (center of our sampling distribution) wasn't accurate.
On the other hand, if the p-value is greater than the significance level, it means that the difference is not statistically significant and may have occurred by chance. In this case, you cannot reject the null hypothesis and must conclude that there is no difference between the two population proportions.
Therefore, if the p is low, reject the H0.
Using Z-Score
If you are using a z-score to perform a significance test for the difference in two population proportions, you can use the empirical rule to determine whether the z-score represents an extremely rare value on the sampling distribution. The empirical rule states that for a normal distribution, approximately 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations.
So if the z-score is higher than 2 or 3, it is considered an extremely rare value on the sampling distribution, and you can reject the null hypothesis with a high degree of confidence. This means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. On the other hand, if the z-score is less than 2 or 3, it is not considered an extremely rare value and you cannot reject the null hypothesis. This means that the difference between the two population proportions is not statistically significant and may have occurred by chance.
Continued Example
Let's continue our example of MJ vs. Lebron to see if we can verify our conclusion from Unit 6.9. Recall that Michael Jordan made 836/1623 shots and Lebron James made 622/1493 shots. We are seeing if our data gives significant statistical evidence that Michael Jordan is actually better than Lebron.
Calculations
To avoid the lengthy and cumbersome formulas above, we are going to use a graphing calculator and the appropriate "2 Prop Z Test" to test our hypothesis:
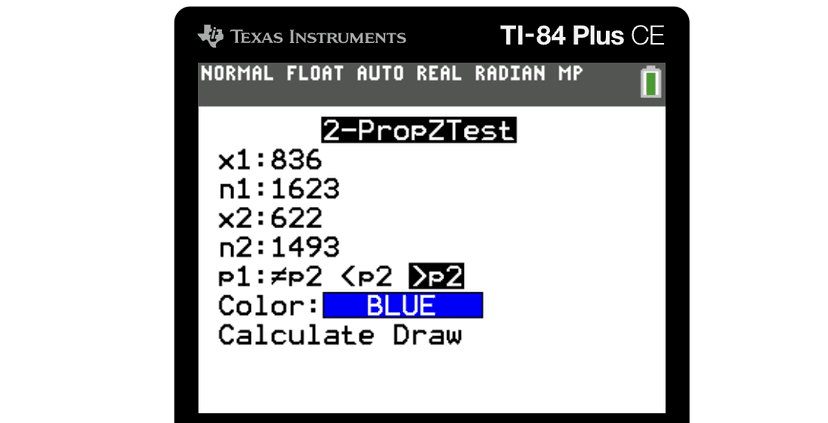
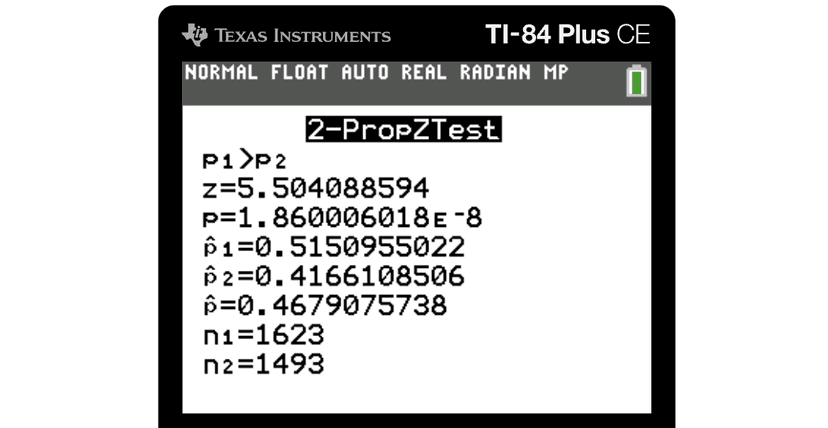
The two big values that we need to write down from our output is our z-score and p-value.
Conclusion
To conclude our test, we can look at how low our p-value is, or how high our z-score is.
P-Value
Our p-value is the best way to conclude. In this problem, we can see that our p-value is essentially 0. Therefore, we can say:
"Since our p-value is less than 0.05 (~0 < 0.05), we reject our Ho. We have convincing evidence that the true population proportion of shots made by MJ is higher than the true population proportion of shots made by Lebron."
Notice that this supports our conclusion from the confidence interval. ✔️
Z-Score
If not given the data to calculate a p-value or if only given the z-score, we can still make a judgment on the null hypothesis. In the example above, we end up with a z-score of 5.5, which is pretty extreme. Therefore, we can conclude that we can reject our null hypothesis in favor of our alternate hypothesis! ✔️
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| difference in sample proportions | The difference between two sample proportions (p̂₁ - p̂₂) used to compare proportions from two different samples. |
| difference of two population proportions | The comparison between two population proportions, expressed as p₁ - p₂, to determine if they differ significantly. |
| null hypothesis | The initial claim or assumption being tested in a hypothesis test, typically stating that there is no effect or no difference. |
| p-value | The probability of observing a test statistic as extreme as or more extreme than the one calculated from the sample data, assuming the null hypothesis is true. |
| pooled proportion | A combined estimate of the population proportion calculated from both samples when assuming the null hypothesis is true: p̂c = (n₁p̂₁ + n₂p̂₂)/(n₁ + n₂). |
| population proportion | The true proportion or percentage of a characteristic in an entire population, typically denoted as p. |
| reject the null hypothesis | The decision made when the p-value is less than or equal to the significance level, indicating sufficient evidence against the null hypothesis. |
| significance level | The threshold probability (α) used to determine whether to reject the null hypothesis in a significance test. |
| significance test | A statistical procedure used to determine whether there is sufficient evidence to reject the null hypothesis based on sample data. |
| standard error | The standard deviation of a sampling distribution, which measures the variability of a sample statistic across repeated samples. |
| test statistic | A calculated value used to determine whether to reject the null hypothesis in a hypothesis test, computed from sample data. |
Frequently Asked Questions
How do I calculate the test statistic for the difference of two proportions?
Use the two-proportion z test. Steps and formula: 1) Compute sample proportions p̂1 = x1/n1 and p̂2 = x2/n2. 2) Under H0: p1 = p2, compute the pooled proportion p̂c = (x1 + x2) / (n1 + n2). 3) Standard error (pooled) = sqrt[ p̂c(1 − p̂c) * (1/n1 + 1/n2) ]. 4) Test statistic: z = (p̂1 − p̂2) / [sqrt{p̂c(1−p̂c)(1/n1 + 1/n2)}]. Compare z to the standard normal to get a p-value (two-sided or one-sided depending on Ha). Check conditions: independent random samples and large counts (n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) all ≥ ~10). Note: AP won’t give every formula on the formula sheet but you can build it from the general test-statistic idea (statistic − parameter)/SE. For a focused review see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL), Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6), and practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the formula for z when comparing two population proportions?
Use the two-proportion z test. Under H0: p1 = p2 (so difference = 0) the test statistic is z = (p̂1 − p̂2) / [ sqrt( p̂c(1 − p̂c) * (1/n1 + 1/n2) ) ], where the pooled proportion p̂c = (n1·p̂1 + n2·p̂2) / (n1 + n2) = (X1 + X2) / (n1 + n2). Remember the conditions: two independent random samples and large counts (n1p̂c, n1(1−p̂c), n2p̂c, n2(1−p̂c) all ≥ about 10). The z value is compared to the standard normal to get a p-value (one- or two-sided depending on the alternative). The CED notes this pooled standard error and that test-statistic formulas aren’t on the AP formula sheet but can be built from general test-statistic and SE ideas. For a focused review see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL) and try practice problems at (https://library.fiveable.me/practice/ap-statistics).
When do I use a two proportion z test vs a one proportion z test?
Use a one-proportion z-test when you’re testing a claim about a single population proportion (H0: p = p0). Use a two-proportion z-test when you’re comparing two independent population proportions (H0: p1 = p2 or p1 − p2 = 0). Key differences (AP language): - One-prop z-test uses p̂ and SE = √[p0(1−p0)/n]. You assume the null value p0 when computing the SE. - Two-prop z-test (the CED’s VAR-6.K) compares p̂1 − p̂2 and—when H0 assumes equality—uses the pooled proportion p̂c = (x1 + x2)/(n1 + n2) and the pooled SE: √[p̂c(1−p̂c)(1/n1 + 1/n2)]. That pooled SE and test statistic appear in Topic 6.11. Conditions: both tests need independent random samples and large counts (np and n(1−p) checks). On the AP exam you can build these formulas from the general test-statistic form; they aren’t required to be memorized on the formula sheet (see the Topic 6.11 study guide for details: https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For extra practice, check Unit 6 (https://library.fiveable.me/ap-statistics/unit-6) and the practice problems (https://library.fiveable.me/practice/ap-statistics).
Can someone explain what p̂c means and how to calculate it step by step?
p̂c is the pooled sample proportion used in a two-proportion z-test when H0 assumes p1 = p2. It’s your best single estimate of the common population proportion under the null. Steps to get it: 1. Count successes in each sample: X1 = n1·p̂1 and X2 = n2·p̂2 (or use the raw counts if given). 2. Add successes: Xc = X1 + X2. 3. Add sample sizes: nc = n1 + n2. 4. Compute pooled proportion: p̂c = Xc / nc = (n1·p̂1 + n2·p̂2) / (n1 + n2). 5. Use p̂c in the pooled SE: SE = sqrt[ p̂c(1−p̂c) · (1/n1 + 1/n2) ]. 6. Form the z statistic: z = (p̂1 − p̂2) / SE (since H0: p1 − p2 = 0). Remember: you only pool when the null says p1 = p2. Also check large counts (n1·p̂c, n1(1−p̂c), n2·p̂c, n2(1−p̂c) all ≥ about 10) and independence before using the normal approximation. For the AP CED formula and more examples, see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For unit review and extra practice (1000+ problems), check (https://library.fiveable.me/ap-statistics/unit-6) and (https://library.fiveable.me/practice/ap-statistics).
I'm confused about the pooled proportion - why do we pool the proportions together?
You pool because the test assumes the two true population proportions are equal under the null (H₀: p₁ = p₂). If p₁ = p₂, the best single estimate of that common proportion is the combined success count divided by the combined sample size, p̂c = (x₁ + x₂)/(n₁ + n₂). Using p̂c in the standard error (√[p̂c(1−p̂c)(1/n₁ + 1/n₂)]) gives the correct variability for the sampling distribution when H₀ is true, so your z statistic tests the null properly. Don’t pool when you’re making a confidence interval—there you use the separate sample proportions for the standard error. The pooled-proportion idea and formula are in the CED (VAR-6.K.1); review the Topic 6.11 study guide for a worked example (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For more practice, see the Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6) and the practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the difference between testing if two proportions are equal vs testing if one is greater than the other?
Short answer: the null is the same (H0: p1 = p2 or p1 − p2 = 0) but the alternative changes what p-values you compute and how you decide. - Two-sided test (Ha: p1 ≠ p2): you ask whether the proportions are different in either direction. Compute the two-proportion z using the pooled proportion p̂c = (n1 p̂1 + n2 p̂2)/(n1 + n2) and z = (p̂1 − p̂2) / [√(p̂c(1 − p̂c)) √(1/n1 + 1/n2)] (VAR-6.K.1). The p-value is the probability of seeing a z as extreme or more in either tail. - One-sided test (Ha: p1 > p2 or Ha: p1 < p2): same z but the p-value is the area in one tail only (right tail for p1 > p2, left tail for p1 < p2). That makes it easier to reject H0 if the data go in the hypothesized direction but you can’t claim an effect in the other direction. Interpretation/decision: compute p-value assuming H0 true (DAT-3.C.1); if p ≤ α reject H0 (DAT-3.D.1). For review, see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL) and more unit resources (https://library.fiveable.me/ap-statistics/unit-6). For practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
How do I interpret the p-value when I'm testing the difference between two population proportions?
The p-value tells you how surprising your observed sample difference (p̂1 − p̂2) is if the null hypothesis p1 = p2 were true. Concretely: you compute the two-proportion z test (using the pooled proportion p̂c when H0: p1 = p2 is assumed), then the p-value is the probability, under that null model, of getting a sample difference as extreme or more extreme than what you saw (one-sided or two-sided depends on your Ha). Interpretation in context: a small p-value (≤ α) means the observed difference is unlikely under H0, so reject H0 and conclude there’s convincing statistical evidence of a difference in the population proportions. A large p-value (> α) means the data are consistent with H0, so fail to reject H0 (don’t say “accept”). Remember AP advice: the p-value is computed assuming the null is true (CED DAT-3.C.1), compare p to α for your decision (CED DAT-3.D.1), and use the pooled SE for the z formula (CED VAR-6.K.1). For a focused review, check the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For more practice, try the AP Stats problems at Fiveable (https://library.fiveable.me/practice/ap-statistics).
I don't understand why we assume the null hypothesis is true when calculating the p-value - can someone explain this?
When you compute a p-value you’re asking one question: “If the null hypothesis were true, how likely is an outcome at least as extreme as what we observed?” So we assume H0 is true to get the sampling distribution of the statistic. For a two-proportion z-test, H0: p1 = p2 means the center of the sampling distribution of p̂1 − p̂2 is 0, and we use the pooled proportion p̂c = (x1 + x2)/(n1 + n2) to estimate the common p when calculating the pooled standard error (see VAR-6.K.1). The p-value is then the probability, under that null distribution (standard normal for the z), of seeing a difference as big (or bigger) than the observed p̂1 − p̂2. Finally, compare that p-value to α to decide: p ≤ α → reject H0; p > α → fail to reject H0 (DAT-3.D.1). Want extra practice? Check the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL) and more problems at (https://library.fiveable.me/practice/ap-statistics).
What are the conditions I need to check before doing a two proportion z test?
Before you do a two-proportion z test check three things: 1. Randomness/independence—each sample must be from a random sample or randomized experiment and the two samples must be independent (no matched/paired data). If sampling without replacement, each sample should be ≤10% of its population. 2. Large counts (normal approximation)—under H0 (p1 = p2) use the pooled proportion p̂c = (x1 + x2)/(n1 + n2). Then check that n1·p̂c, n1·(1−p̂c), n2·p̂c, and n2·(1−p̂c) are all at least about 10 so the sampling distribution of p̂1−p̂2 is approximately normal. 3. Context & hypotheses—state H0: p1 = p2 (or p1−p2 = 0) and the correct one- or two-sided Ha. If conditions fail, use a simulation or exact method instead. The test statistic you’ll use is z = (p̂1 − p̂2)/√[p̂c(1−p̂c)(1/n1 + 1/n2)] (you can build it from the AP formula sheet). For a short study guide, see the Topic 6.11 page (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For more practice, try the AP problems (https://library.fiveable.me/practice/ap-statistics).
How do I know if I should reject or fail to reject the null hypothesis in a two proportion test?
Do the test math (or get your calculator to) and then compare the p-value to your α. 1. Compute p̂1, p̂2 and the pooled proportion p̂c = (n1p̂1 + n2p̂2)/(n1 + n2). 2. Find the z statistic: z = (p̂1 − p̂2) / [√(p̂c(1−p̂c)) √(1/n1 + 1/n2)]. (This is the CED formula for VAR-6.K.1.) 3. Get the p-value from the standard normal using that z. For a two-sided alternative (Hₐ: p₁ ≠ p₂) double the one-tail area; for one-sided, use the appropriate tail. 4. Decision rule (DAT-3.D.1): if p-value ≤ α, reject H₀: p₁ = p₂. If p-value > α, fail to reject H₀. Always state your conclusion in context (e.g., “reject—evidence that the proportions differ”). 5. Check conditions (independent random samples, large counts np and n(1−p) for each sample) before trusting the z-test. Want step-by-step practice? See the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL) and more practice problems (https://library.fiveable.me/practice/ap-statistics).
My calculator keeps giving me different answers for the pooled proportion - what am I doing wrong?
If your calculator keeps giving different pooled proportions, you’re probably entering the wrong inputs or rounding too early. For the two-proportion z-test the pooled proportion is p̂c = (x1 + x2) / (n1 + n2), which is algebraically the same as (n1·p̂1 + n2·p̂2)/(n1 + n2). Common mistakes: - Entering p̂1 and p̂2 into a calculator command that expects counts (x1, x2)—different calculators use different input orders (counts vs. proportions). - Rounding p̂1 or p̂2 before combining them. Always compute x1 = n1·p̂1 and x2 = n2·p̂2 (use whole counts) then form p̂c. - Swapping n1/n2 or using the pooled formula only for the SE but not for z numerator (inconsistent use). Remember the AP CED formula and that the exam won’t give this formula on the sheet, so be ready to build it from counts (see Topic 6.11 study guide: https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For practice, try problems at the unit page (https://library.fiveable.me/ap-statistics/unit-6) or the practice bank (https://library.fiveable.me/practice/ap-statistics).
When the problem says "is there a significant difference between the two groups," what hypotheses should I write?
Write the null as “no difference” and the alternative as “there is a difference.” In symbols (two-sided test): H₀: p₁ = p₂ (equivalently p₁ − p₂ = 0) Hₐ: p₁ ≠ p₂ (equivalently p₁ − p₂ ≠ 0) Use the pooled proportion p̂c = (x₁ + x₂)/(n₁ + n₂) when computing the two-proportion z statistic (see VAR-6.K.1). After you compute z and the p-value, compare the p-value to your α: if p-value ≤ α reject H₀ (evidence of a difference); if p-value > α fail to reject H₀ (no convincing evidence). The AP exam expects you to state hypotheses in context (mention the two groups) and justify conclusions by comparing p-value to α. For a refresher on the procedure see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL)—and practice more problems at (https://library.fiveable.me/practice/ap-statistics).
I missed class and I'm lost - what's the step by step process for a two proportion significance test?
Here’s a short step-by-step for a two-proportion z-test (AP Topic 6.11): 1. State hypotheses in context. Common null: H0: p1 = p2 (or p1 − p2 = 0). Choose Ha: p1 ≠ p2, p1 > p2, or p1 < p2. 2. Check conditions: independent random samples, and large counts for pooled check: n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) all ≥ about 10 (use p̂c below). 3. Compute pooled proportion p̂c = (x1 + x2)/(n1 + n2). 4. Compute SE under H0: SE = sqrt[p̂c(1−p̂c) * (1/n1 + 1/n2)]. 5. Compute test statistic: z = (p̂1 − p̂2 − 0) / SE. (CED formula.) 6. Find p-value from standard normal (two-sided or one-sided as per Ha). 7. Decision: if p-value ≤ α reject H0; if > α fail to reject. 8. Interpret in context, and explain p-value as probability of data (or more extreme) assuming H0 true. For AP-style review, see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For more Unit 6 review and practice, check the unit page (https://library.fiveable.me/ap-statistics/unit-6) and lots of practice problems (https://library.fiveable.me/practice/ap-statistics).
Why do we use the pooled proportion in the denominator instead of separate standard errors for each group?
We use the pooled proportion because the test assumes the null hypothesis p1 = p2. Under H0 the two samples come from the same population proportion, so the best single estimate of that common p is the combined (pooled) proportion p̂c = (x1 + x2)/(n1 + n2). Plugging p̂c into the standard error gives the correct variability of p̂1 − p̂2 under the null: √[p̂c(1−p̂c)(1/n1 + 1/n2)]. If you used the separate sample SEs (which use p̂1 and p̂2) you'd be estimating variability as if the proportions could differ—that’s appropriate for a confidence interval, but not for a significance test that computes probabilities assuming p1 = p2. This distinction (pooled SE for tests, separate SE for CIs) is exactly what the CED formula and Topic 6.11 emphasize. For a quick refresher, see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL). For more practice, check the Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6) and AP practice problems (https://library.fiveable.me/practice/ap-statistics).
How do I write a conclusion for a two proportion test that actually answers the research question?
Write your conclusion in three short pieces so it answers the research question directly. 1) State the decision: compare p-value to α. Example: “p = 0.03 < 0.05, so reject H₀: p₁ = p₂.” 2) Answer the research question in context (the claim): “There is convincing statistical evidence that the proportion of [population 1 doing X] is higher than the proportion of [population 2 doing X].” (If p > α, say “fail to reject H₀” and “the data do not provide convincing evidence of a difference.”) 3) Brief justification linking method to result: “We used a two-proportion z-test (pooled proportion p̂c for the SE). The p-value was computed assuming H₀ is true, and comparing it to α gives the decision above.” Short template you can copy: - Decision: “Reject/Fail to reject H₀ (p = ___, α = ___).” - Answer: “Therefore, there is / is not convincing evidence that [state difference in plain context].” - Why: “Because the p-value is [< or >] α; test used: two-proportion z-test (pooled SE).” For step-by-step examples and practice, see the Topic 6.11 study guide (https://library.fiveable.me/ap-statistics/unit-6/carrying-out-test-for-difference-two-population-proportions/study-guide/mkdLDKdZAuQ6pIsV3aOL) and try more problems at (https://library.fiveable.me/practice/ap-statistics).