Calculating T-Scores
The first step in actually performing any statistical significance test is to calculate the test statistic used for that particular test. Since we are carrying out a significance test for a population mean, we should calculate a t-score.
The t-score is a test statistic that is used in a t-test to evaluate the significance of the difference between the sample mean and a hypothesized population mean.
The t-score is calculated by dividing the difference between the sample mean and the hypothesized mean by the standard error of the mean. (The standard error of the mean is a measure of the variability of the sample mean and is calculated by dividing the standard deviation of the sample by the square root of the sample size.)
The larger the t-score, the more significant the difference between the sample mean and the hypothesized mean is.
When calculating a t-score, we use the general formula for critical values:
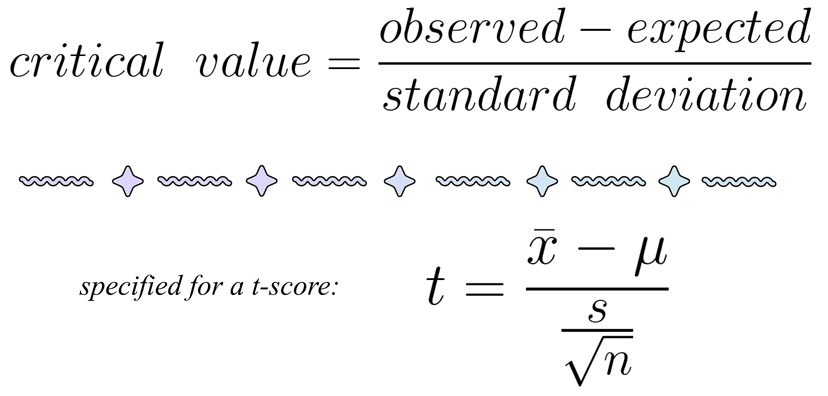
Where x̄ is our sample mean, 𝞵 is our hypothesized sample mean, s is our standard deviation of our sample and n is our sample size.

Example
Ricardo has a bag of 30 oranges. The bag says that each orange weighs an average of 4.5 oz.
Ricardo weighs all of the oranges in his bag and finds that they have an average of 4.65 oz with a standard deviation of 0.8 oz.
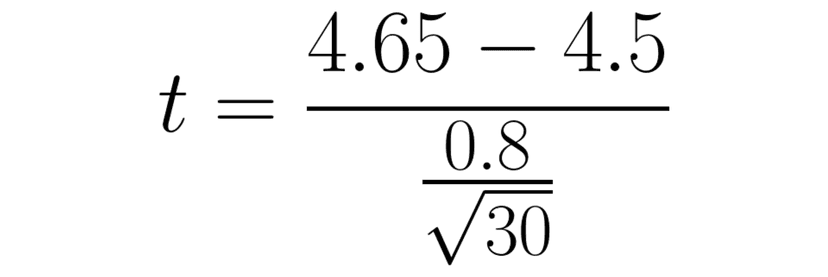
Calculating P-Value
When performing a hypothesis test, we could be performing either a one-tailed or two-tailed test. This depends on our alternate hypothesis when setting up our test.
The type of hypothesis test (one-tailed or two-tailed) is determined by the alternative hypothesis that you specify. If the alternative hypothesis is directional (e.g. "the population mean is greater than X"), then you would perform a one-tailed test because you're looking for a t-score only in one tail of our curve.
On the other hand, if the alternative hypothesis is non-directional (e.g. "the population mean is not equal to X"), then you would perform a two-tailed test since we are looking to find a t-score in either tail of our curve.
It's important to note that the choice of one-tailed or two-tailed test can have a significant impact on the results of the hypothesis test. A one-tailed test is more powerful than a two-tailed test because it allows you to detect a difference in a specific direction (e.g. the population mean is greater than X). However, this increased power comes at the cost of increased risk of a type I error (rejecting the null hypothesis when it is true). A two-tailed test is less powerful than a one-tailed test, but it reduces the risk of a type I error because it is not biased towards any particular direction.
Back to the hypothesis test, we'll then need to reference our t-score chart to calculate our p value.
First, let's determine the degrees of freedom, which is always one less than our sample size.
Then, we find our t-score in the column matching our given degrees of freedom (df) to estimate our p-value. If the degrees of freedom can not be found in the chart, round down to the nearest df.
Example
In our example above with Ricardo's oranges, our df = 29. So we need to locate 29 df on the chart and then try to find 1.027.
We can see in the t table, that the tail probability with df=29 and t-score of 1.027 is approximately 0.15 (since its close to 1.055).
- If we are doing a one tailed test, this is our p-value.
- If we are doing a two tailed test, we would double this to get 0.3 for our p-value (since the t curve is symmetric and tail probabilities are equal).
Using Calculator to Calculate T-Score and P-Value
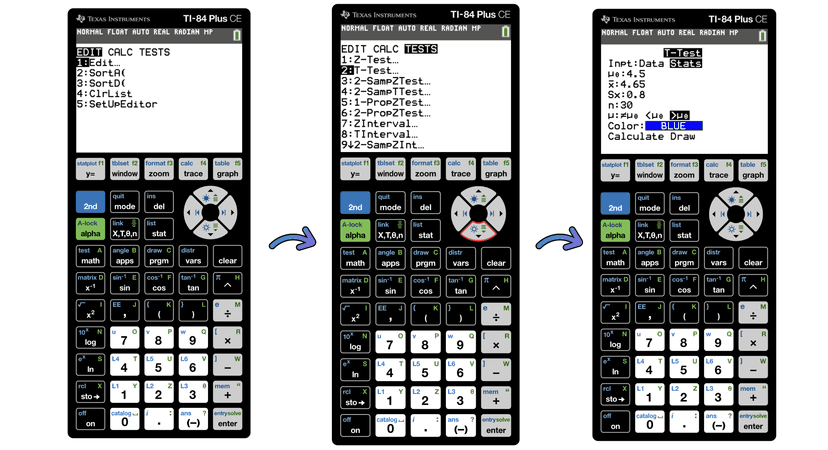
Perhaps a much easier way to perform a one sample t test would be to use technology such as a graphing calculator. The most commonly used calculator for AP Statistics is the Texas Instruments TI-84.
When performing a one sample t test, you will first enter into the stats menu.
Then, you will navigate over to tests and select option 2.
You are then given two options: you can enter the given sample statistics or let the calculator use data points entered in Lists to calculate your necessary test statistic and p value. We will proceed with our example using Ricardo's oranges.
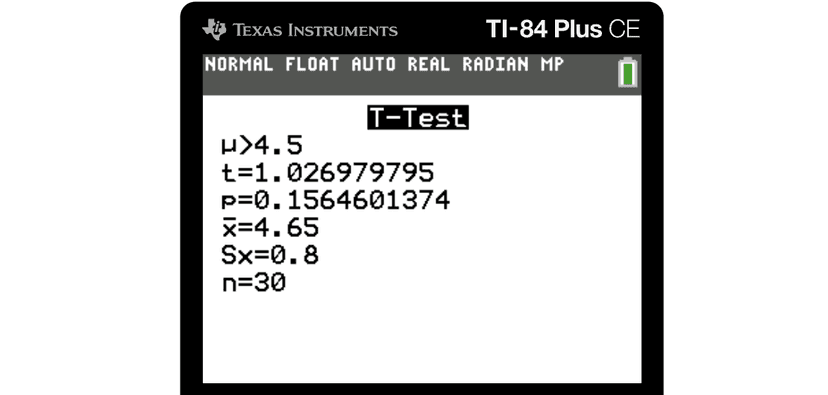
Once you press calculate, it gives you your test statistic and p value. Both of these things are essential to list out in your written response to receive full credit on the AP exam. Also, it is important for a t-test for population mean to include your degrees of freedom, even though it is not listed in the computer output for the test.
Using P-Value to Make Conclusions
Once you have calculated the test statistic and p-value for your hypothesis test, you can use them to draw conclusions about the data. After all, the p-value is a measure of the likelihood of obtaining the observed results (or more extreme results) under the assumption that the null hypothesis is true.
If the p-value is less than the predetermined level of significance (usually 0.05), it means that the observed results are unlikely to have occurred by chance alone, and you can reject the null hypothesis in favor of the alternative hypothesis. On the other hand, if the p-value is greater than the level of significance, it means that the observed results are not statistically significant and you cannot reject the null hypothesis.
Templates
- p < 𝞪: "Since p < 𝞪, we reject our Ho. We have convincing evidence at the 𝞪 level that (Ha in context of problem)."
- p > 𝞪: "Since p > 𝞪, we fail reject our Ho. We do not have convincing evidence at the 𝞪 level that (Ha in context of problem)."
As always, we NEVER "accept" a null or alternate hypothesis.
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Means
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| degrees of freedom | A parameter of the t-distribution that affects its shape; as degrees of freedom increase, the t-distribution approaches the normal distribution. |
| matched pairs | Paired observations where two measurements are taken on the same subject or on subjects that are matched according to specific criteria, used to analyze the mean difference between the paired values. |
| null hypothesis | The initial claim or assumption being tested in a hypothesis test, typically stating that there is no effect or no difference. |
| p-value | The probability of observing a test statistic as extreme as or more extreme than the one calculated from the sample data, assuming the null hypothesis is true. |
| population mean | The average of all values in an entire population, denoted as μ. |
| population means | The average values of two distinct populations being compared, denoted as μ₁ and μ₂. |
| reject the null hypothesis | The decision made when the p-value is less than or equal to the significance level, indicating sufficient evidence against the null hypothesis. |
| sample mean | The average of all values in a sample, denoted as x̄, used as an estimate of the population mean. |
| sampling distribution | The probability distribution of a sample statistic (such as a sample proportion) obtained from repeated sampling of a population. |
| significance level | The threshold probability (α) used to determine whether to reject the null hypothesis in a significance test. |
| significance test | A statistical procedure used to determine whether there is sufficient evidence to reject the null hypothesis based on sample data. |
| standard error | The standard deviation of a sampling distribution, which measures the variability of a sample statistic across repeated samples. |
| t-distribution | A probability distribution used when the population standard deviation is unknown and the sample standard deviation is used instead, characterized by heavier tails than the normal distribution. |
| test statistic | A calculated value used to determine whether to reject the null hypothesis in a hypothesis test, computed from sample data. |
Frequently Asked Questions
How do I calculate the test statistic for a population mean when I don't know the population standard deviation?
If σ is unknown, use the one-sample t statistic: t = (x̄ − μ0) / (s/√n), where x̄ is your sample mean, μ0 is the null value, s is the sample standard deviation, and n is the sample size. This t statistic follows a Student’s t distribution with df = n − 1. For matched pairs, compute differences first and then use the same formula on the differences (df = number of pairs − 1). Check the normality condition: either the population is approximately normal or n is large enough for the CLT; small skew or outliers can invalidate the t-test. Find the p-value from the t distribution (two-tailed or one-tailed depending on Ha) and compare it to α to decide (reject H0 if p ≤ α). Reminder: the AP formula sheet doesn’t list these test formulas explicitly, but you can construct them from the general test-statistic form and standard error (see the CED). Practice this on the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and more problems (https://library.fiveable.me/practice/ap-statistics).
What's the formula for the t-test statistic and how is it different from the z-test?
t-test statistic (one-sample): t = (x̄ − μ0) / (s / √n). For matched pairs, use differences d: t = (d̄ − μ0) / (sd / √n), with df = n − 1. How it’s different from a z-test: - z uses the population sd σ: z = (x̄ − μ0) / (σ / √n). Use z only when σ is known (rare in practice) or when sample size is large and you justify using σ̂ in place of σ. - t uses the sample sd s, so the test statistic follows Student’s t-distribution (wider tails) with df = n − 1; the t distribution depends on df and approaches the normal as n grows. - AP note: the exam’s formula sheet gives standard errors you can use to build these statistics, and you don’t have to memorise them (see CED VAR-7.E and the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA)). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
When do I use a t-test vs a z-test for testing population means?
Use a t-test whenever the population standard deviation σ is unknown and you estimate variability with the sample standard deviation s—that’s the usual AP case. The test statistic is t = (x̄ − μ0) / (s/√n) and follows a Student’s t-distribution with df = n − 1 (CED VAR-7.E.1). Use a z-test only when σ is known (rare in practice) so the standardized statistic uses σ and the normal (z) distribution. Notes that matter for AP: - If n is small, you need the population (or differences for matched pairs) to be approximately normal. For larger n (often n ≥ 30) the CLT helps, but if σ is unknown you still use the t-test. - For matched-pairs inference, compute differences and do a one-sample t-test on those differences (paired t). - Compare p-value to α to make decisions (DAT-3.F). Review the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and practice lots of problems (https://library.fiveable.me/practice/ap-statistics).
Can someone explain step by step how to do a significance test for a population mean?
Quick step-by-step for a one-sample (or paired) t test for a population mean: 1. State hypotheses. Null: H0: μ = μ0. Alternative: Ha: μ ≠ μ0 (two-tailed) or μ > μ0 / μ < μ0 (one-tailed). For matched pairs, do the test on the differences d and use μd. 2. Check conditions: data are random, population (or differences) ~ normal OR n ≥ 30 (CLT). 3. Compute statistic: t = (x̄ − μ0) / (s/√n). For paired, x̄ is mean difference and s is sd of differences. Degrees of freedom = n − 1. (You won’t be given the formula sheet t formula on the exam, but you can build it from “statistic − parameter over SE” as the CED says.) 4. Find p-value using t(df = n−1): two-tailed = 2·P(T ≥ |t|). Use a calculator or Table B. 5. Make decision: if p ≤ α reject H0; if p > α fail to reject H0. 6. Interpret in context: state what your decision says about the population mean, and remember p-value assumes H0 true. For practice and worked examples, see the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA), the Unit 7 overview (https://library.fiveable.me/ap-statistics/unit-7), and 1000+ practice problems (https://library.fiveable.me/practice/ap-statistics).
What does degrees of freedom mean and how do I calculate n-1 for a t-test?
Degrees of freedom (df) is basically how many independent pieces of information you have left to estimate variability after using one piece to estimate the mean. For a one-sample or paired t-test, you estimate the population mean with x̄, which "uses up" 1 piece of info, so df = n − 1. That df is what the CED calls out: the t statistic t = (x̄ − μ)/(s/√n) follows a t-distribution with n − 1 degrees of freedom (VAR-7.E.1). How to compute it: if your sample size is n = 12, then df = 12 − 1 = 11. For a matched-pairs test, n is the number of pairs (so 20 pairs → df = 19). On the AP exam you won’t be given t formulas on the formula sheet, but you can construct the test statistic from the general form and use the t table with df = n − 1 (see Topic 7.5 study guide for examples: https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
I'm confused about interpreting p-values - what does it actually mean when p = 0.03?
A p-value of 0.03 means: assuming the null hypothesis is true (that the population mean equals μ0), there's a 3% chance you'd get a sample result as extreme as—or more extreme than—the one you observed. It's a probability about the data under H0, not the probability that H0 is true. How you act on it: compare p to your significance level α. If α = 0.05, p = 0.03 ≤ α, so you reject H0 and say the data provide convincing statistical evidence for the alternative (DAT-3.F). If α = 0.01, you’d fail to reject H0. Quick reminders for AP Stats: p-values are computed assuming H0 is true (DAT-3.E.1) and your formal decision explicitly compares p to α (DAT-3.F.1). For more on one-sample/paired t-tests and practice, check the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and the Unit 7 overview (https://library.fiveable.me/ap-statistics/unit-7). For extra practice (1000+ problems) see (https://library.fiveable.me/practice/ap-statistics).
How do I know whether to reject or fail to reject the null hypothesis?
Compute the test statistic (for a mean use t = (x̄ − μ0) / (s/√n) with df = n − 1) and find the p-value assuming H0 is true. Then compare that p-value to your chosen significance level α. - If p-value ≤ α → reject H0 (there’s convincing statistical evidence for Ha). - If p-value > α → fail to reject H0 (not enough evidence to support Ha). Also keep these AP-specific points in mind (CED keywords): use the t-distribution for means when σ is unknown, choose a one- or two-tailed p-value to match your alternative hypothesis, and state your conclusion in context (mention the population and parameter). The AP formula sheet won’t list that t formula explicitly, but you can build it from the general test-statistic form (see the Topic 7.5 study guide on Fiveable: https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA). For extra practice, try problems at https://library.fiveable.me/practice/ap-statistics.
What's the difference between testing a single mean and testing matched pairs?
Testing a single mean (one-sample t-test) vs. matched pairs (paired t-test) is mostly about what your “data point” is. - One-sample t-test: each observation is an independent measurement from the population. Test statistic t = (x̄ − μ0)/(s/√n) with df = n − 1. Use when you sample one group and compare its mean to a hypothesized μ (CED VAR-7.E). - Matched pairs: you have paired or repeated measurements (before/after, matched subjects). You first compute each pair’s difference d = x1 − x2, then do a one-sample t-test on the differences: t = (d̄ − 0)/(sd/√n) with df = n − 1. So conceptually it’s a one-sample test on differences, not a two-sample test. Key assumption: the distribution of the pairwise differences is approximately normal (or n large/Central Limit Theorem applies). In both tests you interpret the p-value by assuming H0 true and compare p to α to reject or fail to reject (CED DAT-3.E, DAT-3.F). For quick review, see the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA), the Unit 7 overview (https://library.fiveable.me/ap-statistics/unit-7), and practice problems (https://library.fiveable.me/practice/ap-statistics).
Why do we assume the null hypothesis is true when calculating the p-value?
We assume the null hypothesis is true because the p-value is defined as the probability of seeing data at least as extreme as ours under that specific baseline model. In a one-sample t-test you compute t = (x̄ − μ0) / (s/√n) and then use the t distribution (df = n−1) to find how likely a t that extreme would be if μ = μ0 (VAR-7.E.1 and DAT-3.E.1). Treating H0 as true gives a clear, common reference model so you can calculate tail probabilities and compare the p-value to α to make a decision (DAT-3.F.1). If the p-value ≤ α, the observed result is rare under H0, so you reject H0; if p > α, the data aren’t surprising enough, so you fail to reject. Want more practice interpreting p-values and t tests? Check the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and thousands of practice problems (https://library.fiveable.me/practice/ap-statistics).
How do I set up the null and alternative hypotheses for a population mean test?
Start by identifying the parameter: μ, the population mean. The null hypothesis (H0) always states a specific value for μ (the “no effect” or status-quo): H0: μ = μ0. The alternative (Ha) expresses the research question and dictates the test type: - Two-tailed (difference?): Ha: μ ≠ μ0—use when you want to detect any change. - Right-tailed (greater?): Ha: μ > μ0—use when you’re testing for an increase. - Left-tailed (less?): Ha: μ < μ0—use when you’re testing for a decrease. For matched pairs, work with differences d and test H0: μd = 0 (or μd = d0) with Ha written the same way but for μd. Remember the AP requirements: you'll use the t statistic t = (x̄ − μ0)/(s/√n) and t has df = n−1 (CED VAR-7.E). Compute the p-value assuming H0 is true (CED DAT-3.E) and compare to α: reject H0 if p ≤ α, fail to reject if p > α (CED DAT-3.F). For a quick review, see the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and more practice problems (https://library.fiveable.me/practice/ap-statistics).
What conditions do I need to check before doing a t-test for a population mean?
Before you run a one-sample or paired t-test for a mean check three things: 1. Randomness/independence—data come from a random sample or randomized experiment, and if sampling without replacement the sample is ≤10% of the population. 2. Normality of the sampling distribution—either the population is approximately normal or the sample is large enough for the CLT to kick in (a common rule: n ≥ 30). For small samples (n < 30) you need the original data (or paired differences) to be roughly symmetric and free of strong skew or outliers. For matched-pairs, check these conditions on the difference scores. 3. Use the correct t model—if conditions hold, the test statistic t = (x̄ − μ0)/(s/√n) follows a t distribution with df = n − 1 (or df = number of pairs − 1 for paired tests), and compare the p-value to α to decide (DAT-3.F). For a quick refresher and examples, see the Fiveable Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
I don't understand when to use one-tailed vs two-tailed tests for population means
Use a one- or two-tailed test based on the research question—that decides your alternative hypothesis (Ha): - Two-tailed (Ha: μ ≠ μ0): use when you’re testing for any difference from μ0 (e.g., “Is the mean different from 50?”). This splits the rejection region into both tails. - One-tailed (Ha: μ > μ0 or Ha: μ < μ0): use when you have a directional claim (e.g., “Is the mean greater than 50?” → Ha: μ > 50). Put all the rejection area in that one tail. In AP terms, set H0: μ = μ0 and choose Ha to match the context. Compute the t statistic t = (x̄ − μ0)/(s/√n) (one-sample or paired t for matched differences) and compare the p-value to α: if p ≤ α reject H0 (CED DAT-3.F). Remember the test type must come from the question’s claim before you look at data. For more practice and examples see the Unit 7 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) or the unit overview (https://library.fiveable.me/ap-statistics/unit-7) and try problems (https://library.fiveable.me/practice/ap-statistics).
How do I find the p-value on my calculator after getting the t-statistic?
After you compute t = (x̄ − μ0) / (s/√n) and know df = n − 1, use your graphing calculator’s Student t CDF to get the p-value. On a TI-83/84 the command is tcdf(lower, upper, df). - Left-tailed Ha: μ < μ0—p = tcdf(−1E99, t, df) - Right-tailed Ha: μ > μ0—p = tcdf(t, 1E99, df) - Two-tailed Ha: μ ≠ μ0—p = 2 × tcdf(−1E99, −|t|, df) (equivalently 2 × tcdf(|t|, 1E99, df) if t>0) Quick example: t = −2.10, n = 15 → df = 14. Left-tail p = tcdf(−1E99, −2.10, 14) ≈ 0.027. Two-tailed p ≈ 2×0.027 = 0.054. Tip: many calculators also have a “T-Test” inference routine that outputs the test statistic and p-value directly (useful on the AP exam since a graphing calculator is allowed). For more review on carrying out a t-test and practice, see the Topic 7.5 study guide (https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA) and extra practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the difference between statistical significance and practical significance in hypothesis testing?
Statistical significance means your test result (like a t statistic and its p-value) is unlikely under H0. If p ≤ α you reject H0—that’s what the CED calls a formal decision (DAT-3.F). Practical (or clinical) significance asks whether the detected difference actually matters in the real world—is the size of the effect big enough to matter for decisions? Why they can differ: with large n even tiny differences give small p-values; with small n a meaningful difference might not be statistically significant. Use effect size (difference in means, Cohen’s d) and confidence intervals to judge practical importance, and always state results in context (units, who was sampled). For AP practice, make the formal p-value vs α decision, then comment on practical significance separately (CED: interpret p-value DAT-3.E and justify claim DAT-3.F). More on carrying out a mean test: https://library.fiveable.me/ap-statistics/unit-7/carrying-out-test-for-population-mean/study-guide/MDb6OWdPx2ITRYtOuvxA. For extra practice, see https://library.fiveable.me/practice/ap-statistics.
