Another way to check a statistical claim is to perform a significance test for the difference in two population proportions. As with any significance test, we have to write hypotheses, check our conditions and then calculate and conclude.
Still lost? Let's do a refresher!
A statistical significance test is used to determine whether the difference between two population proportions is statistically significant, or whether it could have occurred by chance.
To perform a significance test for the difference in two population proportions, you need to first write your null and alternative hypotheses. The null hypothesis states that there is no difference between the two population proportions, while the alternative hypothesis states that there is a difference.
Next, you need to check that the conditions for the test are met. These include having a large enough sample size and having a random and independent sample.
Once you have checked the conditions, you can calculate the test statistic and determine the p-value. The p-value is the probability of obtaining a test statistic as extreme as the one observed, given that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), you can reject the null hypothesis and conclude that the difference between the two population proportions is statistically significant. If the p-value is greater than the significance level, you cannot reject the null hypothesis and must conclude that the difference is not statistically significant.
Hypotheses and Parameters
The first thing we need to do when setting up a significance test for the difference in two population proportions is to write out our hypotheses. Our null hypotheses will always have our two population proportions being equal, while our alternate has them either greater than, less than or not equal to each other.
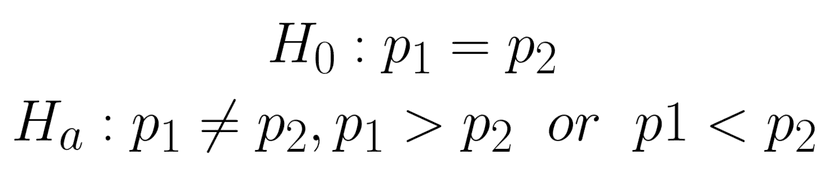
It is also important in this stage of setting up the test to identify what p1 and p2 represent. We have to define our parameters so the reader knows what we are truly comparing.

Conditions
We also must check our conditions for inference. The same three conditions apply as did for confidence intervals with one little small change in the normal check.
(1) Random
Probably the most important condition is that we need to be sure that both of our samples come from random samples. If we don't take a random sample from our population, then our findings suffer from sampling bias and we are stuck and we can't generalize our findings to our population.
(2) Independence
To check that our sample is independent, we need to make sure that both of our populations are at least 10 times that of our samples. Also, if we are dealing with a randomized experiment, the random assignment of treatments classifies our samples as independently selected.
(3) Normal
When dealing with proportions, we always check our normal condition by using the Large Counts Condition, which states that our expected successes and failures is at least 10. With a 2 proportion z test, we have to combine our proportions to create a combined p-hat. This is what we use to find our expected failures and successes.
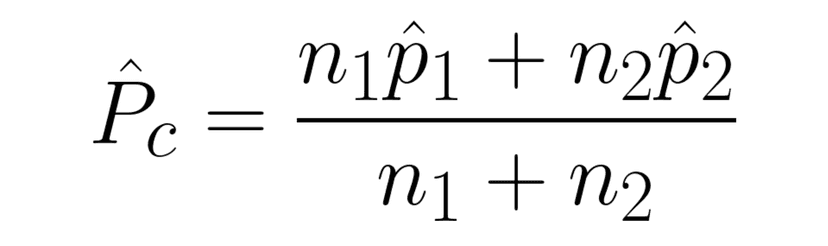
Then we have to verify that each of our expected failures and successes are at least 10.
.png&w=828&q=75)
This is because we are using a pooled sample. In this test, you combine the two samples into a single "pooled" sample and calculate a single proportion for the combined sample. The test statistic is then calculated based on the difference between the two proportions and the pooled sample proportion.
Example
Let's return to our MJ vs. Lebron problem from earlier... again. Recall that MJ made 836/1623 shots and Lebron made 622/1493 shots. Instead of testing this claim with a confidence interval, let's test it using a 2 Prop Z Test to verify our results.
Hypotheses and Parameters
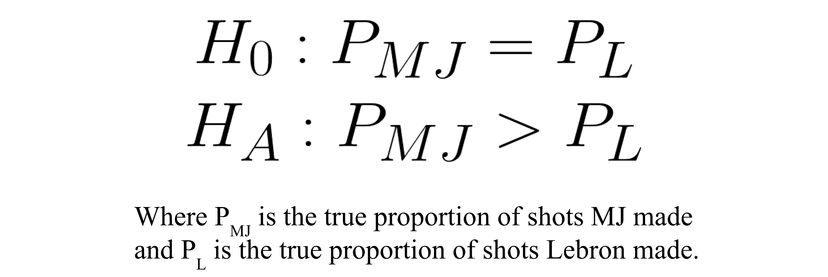
Another great idea when writing our hypotheses is to use meaningful subscripts such as MJ and L that clarify which proportion matches which population.
Conditions
- Random: Even though the problem never stated that they were random (and we discussed the problems with this in Unit 6.9) we are going to assume it is random.
- Independent: It is reasonable to believe (and obviously true) that MJ took at least 16, 230 shots in his career and Lebron took at least 14,930 shots in his career, so the samples are independent.
- Normal: This is the one that will be a bit different. First, we have to calculate our pooled p-hat. Using the formula above, we get 0.468
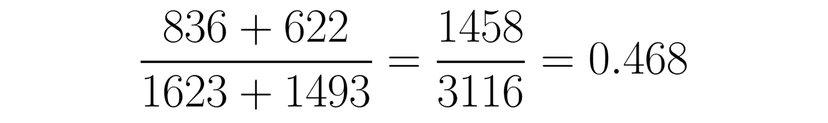
Next, we have to check our large counts condition using this pooled p-hat.
- 1623 (0.468) > 10 ✔️
- 1623 (0.532) > 10 ✔️
- 1493 (0.468) > 10 ✔️
- 1493 (0.532) > 10 ✔️
Now that we have checked conditions, we are ready to calculate and test our claim.
🎥 Watch: AP Stats - Inference: Hypothesis tests for Proportions
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| alternative hypothesis | The claim that contradicts the null hypothesis, representing what the researcher is trying to find evidence for. |
| approximately normal | A distribution that closely follows the shape of a normal distribution, allowing for the use of normal probability methods. |
| categorical variable | A variable that takes on values that are category names or group labels rather than numerical values. |
| difference of two population proportions | The comparison between two population proportions, expressed as p₁ - p₂, to determine if they differ significantly. |
| independence | The condition that observations in a sample are not influenced by each other, typically ensured through random sampling or randomized experiments. |
| null hypothesis | The initial claim or assumption being tested in a hypothesis test, typically stating that there is no effect or no difference. |
| one-sided alternative hypothesis | An alternative hypothesis that specifies the direction of the difference, either p₁ < p₂ or p₁ > p₂. |
| pooled proportion | A combined estimate of the population proportion calculated from both samples when assuming the null hypothesis is true: p̂c = (n₁p̂₁ + n₂p̂₂)/(n₁ + n₂). |
| population proportion | The true proportion or percentage of a characteristic in an entire population, typically denoted as p. |
| randomized experiment | A study design where subjects are randomly assigned to treatment groups to establish cause-and-effect relationships. |
| sampling distribution | The probability distribution of a sample statistic (such as a sample proportion) obtained from repeated sampling of a population. |
| sampling without replacement | A sampling method in which an item selected from a population cannot be selected again in subsequent draws. |
| simple random sample | A sample selected from a population such that every possible sample of the same size has an equal chance of being chosen. |
| statistical inference | The process of drawing conclusions about a population based on data collected from a sample. |
| two-sample z-test | A hypothesis test used to compare the difference between two population proportions using the standard normal distribution. |
| two-sided alternative hypothesis | An alternative hypothesis that specifies the difference could be in either direction, stated as p₁ ≠ p₂. |
Frequently Asked Questions
How do I set up null and alternative hypotheses for comparing two proportions?
For a two-sample test of proportions you always start with the null that the populations are the same (difference = 0): H0: p1 = p2 or H0: p1 − p2 = 0. The alternative depends on your question: - Two-sided: Ha: p1 ≠ p2 (tests for any difference). - One-sided: Ha: p1 > p2 or Ha: p1 < p2 (tests a directional claim). On the AP exam you’ll use a two-sample z-test for proportions (when conditions are met). Under H0 you form the pooled proportion p̂c = (x1 + x2)/(n1 + n2) and use the pooled SE: sqrt[p̂c(1−p̂c)(1/n1 + 1/n2)] to compute the z statistic. Before testing check independence (random/independent samples, 10% rule if without replacement) and the success–failure condition using the pooled p̂c: n1p̂c, n1(1−p̂c), n2p̂c, n2(1−p̂c) ≥ 5 (or 10 per your class). For a short walkthrough and examples see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP). For extra practice, try problems on the Unit 6 page (https://library.fiveable.me/ap-statistics/unit-6) or the general practice bank (https://library.fiveable.me/practice/ap-statistics).
What's the difference between a one-sample z-test and a two-sample z-test for proportions?
One-sample z-test for a proportion tests one population proportion against a hypothesized value: H0: p = p0. The test statistic is (p̂ − p0) / sqrt[p0(1−p0)/n] and you check independence (random sample, 10% condition) and success–failure using p0 (or p̂ for CI). Two-sample z-test compares two independent proportions: H0: p1 = p2 (or p1 − p2 = 0) and Ha can be one- or two-sided (p1 ≠ p2, p1 > p2, p1 < p2). Under H0 you use the pooled proportion p̂c = (x1 + x2)/(n1 + n2) to compute the pooled standard error: SE = sqrt[p̂c(1−p̂c)(1/n1 + 1/n2)]. Check independence (two independent random samples or experiment + 10% for each) and success–failure using the pooled counts: n1p̂c, n1(1−p̂c), n2p̂c, n2(1−p̂c) ≥ 5 (or 10). AP tip: the CED expects a two-sample z-test for comparing proportions (Topic 6.10). Review pooled/stat formula and conditions at the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and practice problems (https://library.fiveable.me/practice/ap-statistics).
When do I use a two-sample z-test for difference of proportions vs other tests?
Use the two-sample z-test for the difference of two population proportions when you have two independent random samples (or a randomized experiment) and you want to test H0: p1 = p2 (or p1 − p2 = 0). Under H0 you use the pooled proportion p̂c = (x1 + x2)/(n1 + n2) to compute the pooled standard error and z statistic. Before using the test check the CED conditions: independence (random samples, 10% rule when sampling without replacement) and approximate normality via the success–failure condition using the pooled p̂c—i.e., n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) all ≥ about 5 (or 10 for stricter practice). When not to use it: if samples aren’t independent, counts are small (use Fisher’s exact or exact methods), or you’re doing one proportion (use one-sample z-test) or comparing many categories (chi-square). For CI for p1 − p2 you use the two-sample z-interval formula (unpooled SE). For more AP-aligned detail and examples see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and the Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6). For extra practice try the problems at (https://library.fiveable.me/practice/ap-statistics).
I'm confused about the pooled proportion formula - how do I calculate p̂c?
p̂c (the pooled proportion) is the combined estimate of the common proportion under H₀: p₁ = p₂. Compute it two equivalent ways: - p̂c = (n₁·p̂₁ + n₂·p̂₂) / (n₁ + n₂) - or, if you know counts of successes, p̂c = (X₁ + X₂) / (n₁ + n₂) You use p̂c when doing a two-sample z-test for p₁ − p₂ because under the null you assume the two populations have the same p, so you pool the data to estimate that common p. Then the pooled standard error is sqrt[ p̂c(1−p̂c) (1/n₁ + 1/n₂) ] and z = (p̂₁ − p̂₂) / (pooled SE). Don’t forget the AP conditions: samples independent, 10% rule if sampling without replacement, and the success–failure checks using p̂c (n₁p̂c, n₁(1−p̂c), n₂p̂c, n₂(1−p̂c) ≥ 5 or 10). See the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6) for examples and practice (https://library.fiveable.me/practice/ap-statistics).
What does it mean when the null hypothesis is p₁ - p₂ = 0?
H₀: p₁ − p₂ = 0 means you’re claiming the two population proportions are equal—there’s no difference or effect between group 1 and group 2. In practice that means your test is set up so the center of the sampling distribution for p̂₁ − p̂₂ is 0 under the null. For AP Stats you’d use a two-sample z-test for proportions (CED VAR-6.I.1), compute the pooled proportion p̂c = (X₁+X₂)/(n₁+n₂) when assuming H₀, and use the pooled standard error √[p̂c(1−p̂c)(1/n₁ + 1/n₂)] to get the z statistic. Before you trust the z test, check independence (random, independent samples and 10% rule) and the success–failure condition using n₁p̂c, n₁(1−p̂c), n₂p̂c, n₂(1−p̂c) ≥ 5 or 10 (CED VAR-6.J). For a quick refresher on setup and pooled SE, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP). If you want practice problems, Fiveable also has lots at (https://library.fiveable.me/practice/ap-statistics).
How do I check the conditions for a two-sample proportion test step by step?
Step-by-step check for a two-sample z-test for p1 − p2 (assume H0: p1 = p2): 1. State H0 and Ha. For example H0: p1 − p2 = 0 (p1 = p2). Choose one- or two-sided Ha (p1 > p2, p1 < p2, or p1 ≠ p2). 2. Independence: confirm data come from two independent random samples or a randomized experiment. If sampling without replacement, check each sample size ≤ 10% of its population (n1 ≤ 0.10N1 and n2 ≤ 0.10N2). 3. Pooled proportion (use for the test): p̂c = (x1 + x2) / (n1 + n2), where x1 = n1·p̂1 and x2 = n2·p̂2. 4. Success–failure (normality): compute n1·p̂c, n1·(1−p̂c), n2·p̂c, n2·(1−p̂c). Each should be ≥ the rule-of-thumb (commonly 5, sometimes 10) so the sampling distribution of p̂1 − p̂2 is approximately normal. 5. If all checks pass, use z = (p̂1 − p̂2 − 0) / sqrt[p̂c(1−p̂c)(1/n1 + 1/n2)] to get p-value. If not, use a simulation/bootstrap or exact method. For AP alignment and examples, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6). Practice more problems at (https://library.fiveable.me/practice/ap-statistics).
Why do we need to check that n₁p̂c ≥ 5 and all those other conditions?
You check n₁p̂c, n₁(1−p̂c), n₂p̂c, n₂(1−p̂c) ≥ 5 (or ≥10) because the two-sample z-test for p₁−p₂ relies on the sampling distribution being approximately normal. Under H₀: p₁ = p₂ you pool the samples to get p̂c = (n₁p̂₁ + n₂p̂₂)/(n₁ + n₂); pooling gives the best estimate of the common proportion and sets the correct standard error for the z statistic. If any of those counts are too small, the normal approximation is poor and the z-test (and its p-value) can be misleading. You also must check independence: samples should be random/independent and, when sampling without replacement, n ≤ 10% of the population (for each sample). These checks are required by the CED (VAR-6.J) for valid inference on the AP exam. For a quick refresher and examples, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and try practice questions (https://library.fiveable.me/practice/ap-statistics).
What's the formula for the two-sample z-test for difference of proportions?
Use a two-sample z-test for proportions when you want to test H0: p1 = p2 (or p1 − p2 = 0). Under H0 you pool the samples: - pooled proportion: p̂c = (x1 + x2) / (n1 + n2), where x1 = n1 p̂1 and x2 = n2 p̂2. - pooled standard error: SE = sqrt[ p̂c(1 − p̂c) (1/n1 + 1/n2) ]. - test statistic: z = (p̂1 − p̂2) / SE (since H0 assumes difference = 0). Also check conditions from the CED: independent random samples (and 10% rule when sampling without replacement) and success–failure using the pooled proportion: n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) should be ≥ 5 (or ≥10 if your teacher wants the stricter rule) so the sampling distribution is approximately normal. For more AP-aligned review see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and the Unit 6 page (https://library.fiveable.me/ap-statistics/unit-6). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
When do I write Ha: p₁ > p₂ vs Ha: p₁ ≠ p₂ in my alternative hypothesis?
Pick Ha based on the question you’re trying to answer—the alternative should match the claim or research question. - If you want to detect any difference (either group could be higher), use two-sided: Ha: p1 ≠ p2. This is common on the exam when they ask “different” or don’t indicate direction (CED VAR-6.H.3). - If you have a directional claim (you expect one proportion to be larger or smaller), use one-sided: Ha: p1 > p2 or Ha: p1 < p2. Use Ha: p1 > p2 when you’re testing whether population 1’s success rate is greater than population 2’s (CED VAR-6.H.3). - Don’t pick direction after seeing data—the direction must be decided before collecting/analyzing data. Also remember the null is H0: p1 = p2 (or p1 − p2 = 0) and, for a two-sample z-test, you’ll use the pooled proportion when H0 is assumed (CED VAR-6.H.1, VAR-6.I.1, VAR-6.J.1b). For a quick review on wording and examples, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP). For more practice, Fiveable has lots of practice questions (https://library.fiveable.me/practice/ap-statistics).
I don't understand what "independent random samples" means for proportion tests.
“Independent random samples” means the two groups you compare were chosen separately so one sample doesn’t affect the other. For a two-sample z-test for p1 − p2 the CED requires either (a) two independent random samples from each population or (b) a randomized experiment that assigns units to two treatments. Practically that means you didn’t sample the same people twice (paired data) and you didn’t pick one sample based on the other. Why it matters: the standard error formula and pooled proportion (p̂c = (x1+x2)/(n1+n2)) assume independence. If samples aren’t independent you must use a paired method or a different test. Also check the 10% condition when sampling without replacement (n1 ≤ 10% N1 and n2 ≤ 10% N2) and the success–failure checks (n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) ≥ 5 or 10) for approximate normality, per the CED. Want more practice or a quick refresher? See the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and thousands of practice problems (https://library.fiveable.me/practice/ap-statistics).
How do I know if my sample sizes are big enough for the normal approximation?
Check two things. First, independence: your data must come from two independent random samples or a randomized experiment, and if sampling without replacement each sample size should be ≤10% of its population (the 10% condition). Second, the sampling distribution must be approximately normal (success–failure condition). For a two-sample test you use the pooled proportion under H0: p̂c = (n1 p̂1 + n2 p̂2)/(n1 + n2). Then check that all four counts n1 p̂c, n1(1−p̂c), n2 p̂c, and n2(1−p̂c) are ≥ a cutoff (AP uses “typically 5 or 10”—many teachers use ≥5; some prefer ≥10 for extra caution). If they’re met, the two-sample z-test (pooled z) is OK; if not, don’t rely on the normal approx. For a quick refresher see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and other Unit 6 resources (https://library.fiveable.me/ap-statistics/unit-6). For extra practice try the AP question bank (https://library.fiveable.me/practice/ap-statistics).
What's the 10% rule and why do I need to check n₁ ≤ 10% N₁?
The 10% rule is a quick check for independence when you sample without replacement: each sample size should be no more than 10% of its population (n₁ ≤ 0.10·N₁ and n₂ ≤ 0.10·N₂). Why? When you remove many units from a finite population, later draws aren’t independent of earlier ones. If each sample is ≤10% of the population, the dependence is negligible and you can treat observations as (approximately) independent—an AP requirement for inference (CED VAR-6.J.1.a.ii). On the AP exam you must verify independence before using the two-sample z-test for proportions. If you can’t meet the 10% rule, you either use sampling with replacement, adjust variance with a finite-population correction, or acknowledge the independence issue and avoid standard z-methods. For more on checks and the pooled-proportion z-test, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and grab extra practice at (https://library.fiveable.me/practice/ap-statistics).
Can someone explain what pooled proportion means and why we use it?
Pooled proportion is the single best estimate of the common population proportion you assume under the null H0: p1 = p2. You compute it as p̂c = (x1 + x2) / (n1 + n2) (equivalently (n1 p̂1 + n2 p̂2)/(n1 + n2)). We use p̂c when doing a two-sample z-test for p1 − p2 because the null says both populations share one p, so the standard error should be based on that common value. The pooled standard error is sqrt[p̂c(1−p̂c)(1/n1 + 1/n2)] and the z statistic is (p̂1 − p̂2)/SEpooled. Why this matters for AP: the CED requires you to assume p1 = p2 under H0 and to check the success–failure condition using the pooled count (n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) ≥ 5 or 10). If those hold and samples are independent (and ≤10% rule if without replacement), the pooled z-test is appropriate. For a refresher, see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP). For more review and lots of practice problems, check the Unit 6 page (https://library.fiveable.me/ap-statistics/unit-6) and the practice bank (https://library.fiveable.me/practice/ap-statistics).
I keep getting confused about when to use pooled vs unpooled - which one is for proportion tests?
Use pooled when you’re doing a hypothesis test that assumes the two population proportions are equal under H₀ (H₀: p₁ = p₂ or p₁ − p₂ = 0). In that case you combine successes to get the pooled proportion p̂c = (x₁ + x₂)/(n₁ + n₂), use p̂c in the success–failure check (n₁p̂c, n₁(1−p̂c), n₂p̂c, n₂(1−p̂c) ≥ 5 or 10) and in the pooled SE: sqrt[p̂c(1−p̂c)(1/n₁ + 1/n₂)]. That’s the AP-approved approach for two-sample z-tests (CED VAR-6.I/J). Use the unpooled (separate p̂₁ and p̂₂) when you’re building a confidence interval for p₁ − p₂ or when the test does NOT assume p₁ = p₂—CIs always use the separate SE: sqrt[ p̂₁(1−p̂₁)/n₁ + p̂₂(1−p̂₂)/n₂ ]. Also always check independence (random/independent samples and 10% condition). For a quick review see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and practice questions (https://library.fiveable.me/practice/ap-statistics).
How do I write the hypotheses if I want to test whether one proportion is greater than another?
Pick an order for your groups (call them p1 = proportion for group 1, p2 = proportion for group 2). For a one-sided test that group 1 has a larger proportion than group 2 you write: H0: p1 = p2 (equivalently p1 − p2 = 0) Ha: p1 > p2 (equivalently p1 − p2 > 0) This is a one-sided (right-tailed) two-sample z-test for proportions. Under H0 you’ll use the pooled proportion p̂c = (x1 + x2)/(n1 + n2) to compute the standard error and z statistic. Before testing, check independence (random/independent samples and 10% condition) and the success–failure condition using the pooled counts (n1 p̂c, n1(1−p̂c), n2 p̂c, n2(1−p̂c) usually ≥ 10). For AP-aligned review and examples see the Topic 6.10 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-difference-two-population-proportions/study-guide/sJt2F9NwsQ2gihYEHGjP) and extra practice (https://library.fiveable.me/practice/ap-statistics).