Remember from previous sections that in statistics, a parameter is a numerical value that describes a characteristic of a population or the distribution of a random variable. It's a fixed value that is used to describe or summarize a population or sample. For example, the mean of a population is a parameter, as it describes the central tendency of the population. The standard deviation of a population is another example of a parameter, as it describes the spread or dispersion of the population.
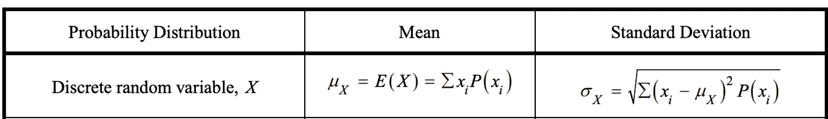

Center of a Discrete Random Variable
The mean or expected value of a discrete random variable is a measure of the central tendency of the variable. It represents the average outcome of the random variable over many repetitions of the same chance process.
To find the mean or expected value of a discrete random variable, X, you need to multiply each possible value of X by its probability and then add all of the products. This is often represented by the following formula:
E(X) = ∑x * P(X=x), where E(X) is the expected value of X, ∑x is the sum of all possible values of X, and P(X=x) is the probability of X being equal to x.
For example, if you have a discrete random variable X with two possible values, x1 and x2, and probabilities P(X=x1) and P(X=x2), respectively, then the mean or expected value of X would be:
E(X) = x1 * P(X=x1) + x2 * P(X=x2)
This gives you the average outcome of the random variable over many repetitions of the same chance process.
When calculating the mean or expected value of a discrete random variable, it is important to remember that the result is almost always a decimal value. This is because the probability of each possible value of the random variable is typically a decimal value.
For example, if you have a discrete random variable X with three possible values, x1, x2, and x3, and probabilities P(X=x1), P(X=x2), and P(X=x3), respectively, then the mean or expected value of X would be:
E(X) = x1 * P(X=x1) + x2 * P(X=x2) + x3 * P(X=x3)
If any of the probabilities, P(X=x1), P(X=x2), or P(X=x3), are decimals, then the expected value, E(X), will also be a decimal.
It is important to remember to write the expected value as a decimal, rather than rounding it to the nearest integer, as this can significantly affect the accuracy of your results.
Variability of a Discrete Random Variable
The standard deviation of a discrete random variable is a measure of the dispersion or spread of the variable's values around the mean. It tells you how much the values of the variable typically vary from the mean.
The variance of a discrete random variable, X, is a measure of the spread of the variable's values around the mean. It is calculated by taking the sum of the squares of the differences between each possible value of the variable and the mean, weighted by their probabilities. This is often represented by the following formula:
Var(X) = ∑(x - E(X))^2 * P(X=x), where Var(X) is the variance of X, ∑ is the sum of all possible values of X, E(X) is the mean or expected value of X, x is a possible value of X, and P(X=x) is the probability of X being equal to x.
The standard deviation of X is the square root of the variance, and is often represented by the following formula:
SD(X) = √Var(X), where SD(X) is the standard deviation of X and Var(X) is the variance of X.
So, to calculate the standard deviation of a discrete random variable, X, you would first calculate the variance using the formula above, and then take the square root of the variance to get the standard deviation. The standard deviation tells you how much the values of the variable typically vary from the mean, and a smaller standard deviation indicates that the values are more closely clustered around the mean, while a larger standard deviation indicates that the values are more spread out.
💡 AP tip: If you decide to use your calculator, make sure you list how you got to your answer. Use context and don’t just put a number down as the answer. Show work to maximize the amount of points you get.
🎥 Watch: AP Stats - Probability: Random Variables, Binomial/Geometric Distributions
Practice Problem
A random variable, X, represents the number of text messages a person receives in a day. The probability distribution of X is shown in the table below:

(a) Calculate the mean or expected value of X.
(b) Calculate the variance of X.
(c) Calculate the standard deviation of X.
(d) Interpret the results in the context of the problem.
Answer
To solve this problem, you would need to use the formulas for calculating the mean, variance, and standard deviation of a discrete random variable.
(a) To calculate the mean or expected value of X, you would need to multiply each possible value of X by its probability and then add all of the products. Using the formula E(X) = ∑x * P(X=x), you would get:
E(X) = (0 * 0.2) + (1 * 0.3) + (2 * 0.4) + (3 * 0.1) = 1.4
So, the mean or expected value of X is 1.4.
(b) To calculate the variance of X, you would need to take the sum of the squares of the differences between each possible value of the variable and the mean, weighted by their probabilities. Using the formula Var(X) = ∑(x - E(X))^2 * P(X=x), you would get:
Var(X) = (0 - 1.4)^2 * 0.2 + (1 - 1.4)^2 * 0.3 + (2 - 1.4)^2 * 0.4 + (3 - 1.4)^2 * 0.1 = 1.02
So, the variance of X is 1.02.
(c) To calculate the standard deviation of X, you would need to take the square root of the variance. Using the formula SD(X) = √Var(X), you would get:
SD(X) = √1.02 = 1.00995049
So, the standard deviation of X is 1.01.
(d) The mean or expected value of X is 1.4, which tells us that, on average, a person receives 1.4 text messages per day. The variance of X is 1.02, which tells us that the values of X tend to vary somewhat from the mean. The standard deviation of X is 1.01, which tells us that the values of X tend to be relatively closely clustered around the mean. This suggests that the number of text messages a person receives in a day tends to be relatively consistent, with relatively few extreme deviations from the mean.
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| discrete random variable | A random variable that takes on a countable number of distinct values, often representing counts or categorical outcomes. |
| expected value | The long-run average outcome of a random variable, equivalent to the mean of a discrete random variable. |
| mean | The average value of a dataset, represented by μ in the context of a population. |
| parameter | A numerical summary that describes a characteristic of an entire population. |
| standard deviation | A measure of how spread out data values are from the mean, represented by σ in the context of a population. |
Frequently Asked Questions
How do I calculate the mean of a discrete random variable?
The mean (expected value) of a discrete random variable X is a weighted average of its possible values: μX = E(X) = Σ xi · P(xi). That means multiply each outcome xi by its probability, add those products, and that sum is the long-run average you’d expect if you repeated the random process many times. Include units (dollars, people, minutes) when you interpret the result. Quick notes for AP: the formula μX = Σ xiP(xi) and the variance/SD formulas appear on the AP formula sheet (CED Topic 4.8, VAR-5.C). For common distributions there are shortcuts—e.g., if X ~ Binomial(n,p), μX = np (useful on the exam). Also remember linearity of expectation: E(a + bX) = a + bE(X). Want practice? Review the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px), the Unit 4 overview (https://library.fiveable.me/ap-statistics/unit-4), and try problems at (https://library.fiveable.me/practice/ap-statistics).
What's the formula for standard deviation of a random variable and why is there a square root?
The formula (from the CED) for the standard deviation of a discrete random variable X is σX = sqrt( Σ (xi − μX)^2 · P(xi) ), where μX = Σ xi · P(xi). That inside-sum is the variance, Var(X) = Σ (xi − μX)^2 P(xi). Why the square root? We square deviations so positive and negative differences don’t cancel and so larger gaps count more. Squaring gives a quantity in “squared” units (e.g., dollars^2), which is hard to interpret, so we take the square root to return to the original units. The standard deviation therefore measures typical distance (on the original scale) from the mean. On the AP exam you’ll see variance used in calculations but the formula sheet gives σX as the square root (Topic 4.8; it’s on the AP formula sheet). For a quick review see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px).
When do I use the expected value formula vs just finding the regular mean?
Use the expected-value formula when X is a random variable described by a probability model (a probability mass function) and you want the population parameter μX = E(X) = Σ xi·P(xi). That’s a weighted mean: each outcome xi gets weighted by its probability. Use the regular/sample mean x̄ = (1/n)Σ xi when you have actual observed data (a sample) and are summarizing those n values. Quick rules to remember (AP language from the CED): - If you’re given a probability distribution or a model (e.g., binomial, geometric), compute μX = Σ xiP(xi) or the shortcut μ = np for binomial. This gives a parameter for the random variable (VAR-5.C). - If you’re given a list of sample observations, compute x̄ = (Σ xi)/n—that’s a statistic estimating the population mean. Always interpret your answer in context with units and long-run meaning (VAR-5.D). For a refresher and examples, see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
I'm confused about what a parameter is - is it the same thing as a statistic?
Short answer: no—a parameter and a statistic are related but different. A parameter is a single fixed number that describes a population or a probability model (for Topic 4.8, μX and σX for a discrete random variable are parameters; see VAR-5.C.1–3). A statistic is a number calculated from a sample (like x̄ or s) and can vary from sample to sample. Example: the population mean μ (a parameter) is fixed but usually unknown. You estimate it with the sample mean x̄ (a statistic). On the AP exam you’ll need to calculate and interpret parameters for random variables (VAR-5.C) and know that parameters are the true, fixed values your sample statistics try to estimate. For a refresher on formulas and worked examples, check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px). For extra practice, use the AP practice bank (https://library.fiveable.me/practice/ap-statistics).
How do I know if I should interpret my answer in context or just give the number?
Short answer: follow the task verb. If the question asks you to "interpret," "explain," or is a free-response part that’s testing VAR-5.D, you must state the meaning in context with units. If it only asks you to "calculate" or it’s a multiple-choice numeric answer, the number (with units) is usually enough. How that looks in practice: - Calculation-only (Skill 3.B): Give the numeric parameter and units (e.g., μ = 2.4). - Interpretation (Skill 4.B / VAR-5.D): Write a sentence tying the parameter to the scenario and units. For a mean: “On average, we expect about 2.4 moviegoers (out of 3) to buy snacks if we repeat this selection many times.” For an SD: “A typical number of moviegoers differs from the mean by about 0.49 people (in the long run).” On the AP exam, pay attention to the verb (Calculate vs Interpret) and include context and units when asked (see Topic 4.8 study guide for examples) (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px). For more practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
What's the difference between population parameters and sample statistics for random variables?
Population parameters are the true, fixed numbers that describe a random variable’s distribution—think of the mean (expected value) μX and standard deviation σX for a discrete random variable. On the AP CED this is explicit: μX = Σ xi·P(xi) and σX = sqrt(Σ(xi − μX)^2·P(xi)) (VAR-5.C). Parameters are properties of the population or probability model, not something that varies from sample to sample. Sample statistics (x̄, s, p̂, etc.) are calculated from a particular sample and are estimates of those parameters. They vary from sample to sample; their sampling distributions (and standard errors) are what you use for inference (e.g., σx̄ = σ/√n). Remember: parameters = fixed (but usually unknown); statistics = computed, random, and used to estimate/test parameters (Skill 3.B, VAR-5.D). For a quick CED review, see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px). Want practice? Try problems at (https://library.fiveable.me/practice/ap-statistics).
Can someone explain step by step how to find the standard deviation using that long formula?
Start with the formula from the CED: σX = sqrt( Σ (xi − μX)^2 · P(xi) ). Step-by-step: 1. List outcomes xi and their probabilities P(xi). Example: x = {0,1,2} with P = {0.2, 0.5, 0.3}. 2. Compute the mean (expected value) μX = Σ xi·P(xi). For the example: μX = 0(0.2) + 1(0.5) + 2(0.3) = 1.1. 3. For each outcome, find the squared deviation: (xi − μX)^2. Example: (0−1.1)^2 = 1.21, (1−1.1)^2 = 0.01, (2−1.1)^2 = 0.81. 4. Multiply each squared deviation by its probability: (xi − μX)^2 · P(xi). Example: 1.21·0.2 = 0.242; 0.01·0.5 = 0.005; 0.81·0.3 = 0.243. 5. Sum those values to get the variance: Var(X) = Σ = 0.242+0.005+0.243 = 0.49. 6. Take the square root to get σX: σX = sqrt(0.49) = 0.7 (same units as X). Interpretation: σX measures typical distance of outcomes from the mean in the context (CED VAR-5.C.3, VAR-5.D.1). For more examples and practice, see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and extra practice problems (https://library.fiveable.me/practice/ap-statistics).
Why do we multiply each x value by its probability when finding the mean?
Think of the mean (expected value) of a random variable as the long-run average you'd get if you repeated the random process many times. Each possible outcome x happens with some chance P(x), so its contribution to the long-run average should be x times how often it occurs. Multiplying x by P(x) weights that outcome by its probability; summing those weighted values, μ = Σ x·P(x), gives the overall average you expect. This is exactly the “weighted mean” idea in the CED (VAR-5.C.2): outcomes are weighted by their probabilities. It also explains linearity of expectation: expectation of a sum = sum of expectations, because each outcome’s contribution is just its value times its chance. For more practice and AP-aligned explanation, see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and try binomial/expected-value problems in the practice set (https://library.fiveable.me/practice/ap-statistics).
I don't understand when to use mu vs x-bar notation - which one is for random variables?
Use mu (μ) when you’re talking about a population parameter or the mean of a random variable (a fixed number). Use x̄ when you’re talking about a sample statistic—the mean you actually calculate from data, which is a random variable because it changes from sample to sample. Quick rules tied to Topic 4.8 (CED): - For a discrete random variable X, its expected value is μX = Σ xi·P(xi) (that μ is a parameter—single fixed value). - If you draw a sample of size n, the sample mean x̄ is a statistic whose sampling distribution has mean μ and standard deviation σ/√n (or s/√n as the standard error). - Population SD uses σ (parameter); sample SD uses s (statistic/estimate). On the AP exam you’ll be expected to identify parameters vs. statistics and use the right formulas (they give formulas/tables; see the formula sheet in the CED). For a focused review, check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and try practice problems (https://library.fiveable.me/practice/ap-statistics) to get comfortable switching notation.
How do I solve a word problem asking for the expected value of something like lottery winnings?
Think of a lottery payout as a discrete random variable X with each possible dollar outcome x_i and its probability P(x_i). Use the AP formula: μX = Σ x_i·P(x_i) (VAR-5.C.2). Steps: 1. List all outcomes (including losing your ticket cost as a negative value) and their probabilities. 2. Multiply each dollar outcome by its probability. 3. Add those products—that sum is the expected value (mean) in dollars. 4. Interpret in context: it’s the long-run average payoff per ticket. Quick example: $1 ticket, win $1,000 with P = 0.0001, else get $0. Expected value = 1000(0.0001) + 0(0.9999) − 1 (ticket cost counted separately) = 0.1 − 1 = −0.90 dollars. So you lose on average $0.90 per ticket in the long run. For AP free-response, show the full calculation, include units, and give a context interpretation (long-run average). For more practice, check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and tons of practice problems (https://library.fiveable.me/practice/ap-statistics).
What does it mean to interpret parameters "within the context of a specific population"?
A parameter is a single, fixed number that describes a population or a random variable’s distribution (like μX or σX). Interpreting a parameter “within the context of a specific population” means you always state what population you're describing, use the correct units, and explain the practical meaning—not just the symbol. For example: “μX = 15.1 kg is the average weight of penguins in this population,” or “σX = 2.2 kg tells us how much penguin weights typically vary around that average.” On AP problems (VAR-5.D) you should: name the population, give the numerical parameter, include units, and explain in words what that number means in the long run or for that whole population. Want more examples and practice on mean/SD of discrete RVs? Check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and hit the unit page (https://library.fiveable.me/ap-statistics/unit-4) or practice problems (https://library.fiveable.me/practice/ap-statistics).
I keep getting confused about whether to use the parameter formulas or the sample formulas on the AP exam.
Use the parameter formulas when you’re working with a probability model or a population/random variable; use the sample formulas when you’re working with actual data from a sample. Quick rules you can rely on (CED language): - Random variable / distribution (parameter): mean μX = Σ xi·P(xi); variance σX^2 = Σ (xi − μX)^2·P(xi); SD σX = √(…). For binomial: μ = np and σ = √(np(1−p)). These are fixed parameters of the probability model (VAR-5.C). - Sample statistics (from data): x̄ = Σ xi / n and sample SD sx = √[Σ(xi − x̄)^2/(n−1)]. Use these when the problem gives raw/sample data and asks for a sample summary. - Sampling distributions: if you take sample means, μx̄ = μ and σx̄ = σ/√n (or use s/√n when σ unknown). On the exam you’ll be asked to identify when you’re dealing with a parameter vs a statistic (interpretation in context, VAR-5.D). AP expectation: when a problem describes a probability model (e.g., a binomial or given pmf) compute parameters using the parameter formulas; when it gives sample data compute x̄ and s (and note the formula sheet includes these). For more practice and examples see the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and unit review (https://library.fiveable.me/ap-statistics/unit-4). For lots of practice problems go to (https://library.fiveable.me/practice/ap-statistics).
How do I calculate the variance first and then find standard deviation, or can I skip that step?
You don’t have to do a separate algebraic “variance” step if you don’t want to, but conceptually the standard deviation comes from the variance, so you’ll compute that same quantity either way. Steps (AP CED formulas): 1. Find the mean (expected value) μ = Σ xi·P(xi). 2. Compute the variance σ² = Σ (xi − μ)²·P(xi). 3. Take the square root to get σ = √σ². You can combine steps 2–3 by computing Σ (xi − μ)²·P(xi) and immediately taking the square root—that’s still finding the variance first, just not writing it down separately. Why variance is useful: variance (units²) is how the SD is produced and helps with intermediate checks (e.g., if variance = 4 then σ = 2). For common distributions use the shortcut formulas (binomial: σ² = np(1−p), μ = np). The AP formula sheet gives these (Topic 4.8). For a quick topic review check the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the difference between finding the mean of data values vs finding the expected value of a random variable?
Short answer: they’re the same idea (an average) but different contexts and formulas. - Mean of data values (x̄) is a statistic computed from a specific sample: x̄ = (1/n) Σ xi. It summarizes observed values and can vary from sample to sample. On the AP exam this is treated as a sample summary (Unit 1/2 ideas). - Expected value (E[X] or μX) is the mean of a random variable—a population parameter defined by the probability model: μX = Σ xi·P(xi). It’s a weighted mean where each possible outcome is weighted by its probability (CED VAR-5.C.2). It doesn’t depend on one sample; it’s a fixed parameter of the distribution. Interpret μX in context with units and long-run/average language. Key points for AP: use x̄ for sample data, μX or E(X)=ΣxP(x) for random variables; variance/SD formulas differ accordingly (CED VAR-5.C.3). If you want extra practice, check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) and more problems (https://library.fiveable.me/practice/ap-statistics).
Why does the standard deviation formula have that (x - mu) squared part in it?
Good question—the (x − μ)² is there for two reasons: direction and weighting. First, deviations (x − μ) can be positive or negative, so if you just summed them they'd cancel out and give zero. Squaring makes all deviations positive, so you measure total spread. Second, squaring gives bigger weight to outcomes that are farther from the mean, which matches our idea of variability: big outliers should increase the spread more than tiny differences. That squared-average is the variance (σ² = Σ(x−μ)²·P(x)), and taking the square root brings the units back to the original (σ = sqrt(variance)), so standard deviation is in the same units as X and is easier to interpret in context. This matches the CED formulas for mean and SD of a discrete random variable (see Topic 4.8). For more practice and examples tied to the AP exam, check the Topic 4.8 study guide (https://library.fiveable.me/ap-statistics/unit-4/mean-standard-deviation-random-variables/study-guide/g1wJm2o6V4wCoqbsC5Px) or Unit 4 overview (https://library.fiveable.me/ap-statistics/unit-4).