

Hypotheses
When it has been identified that we need to perform a one-proportion z-test for a population proportion, the first step we need to do is write out our hypotheses. We have two hypotheses to write: our null hypothesis and our alternative hypothesis.
(1) Null ("H0")
In a statistical hypothesis test, our null hypothesis is the hypothesis based on our claim that was given in the problem. The null hypothesis is a statement about the population parameter that is being tested. It is the situation that is assumed to be true unless there is evidence to the contrary. The null hypothesis is usually a statement of no difference or no relationship between variables. The null is always written as p =____.
For example, if the null hypothesis is that the population proportion is 0.5, this means that it is assumed to be true that the population proportion is 0.5 (p = 0.5) unless there is evidence to the contrary. If the sample proportion is significantly different from 0.5, this would provide evidence against the null hypothesis and suggest that the population proportion is not 0.5.
Remember, if our null hypothesis is true, there is no wow factor, nothing new to claim and essentially, it appears that the original claim was true.
(2) Alternative ("Ha")
Our alternate hypothesis is the hypothesis that the claim in our null is not true. It is always written as either p <____, p >____ or p ≠_____. The alternative hypothesis is usually a statement of difference or relationship between variables. If we are testing that the actual proportion is less than or greater than the claimed proportion, we are doing a one tailed z-test. If we are testing that the actual proportion is not equal to the claimed proportion, we are doing a two tailed z-test.
If the evidence supports the alternative hypothesis, the null hypothesis is rejected in favor of the alternative hypothesis. If the evidence does not support the alternative hypothesis, the null hypothesis is not rejected.
SUMMARY:
- For hypotheses about parameters, the null hypothesis contains an equality reference (=, ≥, or ≤), while the alternative hypothesis contains a strict inequality (<, >, or ≠). The type of inequality in the alternative hypothesis is based on the question of interest.
- Alternative hypotheses with < or > are called one-sided, and alternative hypotheses with ≠ are called two-sided. Although the null hypothesis for a one-sided test may include an inequality symbol, it is still tested at the boundary of equality.
Example
An article recently published in Real News Online! states that 94% of all people can identify the pop culture icon, Baby Yoda. To test this claim, we poll a random sample of 750 people and find that 700 of them can correctly identify Baby Yoda. Do the data give significant evidence that the actual proportion of people who can identify Baby Yoda is more than 94%?
For this question, we are clearly testing a population claim using the sample that we have collected. This calls for a one sample z test for population proportion (or 1-Prop Z Test). Our first step is to write our hypotheses:
- H0: p = 0.94
- Ha: p < 0.94
Conditions
Random
As with any hypothesis test or confidence interval, we must have a random sample to perform our test. If we do not have a random sample, we can not infer anything about the population because our sample might be biased. There is no way to fix sampling bias using mathematical calculations. If our sample is biased, the whole study might as well be thrown out.
Independent
Since we are sampling without replacement, we need to make sure that our population is large enough that our experimental units is not really affecting each other after they are selected. To be sure of this, we can use the 10% condition, which states that the population should be at least 10 times the size of the sample. To show this, we can state: "Since it is reasonable to believe that our population is at least 10n, we can assume our sample is independent.
Normal
Since we will be using the normal curve to calculate the probability of obtaining our sample, we must first prove that the sampling distribution is normal. For proportions, we will use the Large Counts Condition, which states the expected numbers of successes and failures is at least 10.
Example
In our example above, we would check the three conditions like this:
- Random: "we poll a random sample of 750 people"
- Independent: It is reasonable to believe that there are at least 7500 people in the world (obviously true!)
- Normal: 750 (0.94) = 658, 750 (0.06) = 45. Both 658 and 45 are more than 10, so we're good.
Calculating Our Necessary Statistics
For actually calculating the values associated with our test, we have to calculate our critical value and from that, we can calculate our p-value.
Z-Score
The z-score for our data is based on the standard normal curve for our sampling distribution. In other words, we are going to see where our sample falls in the range of all possible samples of size n.
.png&w=828&q=75)
For our example above, our observed value was 0.93333. Our expected value was 0.94.
Our standard deviation is calculated just like that of a sampling distribution:
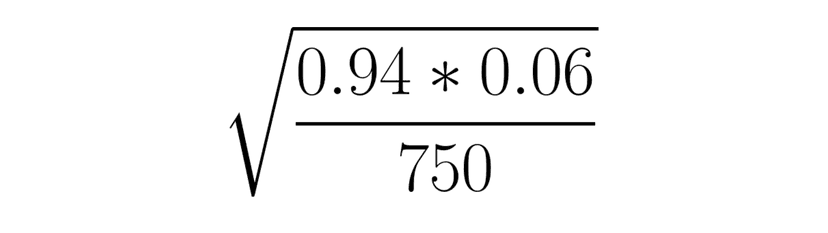
which comes out to be 0.00867.
Putting it all together, our z score comes out to be -0.769.
P-Value
To calculate our p-value, we are going to use our z-score and see the probability of obtaining that sample by using the standard normal curve and calculating the probability of receiving such a z-score (or higher/lower).
For the example above, we would use our z-score of -0.769 and find the probability of receiving that (or something lower). One way to do this is to use a calculator with the normalcdf function.
Calculating our p-value with this z-score would look like this:
normalcdf(-100000, -0.769, 0, 1) = 0.221.
Using Technology
If this sounds like a lot of work for one problem, you're in luck!
Our graphing calculator will do all of this for us! We just need to go to the Stats Tests Menu and select 1-Prop Z-Test. From there, we simply enter in our parameters and our calculator will give us a z-score and p-value automatically!
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| 10% condition | The requirement that sample size n is at most 10% of the population size N to ensure independence when sampling without replacement. |
| alternative hypothesis | The claim that contradicts the null hypothesis, representing what the researcher is trying to find evidence for. |
| approximately normal | A distribution that closely follows the shape of a normal distribution, allowing for the use of normal probability methods. |
| categorical variable | A variable that takes on values that are category names or group labels rather than numerical values. |
| independence | The condition that observations in a sample are not influenced by each other, typically ensured through random sampling or randomized experiments. |
| null hypothesis | The initial claim or assumption being tested in a hypothesis test, typically stating that there is no effect or no difference. |
| number of failures | The count of unfavorable outcomes in a sample, denoted as n(1-p̂), used to verify the normality condition. |
| number of successes | The count of favorable outcomes in a sample, denoted as np̂, used to verify the normality condition. |
| one-sample z-test for a population proportion | A hypothesis test used to determine whether a sample proportion provides evidence that a population proportion differs from a hypothesized value. |
| one-sided alternative hypothesis | An alternative hypothesis that specifies the direction of the difference, either p₁ < p₂ or p₁ > p₂. |
| population proportion | The true proportion or percentage of a characteristic in an entire population, typically denoted as p. |
| random sample | A sample selected from a population in such a way that every member has an equal chance of being chosen, reducing bias and allowing for valid statistical inference. |
| randomized experiment | A study design where subjects are randomly assigned to treatment groups to establish cause-and-effect relationships. |
| sample proportion | The proportion of individuals in a sample that have a particular characteristic, denoted as p-hat (p̂). |
| sampling distribution | The probability distribution of a sample statistic (such as a sample proportion) obtained from repeated sampling of a population. |
| sampling without replacement | A sampling method in which an item selected from a population cannot be selected again in subsequent draws. |
| statistical inference | The process of drawing conclusions about a population based on data collected from a sample. |
| two-sided alternative hypothesis | An alternative hypothesis that specifies the difference could be in either direction, stated as p₁ ≠ p₂. |
Frequently Asked Questions
How do I set up null and alternative hypotheses for population proportion problems?
Start by writing the null as the “no-effect” value and put the equality there: H0: p = p0 (p0 is the claimed population proportion). The alternative is what you want to gather evidence for and uses a strict inequality: - one-sided (greater): Ha: p > p0 (testing if proportion is larger) - one-sided (less): Ha: p < p0 (testing if proportion is smaller) - two-sided: Ha: p ≠ p0 (testing for any difference) Remember the CED rule: the null contains the equality; the alternative is strict. For a one-sample z-test for a proportion use H0: p = p0 and check conditions assuming H0 is true: independence (random sample and n ≤ 10% of population) and success–failure np0 ≥ 10 and n(1 − p0) ≥ 10 so the sampling distribution of p̂ is approximately normal. For a quick topic review see the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). For practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
What's the difference between one-sided and two-sided alternative hypotheses?
Short answer: the alternative (Ha) is one-sided when you're testing for a change in a specific direction (Ha: p > p0 or Ha: p < p0). It’s two-sided when you’re testing for any difference (Ha: p ≠ p0). Details that matter for AP Stats (CED VAR-6.D): - The null always contains the equality (H0: p = p0). The alternative uses a strict inequality (<, >, ≠). - One-sided tests (>, <) look for evidence in one direction only; two-sided (≠) checks both directions. - Even if H0 is written with ≥ or ≤ for a one-sided test, you still evaluate the test at the equality boundary (p = p0). - For one-sample z-tests for a proportion you use p0 to compute the standard error and check np0 and n(1−p0) ≥ 10 plus independence (n ≤ 10% N or random sampling) before using the normal model. If you want a quick AP-aligned refresher, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and try practice questions (https://library.fiveable.me/practice/ap-statistics).
When do I use a one-sample z-test for proportions vs other tests?
Use a one-sample z-test for a proportion when you’re testing a single population proportion (H0: p = p0) and the AP conditions are met. Specifically: - The question is about one categorical variable (one population proportion). - Independence: data from a random sample or randomized experiment and, if sampling without replacement, n ≤ 10% of the population. - Success–failure (normal approx): under H0 use p0 to check np0 ≥ 10 and n(1 − p0) ≥ 10. That lets you use the normal model and compute z = (p̂ − p0)/√[p0(1−p0)/n]. - Choose Ha as one-sided (p < p0 or p > p0) or two-sided (p ≠ p0) based on the research question. If the success–failure condition fails (small counts), use an exact binomial test or a simulation-based method instead. For AP-aligned review, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT), the Unit 6 overview (https://library.fiveable.me/ap-statistics/unit-6), and practice problems (https://library.fiveable.me/practice/ap-statistics).
What are the conditions I need to check before doing a proportion test?
Before you run a one-sample z-test for a proportion, check these AP-approved conditions (CED VAR-6.F): - Independence: data come from a random sample or randomized experiment. If sampling without replacement, make sure n ≤ 10% of the population (the 10% condition). - Normality (success–failure): assuming H0 is true (p = p0), verify np0 ≥ 10 and n(1 − p0) ≥ 10 so the sampling distribution of p̂ is approximately normal. - State hypotheses correctly first: H0: p = p0 and Ha: p < p0, p > p0, or p ≠ p0 (one-sided or two-sided per VAR-6.D). If these fail (small counts or nonrandom sample), use a simulation or exact methods instead. For a quick review of this Topic 6.4 checklist, see the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). For more practice, try problems at https://library.fiveable.me/practice/ap-statistics.
I'm confused about when to write Ha: p > p0 versus Ha: p ≠ p0 - how do I know which one?
Pick the alternative that matches the claim you’re trying to test. H0 always has the equals form H0: p = p0. The alternative is where you put the strict inequality: - If the question (or claim) says “more than,” use Ha: p > p0. - If it says “less than,” use Ha: p < p0. - If it says “different from,” “not equal to,” or just asks whether there’s any difference, use Ha: p ≠ p0 (two-sided). Remember AP language from the CED: the alternative must be a strict inequality and reflects the evidence you want to collect (VAR-6.D.1–4). Also when you run the one-sample z test, check conditions assuming H0 (use p0 for the success–failure np0 ≥ 10 rule) and report the p-value appropriately. For a quick refresher, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the formula for checking if np0 and n(1-p0) are both at least 10?
You check the success–failure condition using the null proportion p₀ and your sample size n: - Number of expected successes: np₀ ≥ 10 - Number of expected failures: n(1 − p₀) ≥ 10 If both hold (and independence/10% condition and random sampling are satisfied), the sampling distribution of p̂ is approximately normal and you can use the one-sample z-test for a proportion (CED VAR-6.F.1.b). The null hypothesis you use for the test is H₀: p = p₀ (VAR-6.D.3). For a quick review of this setup and examples, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). For broader unit review and lots of practice problems, check Unit 6 (https://library.fiveable.me/ap-statistics/unit-6) and the practice bank (https://library.fiveable.me/practice/ap-statistics).
How do I know what value to use for p0 in my null hypothesis?
Pick p0 from the claim or status quo you’re testing—it’s the proportion value you assume true unless data say otherwise. On the AP, the null for a proportion is written H0: p = p0 (CED VAR-6.D.3). Typical choices for p0 are: - a previously reported proportion (e.g., “last year 0.45”), - a legal/benchmark value (e.g., 0.50 for “no preference”), or - the value in the research claim you want to test (the “no effect” or status-quo value). Remember: the sampling-distribution checks use p0, not p̂. For the success–failure condition assume H0 true and verify np0 ≥ 10 and n(1−p0) ≥ 10 (CED VAR-6.F.1.b). Also confirm independence (random sample, n ≤ 10% of population) before using the one-sample z-test for a proportion (CED VAR-6.E.1 and VAR-6.F.1.a). For more examples and practice, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
Can someone explain step by step how to verify all the conditions for a proportion test?
Start by writing the hypotheses: H0: p = p0 and choose Ha (p < p0, p > p0, or p ≠ p0) based on the question (one-sided vs two-sided). Then check the two inference conditions from the CED: 1) Independence - Was the data from a random sample or randomized experiment? If yes, independence is likely. - If sampling without replacement, verify n ≤ 10% of the population (10% condition). If this fails, you can’t assume independence. 2) Normal approximation (success–failure) - Under H0, use p0 to check np0 ≥ 10 and n(1 − p0) ≥ 10. If both hold, the sampling distribution of p̂ is approximately normal and you can use the one-sample z-test for a proportion (SE = sqrt[p0(1−p0)/n]). If either condition fails, use an exact (binomial) test or a simulation-based method. For AP-aligned review, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and practice questions (https://library.fiveable.me/practice/ap-statistics).
What does it mean that the null hypothesis is "tested at the boundary of equality" for one-sided tests?
When the CED says a one-sided null is “tested at the boundary of equality,” it means you treat H0 as the exact value p = p0 when you compute the test statistic, standard error, and check conditions—even if H0 is written with ≥ or ≤. Practically that means: - Your test uses p0 (not p̂) for the SE: SE = sqrt[p0(1−p0)/n]. - The success–failure check uses np0 and n(1−p0) ≥ 10 to justify the normal approximation. - The z statistic is (p̂ − p0)/SE, and the p-value is from the appropriate one-sided tail. This follows VAR-6.D.2 and VAR-6.F.1 in the CED: the null contains the equality and we assume p = p0 when deriving sampling behavior. For a quick refresher on setup and examples, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). For more practice, try the AP practice problems (https://library.fiveable.me/practice/ap-statistics).
I don't understand the 10% rule - when do I need to check that n ≤ 10% of N?
You check the 10% rule any time your data come from sampling without replacement (you’re taking distinct people/items from a finite population). The CED says this is part of verifying independence for inference—when sampling without replacement, you should confirm n ≤ 0.10N. That means your sample size n must be no more than 10% of the population size N (e.g., if N = 5,000, you want n ≤ 500). If you used a randomized experiment or sampling with replacement, the 10% rule isn’t needed for independence. If n > 0.10N when sampling without replacement, observations aren’t independent and the usual standard errors can be too small—be cautious or use methods that account for the finite population. For AP exam prep, remember to state you checked independence and cite the 10% condition when relevant (see the Topic 6.4 study guide for more: https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
A company claims 85% of customers are satisfied but I think it's lower - how do I write my hypotheses?
Write the hypotheses like this: H0: p = 0.85 Ha: p < 0.85 Why: the company’s claim (85% satisfied) is the null value p0—the null always includes the equality (CED VAR-6.D.3). Your belief it’s lower makes the alternative one-sided with a “<” (CED VAR-6.D.2–4). For testing you’d use a one-sample z-test for a proportion (CED VAR-6.E.1), but before that check conditions: random/independent sample (and n ≤ 10% of population if sampling without replacement) and the success–failure condition using p0: np0 ≥ 10 and n(1−p0) ≥ 10 (CED VAR-6.F.1). Want a quick refresher? See the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
Why do we assume the null hypothesis is true when checking the normality condition?
When you set up a one-sample z-test for a proportion, the null hypothesis gives a specific value p0 for the population proportion (H0: p = p0). To check the sampling distribution’s shape you need a concrete value to compute expected counts of successes and failures. That’s why the AP CED asks you to check np0 and n(1 − p0) ≥ 10—you’re evaluating the success–failure condition under the assumption H0 is true so you can decide whether the normal approximation to p̂ is appropriate. If you used p̂ instead, you'd be checking a different model (closer to a CI), and your test’s standard error and p-value would be inconsistent with the hypothesis you’re testing. Bottom line: assume H0 true to verify the test’s conditions and use the correct standard error for the z statistic. For the CED details see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT). Need practice applying this? Try AP practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the difference between H0: p = 0.5 and H0: p ≥ 0.5 and which one should I use?
Use H0: p = 0.5. The CED says the null for a proportion must specify an equality (H0: p = p0) because the test is done at that boundary value. H0: p ≥ 0.5 is not the standard form you’d write for a single-sample z-test—the null should be p = 0.5 and the alternative expresses the question of interest: - If you want to test “more than 50%,” use Ha: p > 0.5 and H0: p = 0.5. - If you want to test “less than 50%,” use Ha: p < 0.5 and H0: p = 0.5. - If you want to test “different from 50%,” use Ha: p ≠ 0.5 and H0: p = 0.5. Also remember AP requirements: when checking normal approximation for the one-sample z test use p0 in the success–failure condition (np0 ≥ 10 and n(1 − p0) ≥ 10) and ensure independence/random sampling. For a quick refresher, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and any practice problems at (https://library.fiveable.me/practice/ap-statistics).
How do I tell if my sample was collected randomly enough to meet the independence condition?
Check two things. 1) Was the data collected by a random method? The CED says you need a random sample or a randomized experiment. So look for wording like “random sample,” “simple random sample,” or a described random procedure (random-digit dialing, random selection from a roster, random assignment in an experiment). If you see convenience sampling, voluntary response, or only certain clusters chosen without randomization, independence isn’t met. 2) If sampling without replacement, use the 10% condition: n ≤ 0.10 · N (sample ≤ 10% of the population). If that holds, you can treat sampled units as approximately independent. If the problem explicitly says “random sample” on the exam, you can state that and check the 10% rule. If it doesn’t, justify why the method is or isn’t random. Reminder: for a one-sample z-test for a proportion you also must check the success–failure condition (np0 ≥ 10 and n(1−p0) ≥ 10) separately. For more help, see the Topic 6.4 study guide (https://library.fiveable.me/ap-statistics/unit-6/setting-up-test-for-population-proportion/study-guide/QLu7hUN0rwtnxLF7YdBT) and practice questions (https://library.fiveable.me/practice/ap-statistics).