How to Tell if a Sample is Unbiased
An unbiased estimator is one that produces estimates that are on average as close as possible to the true population parameter. This means that if you repeatedly draw samples from the population and use the estimator to make inferences about the population parameter, the average of those estimates will be equal to the true population parameter. ⚖️
For example, if you wanted to estimate the mean height of all the students in your school, you could take a sample of students and measure their heights. If the mean height of the sample (the sample statistic) is equal to the mean height of the entire school (the population parameter), then your estimator is unbiased. On the other hand, if the sample mean consistently underestimates or overestimates the true mean height of the school, then your estimator is biased.
A sample is unbiased if the estimator value (sample statistic) is equal to the population parameter. For example, if the sampling distribution mean (x̅) is equal to the population mean (𝝁) or if the average of our sample proportions (p) is equal to our population proportion (𝝆), then our sample is unbiased!

How to Tell if a Sample has Minimum Variability
A sampling distribution has a minimum amount of variability (spread) if all samples have statistics that are approximately equivalent to one another.
It is impossible to have no variability, due to the nature of random sampling. This is because the sample you are using to make the inference is only a small subset of the entire population, and so it is subject to sampling error. Therefore, there will always be some level of uncertainty or variability in the estimate when you use an estimator to make inferences about a population parameter.
However, a larger sample size will minimize variability in a sampling distribution!
Bias and Variability
A Recap on Skewness
Skewness is a measure of the symmetry of a distribution. A distribution is symmetric if it is roughly the same on both sides of the center, like a bell curve. A distribution is skewed if it is not symmetric, with more of the values clustered on one side or the other. For example, if a distribution is skewed to the left, it means that there are more values on the right side of the distribution and fewer values on the left side.
If a sample is equally spread out around the mean, it is not necessarily unbiased, but it is less likely to be biased than a sample that is heavily skewed in one direction or the other. However, other factors can also contribute to bias, such as sampling methods or the way that the sample was collected.
Bias relates to how skewed (also how screwed) the distribution is. Specifically, if an entire distribution is on the left side of our population parameter, it is skewed to the left. If a sample is equally spread out around the mean, then there is no bias.
The more spread out a distribution is, the more variability it has. The standard deviation of the sampling distribution is the estimator of the population standard deviation. If the standard deviation of the sampling distribution is equal to population standard deviation, it is said that the standard deviation of sampling distribution is the consistent estimator. High variability can be fixed by increasing your sample size, but if your sample does have high bias, there is no statistical way to fix it.
A good illustration for bias and variability is a bullseye. Bias measures how precise the archer is (how close to the bullseye), while variability measures how consistent he/she is. See the illustrations below for different circumstances regarding bias and variability:
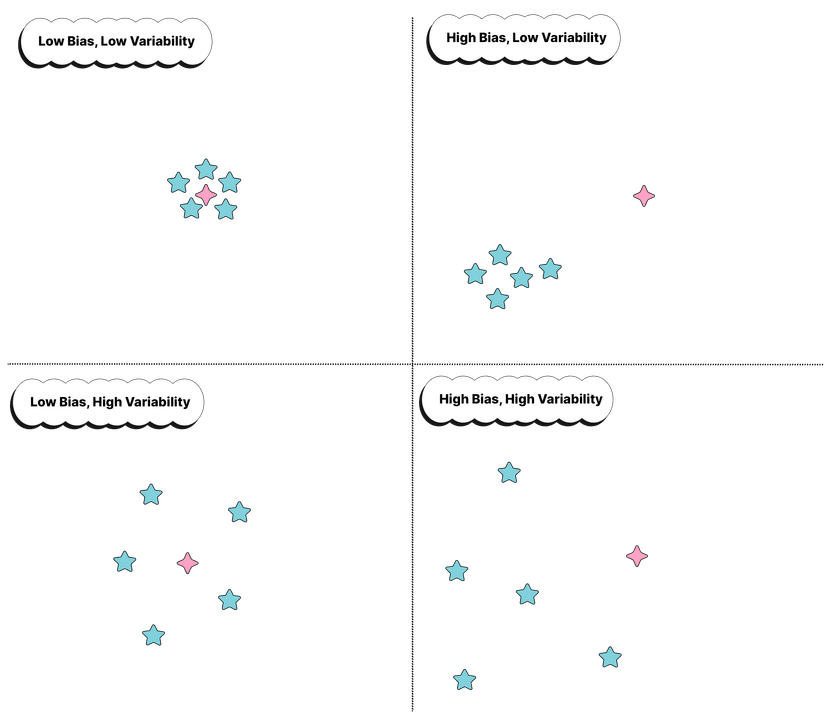
In this analogy, the bullseye represents the true population parameter, and the archer's shots represent the estimates produced by the estimator.
If the archer is very accurate but not very consistent, their shots will be close to the bullseye but may be scattered around it. This would correspond to a situation where the estimator has high variability but low bias.
On the other hand, if the archer is very consistent but not very accurate, their shots will all be close to each other but may be far from the bullseye. This would correspond to a situation where the estimator has high bias but low variability.
A good estimator should aim for both low bias and low variability, producing estimates that are both accurate and consistent.
Practice Problem
Suppose that you are asked to estimate the mean income of all the households in your town. You decide to use a sample of 100 households, selected using a random sampling method. After collecting the data, you calculate the sample mean income to be $$50,000.
a) Explain whether or not this sample is biased, and give a reason for your answer.
b) Explain whether or not the sample mean income is an unbiased estimator of the population mean income, and give a reason for your answer.
c) Suppose that you later learn that the true population mean income is actually $$55,000. Explain how this information affects your conclusions about the bias of the sample and the estimator in parts (a) and (b).
d) Discuss one potential source of bias that could have affected the results of this study, and explain how it could have influenced the estimate of the population mean income. (Note how this connects to Unit 3: Collecting Data)
Answer
a) Since the sample of 100 households was selected using a random sampling method (i.e., SRS, stratified or cluster sampling), the sample is not biased as it is representative of the entire population and its characteristics.
b) The sample mean income is an unbiased estimator of the population mean income if the sample was selected randomly and is representative of the entire population. If the sample meets these conditions, then the sample mean should be an unbiased estimate of the population mean, on average. Again, since we used a random sampling method, the sample mean income is indeed an unbiased estimator.
c) If the true population mean income is actually 50,000 is an underestimate of the population mean. This means that the sample is biased, because it consistently produces estimates that are too low. It also suggests that the sample mean is a biased estimator, because it systematically produces estimates that are too low.
d) One potential source of bias in this study could be nonresponse bias, which occurs when certain groups of individuals are more or less likely to respond to the survey. For example, if households with higher incomes are more likely to respond to the survey, the sample could be biased toward higher incomes and produce an overestimate of the population mean. On the other hand, if households with lower incomes are more likely to respond, the sample could be biased toward lower incomes and produce an underestimate of the population mean.
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| biased | A property of an estimator where the average value of the estimator does not equal the population parameter being estimated. |
| estimator | A statistic used to estimate or approximate the value of a population parameter based on sample data. |
| population parameter | A numerical characteristic of an entire population, such as the mean, proportion, or standard deviation. |
| sample statistic | A numerical value calculated from sample data that is used to estimate the corresponding population parameter. |
| unbiased | A property of an estimator where the average value of the estimator equals the population parameter being estimated. |
| variability | The spread or dispersion of data values in a distribution. |
Frequently Asked Questions
How do I know if an estimator is biased or unbiased?
An estimator is unbiased if the long-run average of that estimator equals the true population parameter—i.e., the estimator’s expected value equals the parameter. Practically: look at the sampling distribution of the estimator. If μ_est = E(estimator) = parameter, it’s unbiased; if not, it’s biased (estimation bias = E(estimator) − parameter). Examples you should memorize: the sample mean x̄ is an unbiased estimator of μ (E[x̄]=μ); the sample proportion p̂ is unbiased for p (E[p̂]=p). Check bias by calculating E(estimator) (or reasoning from known sampling distributions) and compare to the parameter. Also keep variability in mind: unbiased doesn’t mean low variance—use standard error and mean squared error to judge overall accuracy. This is exactly what the CED emphasizes for Topic 5.4 (UNC-3.I.1). For a quick refresher, see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the formula for calculating a point estimate?
A point estimate is just a sample statistic used to estimate a population parameter. The “formula” depends on the parameter you want: - Population mean μ → point estimate: sample mean x̄ = (Σ xi)/n. - Population proportion p → point estimate: p̂ = x/n (x = count of successes). - Population variance σ² → common point estimate: sample variance s² = Σ(xi − x̄)²/(n − 1). An estimator is unbiased if its expected value equals the population parameter (E[x̄] = μ, E[p̂] = p). On the AP exam you’ll use these statistics and their standard errors (e.g., SE(x̄) = s/√n, SE(p̂) = √[p̂(1−p̂)/n]) when doing sampling-distribution / inference problems (formulas appear on the AP formula sheet). For a quick review of biased vs. unbiased point estimates, see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF). More unit review (https://library.fiveable.me/ap-statistics/unit-5) and practice problems (https://library.fiveable.me/practice/ap-statistics) are available if you want extra practice.
When do I use sample mean vs sample proportion as an estimator?
Use the sample mean (x̄) when the population parameter you want is a population mean (μ)—that is, your data are quantitative (heights, times, scores). Use the sample proportion (p̂) when the parameter is a population proportion (p)—your data are categorical with “success/failure” (yes/no). Each sample statistic is a point estimator for its corresponding parameter (CED UNC-3.J.2). Both estimators can be unbiased: E(x̄)=μ and E(p̂)=p, so on average they hit the true parameter (UNC-3.I.1). Check conditions for modeling their sampling distributions: for x̄ use CLT or normal population (σ/√n or s/√n), for p̂ use binomial-based normal approx when np and n(1−p) are large enough (see Topic 5.3 and 5.5). Standard error tells you estimator variability and is needed for CIs/tests—these formulas are on the AP formula sheet. For quick review, see the Fiveable Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice questions (https://library.fiveable.me/practice/ap-statistics).
What's the difference between a biased and unbiased estimator?
A quick way to tell them apart: an estimator is unbiased if the long-run average of that statistic equals the true population parameter. Formally, E(estimator) = parameter. Biased means E(estimator) ≠ parameter—it systematically over- or underestimates. Examples: the sample mean x̄ is an unbiased estimator of the population mean μ, so the sampling distribution of x̄ has center μ (and spread σ/√n). The sample variance using n−1 (s^2) is unbiased for σ^2, while the version dividing by n is biased. Bias is about center (expected value); variability (standard error) is a separate issue—an estimator can be unbiased but very variable. MSE (mean squared error) combines bias and variance if you need a single accuracy measure. Law of large numbers tells you consistent, unbiased estimators tend to get close to the true value as n grows. For AP review, see Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and grab practice problems at (https://library.fiveable.me/practice/ap-statistics).
I don't understand why some estimators are unbiased - can someone explain this?
An estimator is unbiased when its long-run average (its expected value) equals the true population parameter. In other words, if you repeated the same random sampling process many times and calculated the estimator each time, the mean of those estimates would hit the real value. Formally: E(estimator) = parameter (that's UNC-3.I in the CED). Why that matters: unbiasedness is a property of the estimator’s sampling distribution—it tells you there’s no systematic error (no consistent over- or under-estimating). It doesn’t mean any one sample gives the true value (estimators still have variability, measured by standard error). So unbiased + small standard error is ideal. The law of large numbers and CLT help: with larger n the sampling distribution tightens (less variability) so unbiased estimators tend to give estimates closer to the true parameter more often. For a quick topic review, see the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF). For extra practice problems, check the AP practice bank (https://library.fiveable.me/practice/ap-statistics).
How do I calculate the expected value of an estimator to check if it's unbiased?
To check unbiasedness, compute the estimator’s expected value and compare it to the population parameter. Formally: - If T is your estimator (a statistic), E(T) = Σ t · P(T = t) for discrete cases, or the integral for continuous cases. - More usefully, use linearity of expectation: if T is a function of sample observations, take the expectation of that function. If E(T) = parameter, T is unbiased; if not, it’s biased (bias = E(T) − parameter). Quick AP examples you should know: - Sample mean: E(X̄) = μ → X̄ is unbiased for μ. - Sample proportion: E(p̂) = p → p̂ is unbiased for p. On the exam you’ll often argue unbiasedness by writing E(T) and using known facts (linearity, independence). For sampling-distribution intuition and examples, see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
Is the sample standard deviation biased or unbiased and why?
Short answer: the usual sample standard deviation s = sqrt( (1/(n-1)) Σ(xi − x̄)² ) is a biased estimator of the population standard deviation σ. Why: an estimator is unbiased when its expected value equals the population parameter (CED UNC-3.I.1). The sample variance s² with denominator (n−1) is unbiased: E[s²] = σ². But taking the square root is a nonlinear transformation, so E[s] ≠ σ (in fact E[s] is usually a bit smaller than σ). The bias shrinks as n grows, and s is consistent (by the law of large numbers s → σ). For AP-style answers, name the estimator, state the expected-value definition of unbiasedness, give E[s²]=σ² and note E[s]≠σ. For a refresher, see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice problems (https://library.fiveable.me/practice/ap-statistics).
What does it mean when they say an estimator is unbiased "on average"?
“Says an estimator is unbiased ‘on average’” means: if you could take many random samples from the same population and compute the estimator each time, the average of all those estimates (the expected value of the estimator) would equal the true population parameter. In AP language: an estimator (a sample statistic used as a point estimator) is unbiased when E(estimator) = parameter (CED UNC-3.I.1). That doesn’t guarantee every single sample gives the true value—individual estimates still vary (standard error). Unbiased means no systematic over- or under-estimation in the long run; repeated sampling centers the sampling distribution at the true parameter. The Law of Large Numbers and sampling-distribution ideas in Unit 5 explain why repeated-sample averages converge to the parameter. For more AP-aligned review see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
How do I solve problems where I need to find if an estimator is unbiased?
To check if an estimator is unbiased, compute its expected value (using the sampling distribution) and see whether E(estimator) = the population parameter. If equal, it’s unbiased; if not, the difference is the estimator’s bias. Steps you can follow: - Write the estimator algebraically (e.g., \bar{X} = (1/n)Σ Xi, or \hat p = X/n). - Use linearity of expectation and known expectations of the Xi (E(Xi)=μ, E(indicator)=p) to find E(estimator). - Compare to the parameter. Bias = E(estimator) − parameter. Quick examples: - \bar{X} is unbiased for μ because E(\bar{X}) = (1/n)ΣE(Xi)=μ. - \hat p is unbiased for p because E(X)/n = np/n = p. - The sample variance with 1/(n−1) (s^2) is unbiased for σ^2; using 1/n gives a biased estimator. AP tip: be ready to “explain why” by showing the expected-value calculation (UNC-3.I). For more practice and explanations, see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and try problems at (https://library.fiveable.me/practice/ap-statistics).
When estimating population parameters, which sample statistics should I use?
Use the sample statistic that matches the parameter you want—those sample statistics are your point estimators. Key ones to memorize for AP Stats (Topic 5.4): - Population mean μ → sample mean x̄. x̄ is an unbiased estimator: E(x̄)=μ. Its standard error ≈ s/√n (use σ/√n only if σ is known). - Population proportion p → sample proportion p̂. p̂ is unbiased: E(p̂)=p. Its SE = √[p̂(1−p̂)/n]. - Population variance σ² → sample variance s² (use the n−1 denominator); s² is an unbiased estimator of σ². Why this matters: “unbiased” means the estimator’s expected value equals the true parameter (CED UNC-3.I). Every estimator has variability (standard error) you must estimate and can model with a sampling distribution (CLT and Law of Large Numbers make x̄ and p̂ behave well as n grows). AP exam expects you to identify these estimators, their SE formulas (see the formula sheet) and to explain unbiasedness—review Fiveable’s Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice problems (https://library.fiveable.me/practice/ap-statistics).
I'm confused about point estimates vs interval estimates - what's the difference?
A point estimate is a single-number guess for a population parameter—for example, the sample mean x̄ or sample proportion p̂. In AP terms, a sample statistic is a point estimator (UNC-3.J.2). Whether that estimator is good depends on its sampling distribution: an estimator is unbiased if its expected value equals the true parameter (UNC-3.I.1). An interval estimate (confidence interval) gives a range of plausible values plus a confidence level (e.g., 95%) and incorporates the estimator’s variability via the standard error. So a point estimate gives one best guess; an interval estimate gives that guess ± margin of error and communicates uncertainty. On the exam you may be asked to “Give a point estimate or interval estimate”—know both when each is appropriate. Review Topic 5.4 (biased vs unbiased point estimates) on Fiveable (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice more at (https://library.fiveable.me/practice/ap-statistics).
Why is s² unbiased but s is biased when estimating population variance?
An estimator is unbiased if its expected value equals the population parameter. For variance, the sample variance s² = (1/(n−1)) Σ(xi − x̄)² is unbiased because E[Σ(xi − x̄)²] = (n−1)σ², so dividing by (n−1) gives E[s²] = σ². The (n−1) corrects for the fact we used the sample mean x̄ (a random quantity) instead of the true mean μ—using 1/n would systematically underestimate variance. The sample standard deviation s = sqrt(s²) is biased because the square root is a nonlinear transformation. E[s] ≠ sqrt(E[s²]) in general, so even though s² centers on σ², taking the square root pulls the expectation away from σ (for typical sample sizes E[s] < σ). This bias shrinks as n grows; by the law of large numbers both s and s² are consistent (they converge to the true parameter). For the AP exam you should explain unbiasedness in terms of expected value and show the algebraic reason for s² (see the Topic 5.4 study guide for a refresher: https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF). For extra practice, try problems at (https://library.fiveable.me/practice/ap-statistics).
How do I calculate point estimates for word problems about populations?
A point estimate is just the sample statistic you use to estimate a population parameter. Steps for word problems: 1. Identify the population parameter (mean μ or proportion p). 2. Pick the corresponding estimator: sample mean x̄ for μ or sample proportion p̂ = x/n for p. (For other parameters you might use sample variance or regression slope.) 3. Calculate the statistic from the data: x̄ = (Σxi)/n, p̂ = x/n. That number is your point estimate. 4. Note bias: an estimator is unbiased if its expected value equals the true parameter (e.g., E(x̄)=μ and E(p̂)=p). If a problem asks about bias, state the expected value and compare. 5. Report precision: give the standard error—s/√n for x̄ (or σ/√n if σ known) and √[p̂(1−p̂)/n] for p̂—and mention CLT/Law of Large Numbers when justifying sampling behavior. These are the AP ideas in Topic 5.4 (point estimator, unbiased estimator, standard error). For a focused review see the Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF), the Unit 5 overview (https://library.fiveable.me/ap-statistics/unit-5), and practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the variability of an estimator and how do I find it?
Variability of an estimator = how much the estimator (like \(\bar{x}\) or \(\hat{p}\)) would change from sample to sample. It’s quantified by the variance or standard error of the estimator—think of standard error (SE) as the estimator’s SD. You find it from the sampling distribution: - For a sample mean: Var(\(\bar{X}\)) = \(\sigma^2/n\), so SE = \(\sigma/\sqrt{n}\). If σ unknown use SE ≈ \(s/\sqrt{n}\). - For a sample proportion: Var(\(\hat{p}\)) = \(p(1-p)/n\), SE = \(\sqrt{p(1-p)/n}\); in practice use \(\hat{p}\) inside the formula. - For differences or regression slopes, use the corresponding SE formulas (see AP formula sheet). Lower SE → less variability → more precise, and as n grows SE shrinks (law of large numbers/CLT). These ideas are part of Topic 5.4 on the CED (sampling distributions, unbiasedness, standard error). Review the topic guide on Fiveable (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice problems (https://library.fiveable.me/practice/ap-statistics) to get quick examples.
Can someone explain step by step how to determine if a sample statistic is an unbiased estimator?
Step-by-step: how to check if a sample statistic is an unbiased estimator 1) Name the estimator and the true parameter (e.g., sample mean x̄ for population mean μ, sample proportion p̂ for population proportion p). 2) Find the sampling distribution or compute the estimator’s expected value E(estimator). For many common estimators this is known: E(x̄)=μ, E(p̂)=p. 3) Compare E(estimator) to the parameter. If E(estimator) = parameter for all possible samples (or all values of the parameter), the estimator is unbiased. If not, it’s biased and the bias = E(estimator) − parameter. 4) If an analytic derivation is hard, approximate E(estimator) by simulation: draw many random samples, compute the statistic each time, and take the average—if that average ≈ the true parameter, it’s effectively unbiased. 5) Remember AP CED point: unbiased means “on average equal to the population parameter” (UNC-3.I.1). Also note variance/standard error measure variability (so unbiased doesn’t mean low variability). Examples: x̄ unbiased for μ; p̂ unbiased for p; s² with denominator (n−1) is unbiased for σ². For more review see the AP Topic 5.4 study guide (https://library.fiveable.me/ap-statistics/unit-5/biased-unbiased-point-estimates/study-guide/eZ5sR9XOkLB1o9KKpMHF) and practice problems (https://library.fiveable.me/practice/ap-statistics).