4.9 Combining Random Variables

Combining random variables means finding the mean and standard deviation when you add, subtract, scale, or shift random variables. Means always add or subtract directly, but standard deviations never add.

Combining Random Variables

In AP Statistics, combining random variables means finding the mean and standard deviation of a sum, difference, or linear combination. Means add and subtract directly, but standard deviations do not. For independent random variables, combine variances first, then take the square root.

A good exam rule is: center follows the operation, spread follows variance. If you add or subtract independent random variables, add their variances either way. If you multiply a random variable by a constant, multiply the standard deviation by the absolute value of that constant.

more resources to help you study

practice multiple choiceFRQ practice & scoringcheatsheetsscore calculatorkey terms

Why This Matters for the AP Statistics Exam

This topic in AP Statistics gives you the tools to predict the center and spread of a combined or transformed random variable. You will use these ideas when you work with sums and differences of random variables, and they set up the formulas behind sampling distributions later in the course. On both multiple-choice and free-response questions, you may need to calculate a combined mean or standard deviation, show the structure of your formula, and interpret the result with correct units.

Key Takeaways

• For real numbers $a$ and $b$, the mean of $aX + bY$ is $a\mu_X + b\mu_Y$, whether or not the variables are independent.
• For a linear transformation $Y = a + bX$, the mean is $\mu_Y = a + b\mu_X$ and the standard deviation is $\sigma_Y = |b|\sigma_X$.
• Adding a constant shifts the mean but does not change the standard deviation or the shape.
• Multiplying by a constant changes both the mean and the standard deviation, but not the shape.
• For independent $X$ and $Y$, the variance of $aX + bY$ is $a^2\sigma_X^2 + b^2\sigma_Y^2$.
• Variances add for both sums and differences of independent variables. Standard deviations do not add, so always work with variance first.

Linear Transformations of a Random Variable

Transforming a random variable means adding or subtracting a constant, or multiplying or dividing by a constant. This can simplify calculations or change units to something easier to interpret.

When you add or subtract a constant $a$, you shift every value by the same amount. The center moves, but the spread and shape stay the same.

$\mu_Y = a + \mu_X$ $\sigma_Y = \sigma_X$

When you multiply by a constant $b$, you stretch or shrink the values. Both the center and the spread change, but the shape does not.

For the general linear transformation $Y = a + bX$:

$\mu_Y = a + b\mu_X$ $\sigma_Y = |b|\sigma_X$

The absolute value matters because standard deviation is never negative. If $a > 0$ and $b > 0$, the transformed distribution has the same shape as the original.

Quick summary of effects:

• Adding or subtracting a constant: changes center and location, not variability or shape.
• Multiplying or dividing by a constant: changes center, location, and variability, not shape.

Combining Two Random Variables

You can also combine two random variables into a new one. The rule for the mean is simple, but the rule for spread takes more care.

Mean of a Sum or Difference

For any two random variables $X$ and $Y$:

Sum: If $S = X + Y$, then $\mu_S = \mu_X + \mu_Y$.

Difference: If $D = X - Y$, then $\mu_D = \mu_X - \mu_Y$. The order of subtraction matters here.

More generally, the mean of $aX + bY$ is $a\mu_X + b\mu_Y$. This holds whether or not the variables are independent.

Independent random variables: Two random variables are independent if knowing the value of one does not change the probability distribution of the other.

Standard Deviation of a Sum or Difference

Standard deviations do not add. For independent variables, you add the variances and then take the square root.

Sum: For independent $X$ and $Y$, if $S = X + Y$:

$\sigma_S^2 = \sigma_X^2 + \sigma_Y^2 \qquad \sigma_S = \sqrt{\sigma_X^2 + \sigma_Y^2}$

Difference: For independent $X$ and $Y$, if $D = X - Y$:

$\sigma_D^2 = \sigma_X^2 + \sigma_Y^2 \qquad \sigma_D = \sqrt{\sigma_X^2 + \sigma_Y^2}$

Notice that you add the variances for a difference, just like a sum. You never subtract variances. For the general case $aX + bY$ with independent variables, the variance is $a^2\sigma_X^2 + b^2\sigma_Y^2$.

How to Use This on the AP Statistics Exam

Problem Solving

• Start by identifying whether you are transforming one variable or combining two.
• For means, apply $a\mu_X + b\mu_Y$ directly.
• For standard deviations, switch to variance first. Square each standard deviation, combine with the correct coefficients, then take the square root.
• Check that you used $|b|$ when scaling a single variable.
• Confirm the variables are independent before using the variance addition rule.

Free Response

• Write the formula with values substituted in, not just the final number. Showing the structure of the multiplication and addition communicates your reasoning clearly.
• Keep units attached to your mean and standard deviation.
• Interpret the result in context. For a study-hours problem, the mean is the expected total hours and the standard deviation describes how much that total varies.

Common Trap

• Adding standard deviations instead of variances is the most frequent error. Always go through variance.

Practice Problem

Two random variables, X and Y, represent the number of hours a student spends studying for a math test and the number of hours a student spends studying for a science test, respectively. The probability distributions of X and Y are shown in the tables below:

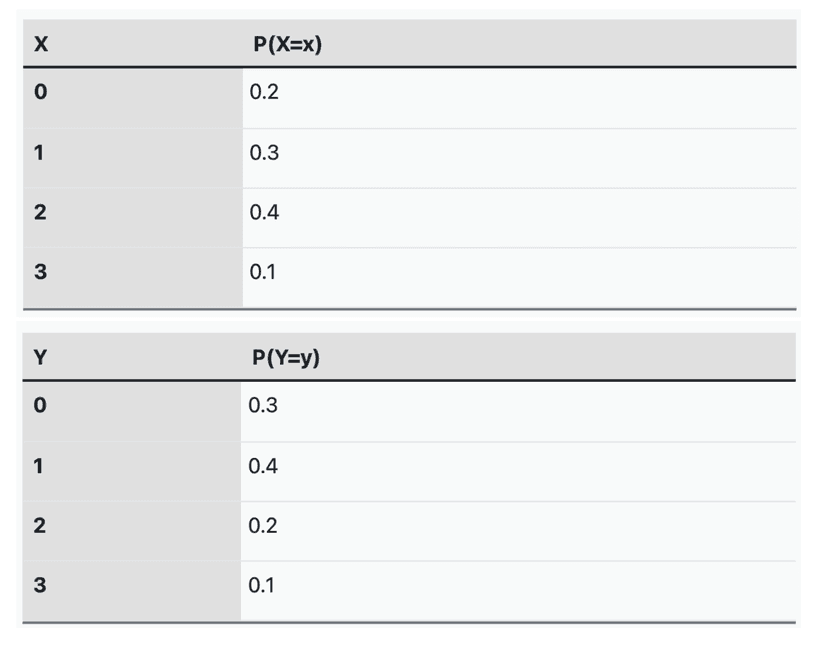
A new random variable, Z, represents the total number of hours a student spends studying for both tests.

(a) Calculate the mean or expected value of Z.

(b) Calculate the standard deviation of Z.

(c) Interpret the results in the context of the problem.

For part (a), use $\mu_Z = \mu_X + \mu_Y$. For part (b), assuming X and Y are independent, use $\sigma_Z = \sqrt{\sigma_X^2 + \sigma_Y^2}$. For part (c), describe the expected total study time and how much that total tends to vary, in hours.

Common Misconceptions

• Standard deviations add for sums. They do not. Variances add for independent variables, and you take the square root at the end.
• You subtract variances for a difference. You still add the variances. Subtraction applies only to the means.
• Adding a constant changes the spread. Shifting every value by the same amount moves the center but leaves the standard deviation unchanged.
• Scaling does not affect the standard deviation. Multiplying by a constant $b$ multiplies the standard deviation by $|b|$, even though it leaves the shape the same.
• The variance rules always apply. The simple variance addition formula requires independent variables. If the variables are not independent, that formula does not hold.
• Order does not matter for a difference of means. $X - Y$ and $Y - X$ give opposite signs, so the order of subtraction matters for the mean.

Related AP Statistics Guides

• Unit 4 Overview: Probability, Random Variables, and Probability Distributions
• 4.1 Introducing Statistics: Random and Non-Random Patterns?
• 4.2 Estimating Probabilities Using Simulation
• 4.3 Introduction to Probability
• 4.4 Mutually Exclusive Events
• 4.7 Introduction to Random Variables and Probability Distributions