The least squares regression line (LSRL) is the best linear regression line that exists in the sense that it minimizes the sum of the squared residuals. (Remember from previous sections that residuals are the differences between the observed values of the response variable, y, and the predicted values, ŷ, from the model.)
The least squares criterion is used to find the line of best fit because it minimizes the sum of the squared residuals. This is done by minimizing the difference between the observed and predicted values, which in turn maximizes the accuracy of the model.
The least squares regression line is given by the formula ŷ = a + bx, where ŷ is the predicted value of the response variable, x is the predictor or explanatory variable, a is the y-intercept (the value of ŷ when x is zero), and b is the slope (the change in ŷ per unit change in x). The y-intercept and slope can be calculated using the one-variable statistics of x and y.
The reason why the residuals are squared in the least squares criterion is to give more weight to larger residuals and to eliminate the cancellation of positive and negative residuals. Squaring the residuals also has the effect of penalizing larger deviations from the line of best fit more heavily, which can help to reduce the overall variance in the model.
LSRL—Slope
The slope is the predicted increase in the response variable with an increase of one unit of the explanatory variable. To find the slope, we have the formula:
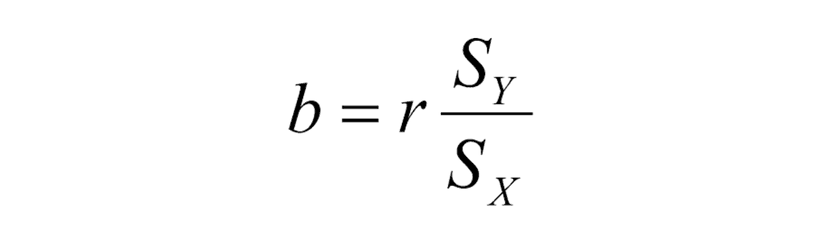
(where b is the slope, r is the correlation coefficient between x and y, sy is the standard deviation of y, and sx is the standard deviation of x.)
The least squares estimate of the slope takes into account the variability in both x and y and the strength of the linear relationship between them. It is a weighted average of the deviation of y from the mean of y over the deviation of x from the mean of x, with the correlation coefficient, r, serving as a correction factor.

Template for Interpretation
When asked to interpret the slope of an LSRL, follow the template below:
"There is a predicted increase/decrease of ______ (slope in units of y variable) for every 1 (unit of x variable)."
Big Three
LSRL—y-intercept
Once you have calculated the slope of the least squares regression line, you can use the point-slope form to find the y-intercept and the general formula for the line.
The point-slope form of a linear equation is given by:
ŷ - y1 = m(x - x1)
where ŷ is the predicted value of the response variable, m is the slope of the line, x is the predictor or explanatory variable, and (x1, y1) is a point on the line.
The LSRL always passes through the point (x̄, ȳ), where x̄ is the mean of the predictor variable and ȳ is the mean of the response variable. Therefore, we can use this point to find the y-intercept of the line using the point-slope form.
Substituting the values into the point-slope form, we have:
ŷ - ȳ = b(x - x̄)
Solving for ŷ, we get:
ŷ = bx + (-bx̄ + ȳ)
The expression in parentheses is the y-intercept of the line, which represents the value of the response variable when the explanatory variable is zero.
Template for Interpretation
Template time! When asked to interpret a y-intercept of an LSRL, follow the template below:
"The predicted value of (y in context) is _____ when (x value in context) is 0 (units in context)."
Big Three
LSRL—Coefficient of Determination
The coefficient of determination, also known as R-squared, is a statistic that is used to evaluate the fit of a linear regression model (how well the LSRL fits the data). It is a measure of how much of the variability in the response variable (y) can be explained by the model.
R-squared can be defined as the square of the correlation coefficient (r) between the observed and predicted values of the response variable. It is represented by the symbol R-squared and ranges from 0 to 1, with a value of 0 indicating no relationship between the explanatory and response variables (LSRL does not model the data at all) and a value of 1 indicating a perfect linear relationship.
There is also another formula for r^2 as well. This formula is:

This is saying that this is the percent difference between the variance of y and the sum of the residual squared. In other words, this is the reduction in the variation of y due to the LSRL. When interpreting this we say that it is the “percentage of the variation of y that can be explained by a linear model with respect to x.”
%5E2%7D%7Bs_y%5E2%7D#0)Template for Interpretation
Template time yet again! When asked to interpret a coefficient of determination for a least squares regression model, use the template below:
"____% of the variation in (y in context) is due to its linear relationship with (x in context)."
Big Three
LSRL—Standard Deviation of the Residuals
The last statistic we will talk about is the standard deviation of the residuals, also called s. S is the typical residual by a given data point of the data with respect to the LSRL. The formula for s is given as:
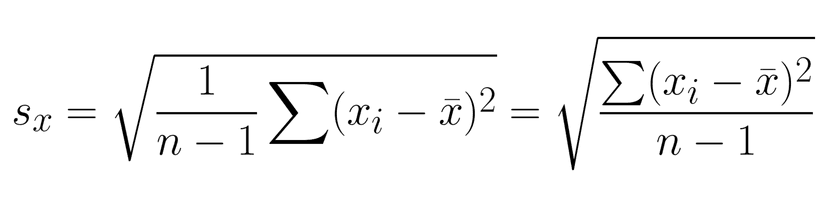
which looks similar to the sample standard deviation, except we will divide by n-2 and not n-1. Why? We will learn more about s when we learn inference for regression in Unit 9.
Reading a Computer Printout
On the AP test, it is very likely that you will be expected to read a computer printout of the data. Here is a sample printout with a look at where most of the statistics you will need to use are (the rest you will learn in Unit 9):
Courtesy of Starnes, Daren S. and Tabor, Josh. The Practice of Statistics—For the AP Exam, 5th Edition. Cengage Publishing.Always use R-Sq, NEVER R-Sq(adj)!
🎥 Watch: AP Stats - Least Squares Regression Lines
Practice Problem
A researcher is studying the relationship between the amount of sleep (in hours) and the performance on a cognitive test. She collects data from 50 participants and fits a linear regression model to the data. The summary of the model is shown below:
Summary of Linear Regression Model:
Response variable: Performance on cognitive test (y)
Explanatory variable: Amount of sleep (x)
Slope (b): -2.5
Y-intercept (a): 50
Correlation coefficient (r): -0.7
R-squared: 0.49
a) Interpret the slope of the model in the context of the problem.
b) Interpret the y-intercept of the model in the context of the problem.
c) Interpret the correlation coefficient of the model in the context of the problem.
d) Interpret the R-squared value of the model in the context of the problem.
e) Based on the summary of the model, do you think that the amount of sleep has a significant effect on the performance on the cognitive test? Why or why not?
f) Suppose the researcher collects data from an additional 50 participants and fits a new linear regression model to the combined data. The summary of the new model is shown below:
Slope (b): -1.9
Y-intercept (a): 48
Correlation coefficient (r): -0.6
R-squared: 0.36
Compare the two models and explain how the new model differs from the original model in terms of the strength and direction of the relationship between the amount of sleep and the performance on the cognitive test.
Answers
a) The slope of the model is -2.5, which means that for every one-hour increase in the amount of sleep, the performance on the cognitive test is predicted to decrease by 2.5 points.
b) The y-intercept of the model is 50, which means that the performance on the cognitive test is predicted to be 50 points when the amount of sleep is zero.
c) The correlation coefficient of the model is -0.7, which indicates a strong negative linear relationship between the amount of sleep and the performance on the cognitive test. A negative correlation means that as the amount of sleep increases, the performance on the cognitive test decreases.
d) The R-squared value of the model is 0.49, which means that 49% of the variability in the performance on the cognitive test can be explained by the model. This indicates that the model is able to capture a significant portion of the variance in the data, but there may be other factors that are not being considered that are also contributing to the performance on the cognitive test.
e) Based on the summary of the model, it appears that the amount of sleep has a significant effect on the performance on the cognitive test. The slope of the model is negative, indicating a negative relationship between the variables, and the correlation coefficient is strong (close to -1). However, it is important to note that the R-squared value is not 1, which means that there are other factors that are also influencing the performance on the cognitive test.
f) In the new model, the slope is -1.9, which is slightly less negative than the slope in the original model (-2.5). This suggests that the relationship between the amount of sleep and the performance on the cognitive test is slightly weaker in the new model compared to the original model.
- The y-intercept is also slightly lower in the new model (48) compared to the original model (50).
- The correlation coefficient is slightly weaker in the new model (-0.6) compared to the original model (-0.7).
- Finally, the R-squared value is lower in the new model (0.36) compared to the original model (0.49).
Overall, these differences suggest that the new model has a slightly weaker and less negative relationship between the amount of sleep and the performance on the cognitive test compared to the original model.
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| coefficient of determination | The value r², which represents the proportion of variation in the response variable that is explained by the explanatory variable in the regression model. |
| coefficients | The numerical values in a regression equation that represent the slope and y-intercept of the least-squares regression line. |
| correlation | A numerical measure (r) that describes the strength and direction of a linear relationship between two variables, ranging from -1 to 1. |
| explanatory variable | A variable whose values are used to explain or predict corresponding values for the response variable. |
| least-squares regression line | A linear model that minimizes the sum of squared residuals to find the best-fitting line through a set of data points. |
| parameter | A numerical summary that describes a characteristic of an entire population. |
| predicted value | The estimated response value obtained from a regression model, denoted as ŷ. |
| residual | The difference between the actual observed value and the predicted value in a regression model, calculated as residual = y - ŷ. |
| response variable | A variable whose values are being explained or predicted based on the explanatory variable. |
| sample standard deviation | The standard deviation calculated for a sample, denoted by s, using the formula s = √(1/(n-1) ∑(xᵢ-x̄)²). |
| simple linear regression | A regression model that describes the linear relationship between one explanatory variable and one response variable. |
| slope | The value b in the regression equation ŷ = a + bx, representing the rate of change in the predicted response for each unit increase in the explanatory variable. |
| y-intercept | The value a in the regression equation ŷ = a + bx, representing the predicted response value when the explanatory variable equals zero. |
Frequently Asked Questions
How do I find the formula for a least squares regression line?
The least-squares regression line (predicted y = a + b x) is the line that minimizes the sum of squared residuals and always passes through the mean point (x̄, ȳ). On the AP, compute the slope b and intercept a with these formulas from the CED: b = r · (s_y / s_x) and a = ȳ − b·x̄. So your prediction rule is ŷ = a + b x. Interpretations: b is the change in predicted y for a one-unit increase in x; a is the predicted y when x = 0 (may be meaningless in context). Also remember r² = (correlation)² gives the proportion of y’s variation explained by x. Check residuals (no clear pattern) and avoid extrapolation beyond your x-values. Formulas are on the AP formula sheet and your calculator does this quickly—practice with the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj), Unit 2 overview (https://library.fiveable.me/ap-statistics/unit-2), and lots of practice problems (https://library.fiveable.me/practice/ap-statistics).
What's the difference between correlation and the coefficient of determination?
Correlation (r) and the coefficient of determination (r²) are related but mean different things: - Correlation r: a number between −1 and 1 that measures the strength and direction of a linear relationship between two quantitative variables. Sign matters (positive/negative), magnitude tells you how close points are to a straight line. It’s used in the slope formula b = r(s_y/s_x) (CED DAT-1.G.2). - Coefficient of determination r²: the square of r (ranges 0 to 1). It has no sign and tells you the proportion of variation in the response variable y that’s explained by the explanatory variable x in the least-squares regression model (CED DAT-1.G.4). Example: r = 0.80 → r² = 0.64 means 64% of y’s variability is explained by x; 36% is unexplained. On the AP exam you’ll report r for association and r² when interpreting how much variation the LSRL explains. For a quick review, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
I'm confused about what r squared actually means - can someone explain it simply?
r² (the coefficient of determination) tells you how much of the variation in the response variable y is explained by the explanatory variable x in your least-squares line. In simple linear regression r² = r² (the square of the correlation). If r² = 0.64, for example, 64% of the variability in y is explained by the linear model and 36% is unexplained (left in the residuals). Important things to remember for AP Stats (Topic 2.8): r² is about proportion of variance explained—it doesn’t tell you the direction of the relationship (that’s r) and it doesn’t prove causation. It also won’t tell you whether the line is a good model in context (check residuals and conditions, and beware of extrapolation). The least-squares line still minimizes the sum of squared residuals and goes through (x̄,ȳ). For a clear review, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj). For extra practice problems, try the AP practice bank (https://library.fiveable.me/practice/ap-statistics).
When do I use the formula b = r(sy/sx) vs just calculating slope normally?
Use b = r (s_y / s_x) whenever you already have the correlation r and the sample standard deviations s_x and s_y (or when the problem gives summary stats). That formula is exactly the least-squares slope (CED DAT-1.G.2)—it’s just a compact way to get the LSR slope from standardized info. If you have the raw (x,y) data and are computing by hand, you’ll usually use the “normal” slope formula for least squares: b = Σ(x_i − x̄)(y_i − ȳ) / Σ(x_i − x̄)^2, which is algebraically equivalent to r(s_y/s_x). On the AP exam you can use either; the formula sheet even lists b = r(s_y/s_x). If you use a graphing calculator’s linear regression function, it returns b directly (calculator allowed—bring one). For quick study/practice, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try problems on Fiveable’s practice page (https://library.fiveable.me/practice/ap-statistics).
How do I interpret the y-intercept when it doesn't make sense in context?
The y-intercept a is the predicted value of y when x = 0 (a = ȳ − b x̄), but the CED explicitly says “sometimes the y-intercept … does not have a logical interpretation in context” (DAT-1.G.3, DAT-1.H.3). If x = 0 is outside the range of your data or impossible (e.g., predicting height at age 0 when your sample is adults), say the intercept exists mathematically but is meaningless in context. On the AP exam, you should still: (1) state the intercept’s definition, (2) report its numerical value, and (3) explicitly say it’s not interpretable here and avoid using it to predict (extrapolation). Focus interpretation on slope and r² (how y changes per unit x and how much variation is explained). For a refresher, see Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
What does it mean that the regression line contains the point (x̄, ȳ)?
Saying the least-squares regression line contains the point (x̄, ȳ) means the fitted line always passes through the mean of the x-values and the mean of the y-values. Practically that gives you two handy facts: the intercept satisfies a = ȳ − b x̄, and the residuals sum to zero (which is one reason the LSR line minimizes the sum of squared residuals). This is a basic property of least-squares linear regression (CED DAT-1.G.1). Remember the slope formula b = r(s_y/s_x) and the model is ŷ = a + b x, so plugging x = x̄ yields ŷ = ȳ. For an AP tip, the formula sheet includes ŷ = a + b x and a = ȳ − b x̄—knowing this helps on free-response work. For a quick refresher check the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
Step by step how do I calculate the slope of a regression line using correlation?
Step-by-step: slope b from correlation r 1. Find r (sample correlation) for your paired data x and y. Use your calculator’s LinReg or the r formula (given on the AP formula sheet). 2. Compute sample standard deviations s_x and s_y (use 1/(n−1) formula or your calculator). 3. Plug into the AP CED formula: b = r · (s_y / s_x). That gives the slope in y-units per x-unit. 4. (Optional) Get the intercept a = ȳ − b x̄ so you can write ŷ = a + b x. Remember the least-squares line always goes through (x̄, ȳ). 5. Check reasonableness: sign of b matches sign of r; units make sense; don’t extrapolate beyond data. On the AP exam you can use a graphing calculator to compute r, means and s’s (bring an approved calculator). For a worked review, see Fiveable’s Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
Why does least squares regression minimize the sum of squared residuals?
Residual = observed y − predicted y. Least squares regression picks a and b for ŷ = a + bx to make the sum of squared residuals, Σ(yi − ŷi)², as small as possible. Squaring does two things: it makes all residuals positive so positive and negative errors don’t cancel, and it penalizes large errors more strongly so the line fits the bulk of the data. Algebraically, you set the partial derivatives of Σ(yi − a − bxi)² with respect to a and b to zero (the “normal equations”)—solving those gives the unique least-squares line that always passes through (x̄, ȳ) and yields b = r(sy/sx). This is exactly what the CED states: the least-squares model minimizes the sum of squared residuals and contains the mean point (DAT-1.G.1, DAT-1.G.2). For a quick study refresher, check the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and practice problems (https://library.fiveable.me/practice/ap-statistics).
How do I know if my y-intercept interpretation is logical or not?
The y-intercept a means the predicted y when x = 0 (a = ȳ − b x̄). To decide if that interpretation is logical, ask these quick checks: - Is x = 0 in your data’s range or a plausible value in context? If not, the intercept is extrapolation and likely meaningless. - Does the predicted y at x = 0 make sense with units and real-world limits (e.g., negative people, negative concentration)? If absurd, don’t interpret it. - Were there influential/extreme x-values driving the line? If yes, the intercept can be misleading. Check the scatterplot and residual plot for nonlinearity or outliers. - Even if x = 0 is possible, consider whether the linear model is appropriate near 0 (linearity and equal variance conditions). On the AP exam, you should state the intercept meaning only when x = 0 is within the scope and the value is sensible; otherwise say “no logical interpretation” (CED DAT-1.G.3 and DAT-1.H.3). For extra practice, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and more problems (https://library.fiveable.me/practice/ap-statistics).
What's the formula for the y-intercept and how do I use a = ȳ - bx̄?
The y-intercept formula is a = ȳ − b x̄. How you use it: 1. Find the sample means x̄ and ȳ (average of your x's and y's). 2. Get the slope b (use b = r·(s_y/s_x) if you have r and SDs, or let your calculator find the least-squares slope). 3. Plug into a = ȳ − b x̄ to compute the intercept a. That gives the regression line ŷ = a + b x. Why this works: the least-squares line always goes through the mean point (x̄, ȳ), so solving ȳ = a + b x̄ for a gives a = ȳ − b x̄ (CED DAT-1.G.1 & DAT-1.G.2). Interpret a as the predicted y when x = 0—but note (CED DAT-1.G.3) that x = 0 may be outside your data and then a may not make sense practically. For AP practice, the calculator is allowed on exam problems; review methods and examples in the Fiveable study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try extra problems (https://library.fiveable.me/practice/ap-statistics).
I don't understand what "proportion of variation explained" means for r squared
Think of r² as the percent of the response-variable’s total ups-and-downs that your linear model actually captures. In AP terms (CED DAT-1.G.4), r² is the coefficient of determination and equals the square of r in simple linear regression. More concretely: total variation in y = variation explained by the regression line + variation left in the residuals. r² = (variation explained) / (total variation). So r² = 0.64 means 64% of the variability in y is explained by x (your model), and 36% remains unexplained (randomness, other predictors, nonlinearity, measurement error). On the exam, interpret r² in context (e.g., “About 64% of the variation in test scores is explained by hours studied”), and note limitations (high r² doesn’t prove causation or that predictions are accurate outside the data). For a quick review, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj)—and try practice problems at (https://library.fiveable.me/practice/ap-statistics).
How do I calculate r squared from the correlation coefficient?
Square the correlation. r² = (r)(r). That’s it. r² is always nonnegative and gives the proportion of variation in y explained by x in the least-squares line (the coefficient of determination, per the CED DAT-1.G.4). Quick example: if r = −0.60, then r² = (−0.60)² = 0.36, so 36% of the variation in the response is explained by the explanatory variable. If r = 0.85, r² = 0.7225 → about 72.25% explained. On the AP exam you should state r² as a proportion or percent and interpret it in context (e.g., “about 36% of the variability in y is explained by x”). For more on least-squares and practice, check the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and Unit 2 review (https://library.fiveable.me/ap-statistics/unit-2). For extra practice problems, use Fiveable’s practice set (https://library.fiveable.me/practice/ap-statistics).
When the problem asks me to interpret the slope, what exactly should I say?
Say exactly how much the predicted response (y) changes when the explanatory variable (x) increases by one unit—and say it in context with units and direction. Quick checklist: - State “predicted [response variable] changes by [slope value] [units] for each 1 [unit of x] increase in [explanatory variable].” - Include sign: positive slope → increases; negative → decreases. - Mention “predicted” (because it’s a model) and keep it to the range of the data (no extrapolation). - If helpful, note magnitude: “about ___ more/less,” and round sensibly. Example phrasing: “For each additional year of education, predicted annual income increases by $2,500.” Or if slope = –0.70 in the CED example: “For each 1° north, predicted average low temperature decreases by 0.70°F.” You can mention slope formula b = r(s_y/s_x) when estimating or checking reasonableness (CED DAT-1.G.2). For extra review and practice phrasing, see the Topic 2.8 study guide (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and try practice problems (https://library.fiveable.me/practice/ap-statistics).
Can someone explain the difference between the actual slope formula and b = r(sy/sx)?
Short answer: they’re the same slope—b = r(sy/sx) is just a tidy form of the “actual” algebraic slope you get from the least-squares calculation. Why: the direct formula for the LS slope is b = [Σ(xi − x̄)(yi − ȳ)] / [Σ(xi − x̄)²]. If you rewrite the numerator using standardized scores and divide top and bottom by (n−1), you get r × (sy/sx). So b = r · (s_y / s_x). What that tells you conceptually: r sets the strength/direction (unitless, between −1 and 1) and s_y/s_x rescales that into y-units per x-unit. If r = 0 there’s no slope; if |r| = 1 then the slope magnitude is exactly sy/sx. When to use which: use the algebraic form if you’re computing from raw sums; use b = r(sy/sx) when you already have r, s_x, s_y (it’s the one listed in the AP CED). Remember the regression line goes through (x̄,ȳ) and intercept a = ȳ − b x̄. For more review and practice, see the Fiveable study guide on Least-Squares Regression (https://library.fiveable.me/ap-statistics/unit-2/least-squares-regression/study-guide/cRc4EhpHno3A4KvWrqyj) and lots of practice questions (https://library.fiveable.me/practice/ap-statistics).
