
7.5 Carrying Out a Test for a Population Mean
5 min read•march 31, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Calculating T-Scores
The first step in actually performing any statistical significance test is to calculate the test statistic used for that particular test. Since we are carrying out a significance test for a population mean, we should calculate a t-score. 💯
The t-score is a test statistic that is used in a t-test to evaluate the significance of the difference between the sample mean and a hypothesized population mean.
The t-score is calculated by dividing the difference between the sample mean and the hypothesized mean by the standard error of the mean. (The standard error of the mean is a measure of the variability of the sample mean and is calculated by dividing the standard deviation of the sample by the square root of the sample size.)
The larger the t-score, the more significant the difference between the sample mean and the hypothesized mean is.
When calculating a t-score, we use the general formula for critical values:
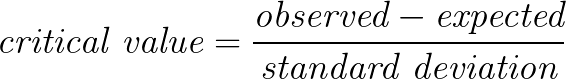
When we specify this formula for a t-score, we get the following:
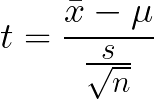
Where x̄ is our sample mean, 𝞵 is our hypothesized sample mean, s is our standard deviation of our sample and n is our sample size.
Example
Ricardo has a bag of 30 🍊s. The bag says that each orange weighs an average of 4.5 oz.
Ricardo weighs all of the oranges in his bag and finds that they have an average of 4.65 oz with a standard deviation of 0.8 oz.
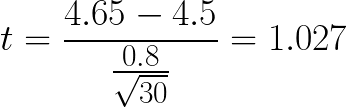
Calculating P-Value
When performing a hypothesis test, we could be performing either a one-tailed or two-tailed test. This depends on our alternate hypothesis when setting up our test. 🦊
The type of hypothesis test (one-tailed or two-tailed) is determined by the alternative hypothesis that you specify. If the alternative hypothesis is directional (e.g. "the population mean is greater than X"), then you would perform a one-tailed test because you're looking for a t-score only in one tail of our curve.
On the other hand, if the alternative hypothesis is non-directional (e.g. "the population mean is not equal to X"), then you would perform a two-tailed test since we are looking to find a t-score in either tail of our curve.
It's important to note that the choice of one-tailed or two-tailed test can have a significant impact on the results of the hypothesis test. A one-tailed test is more powerful than a two-tailed test because it allows you to detect a difference in a specific direction (e.g. the population mean is greater than X). However, this increased power comes at the cost of increased risk of a type I error (rejecting the null hypothesis when it is true). A two-tailed test is less powerful than a one-tailed test, but it reduces the risk of a type I error because it is not biased towards any particular direction. ✊
Back to the hypothesis test, we'll then need to reference our t-score chart to calculate our p value.
First, let's determine the degrees of freedom, which is always one less than our sample size.
Then, we find our t-score in the column matching our given degrees of freedom (df) to estimate our p-value. If the degrees of freedom can not be found in the chart, round down to the nearest df.
Example
In our example above with Ricardo's 🍊s, our df = 29. So we need to locate 29 df on the chart and then try to find 1.027.
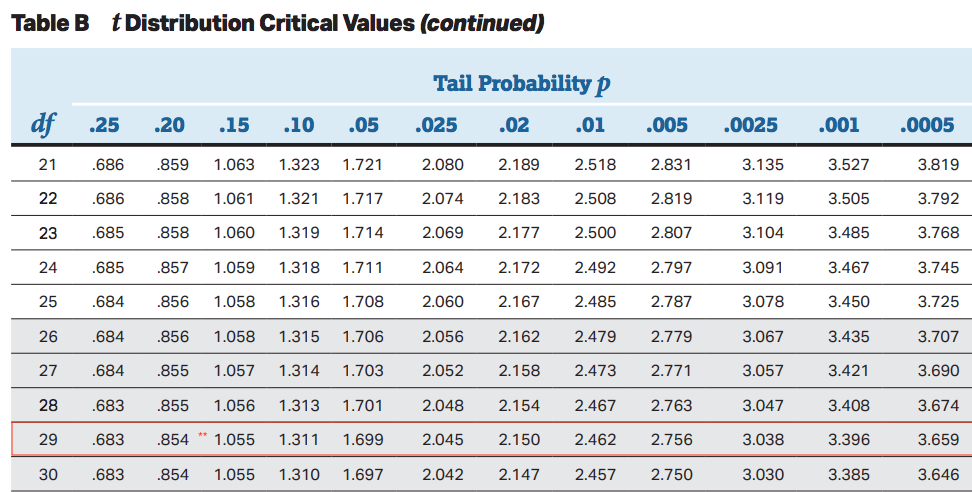
We can see in the t table, that the tail probability with df=29 and t-score of 1.027 is approximately 0.15 (since its close to 1.055).
If we are doing a one tailed test, this is our p-value.
If we are doing a two tailed test, we would double this to get 0.3 for our p-value (since the t curve is symmetric and tail probabilities are equal).
Using Calculator to Calculate T-Score and P-Value
Perhaps a much easier way to perform a one sample t test would be to use technology such as a graphing calculator. The most commonly used calculator for AP Statistics is the Texas Instruments TI-84. 📱
When performing a one sample t test, you will first enter into the stats menu:

Then, you will navigate over to tests and select option 2:

You are then given two options: you can enter the given sample statistics or let the calculator use data points entered in Lists to calculate your necessary test statistic and p value. We will proceed with our example using Ricardo's 🍊s.

Once you press calculate, it gives you your test statistic and p value. Both of these things are essential to list out in your written response to receive full credit on the AP exam. Also, it is important for a t-test for population mean to include your degrees of freedom, even though it is not listed in the computer output for the test.

Using P-Value to Make Conclusions
Once you have calculated the test statistic and p-value for your hypothesis test, you can use them to draw conclusions about the data. After all, the p-value is a measure of the likelihood of obtaining the observed results (or more extreme results) under the assumption that the null hypothesis is true. 🍀
If the p-value is less than the predetermined level of significance (usually 0.05), it means that the observed results are unlikely to have occurred by chance alone, and you can reject the null hypothesis in favor of the alternative hypothesis. On the other hand, if the p-value is greater than the level of significance, it means that the observed results are not statistically significant and you cannot reject the null hypothesis.
Templates
p < 𝞪: "Since p < 𝞪, we reject our Ho. We have convincing evidence at the 𝞪 level that (Ha in context of problem)."
p > 𝞪: "Since p > 𝞪, we fail reject our Ho. We do not have convincing evidence at the 𝞪 level that (Ha in context of problem)."
As always, we NEVER "accept" a null or alternate hypothesis. 🙅
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Means
Key Terms to Review (10)
degrees of freedom (df)
: Degrees of freedom refers to the number of values in a calculation that are free to vary without violating any constraints.Hypothesis Test
: A hypothesis test is a statistical procedure used to make decisions about whether there is enough evidence to support or reject a claim about a population parameter. It involves formulating null and alternative hypotheses, collecting data, and using statistical tests to evaluate those hypotheses.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Standard Deviation
: The standard deviation measures the average amount of variation or dispersion in a set of data. It tells us how spread out the values are from the mean.Standard Error of the Mean
: The standard error of the mean measures the variability or spread of sample means around the population mean. It helps us estimate how accurate our sample mean is as an estimate of the population mean.t-score
: A t-score is a statistical measure that represents how far a sample mean deviates from the population mean, in terms of standard error units. It is used to determine if there is a significant difference between the sample and population means.t-test
: A t-test is a statistical test that compares two sample means to determine if they are significantly different from each other.Texas Instruments TI-84
: The Texas Instruments TI-84 is a graphing calculator commonly used in high school mathematics and statistics courses. It allows students to perform various calculations, create graphs, and analyze data.7.5 Carrying Out a Test for a Population Mean
5 min read•march 31, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Calculating T-Scores
The first step in actually performing any statistical significance test is to calculate the test statistic used for that particular test. Since we are carrying out a significance test for a population mean, we should calculate a t-score. 💯
The t-score is a test statistic that is used in a t-test to evaluate the significance of the difference between the sample mean and a hypothesized population mean.
The t-score is calculated by dividing the difference between the sample mean and the hypothesized mean by the standard error of the mean. (The standard error of the mean is a measure of the variability of the sample mean and is calculated by dividing the standard deviation of the sample by the square root of the sample size.)
The larger the t-score, the more significant the difference between the sample mean and the hypothesized mean is.
When calculating a t-score, we use the general formula for critical values:
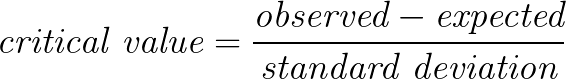
When we specify this formula for a t-score, we get the following:
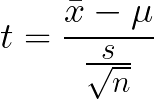
Where x̄ is our sample mean, 𝞵 is our hypothesized sample mean, s is our standard deviation of our sample and n is our sample size.
Example
Ricardo has a bag of 30 🍊s. The bag says that each orange weighs an average of 4.5 oz.
Ricardo weighs all of the oranges in his bag and finds that they have an average of 4.65 oz with a standard deviation of 0.8 oz.
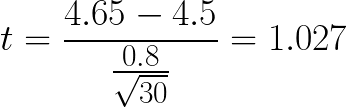
Calculating P-Value
When performing a hypothesis test, we could be performing either a one-tailed or two-tailed test. This depends on our alternate hypothesis when setting up our test. 🦊
The type of hypothesis test (one-tailed or two-tailed) is determined by the alternative hypothesis that you specify. If the alternative hypothesis is directional (e.g. "the population mean is greater than X"), then you would perform a one-tailed test because you're looking for a t-score only in one tail of our curve.
On the other hand, if the alternative hypothesis is non-directional (e.g. "the population mean is not equal to X"), then you would perform a two-tailed test since we are looking to find a t-score in either tail of our curve.
It's important to note that the choice of one-tailed or two-tailed test can have a significant impact on the results of the hypothesis test. A one-tailed test is more powerful than a two-tailed test because it allows you to detect a difference in a specific direction (e.g. the population mean is greater than X). However, this increased power comes at the cost of increased risk of a type I error (rejecting the null hypothesis when it is true). A two-tailed test is less powerful than a one-tailed test, but it reduces the risk of a type I error because it is not biased towards any particular direction. ✊
Back to the hypothesis test, we'll then need to reference our t-score chart to calculate our p value.
First, let's determine the degrees of freedom, which is always one less than our sample size.
Then, we find our t-score in the column matching our given degrees of freedom (df) to estimate our p-value. If the degrees of freedom can not be found in the chart, round down to the nearest df.
Example
In our example above with Ricardo's 🍊s, our df = 29. So we need to locate 29 df on the chart and then try to find 1.027.

We can see in the t table, that the tail probability with df=29 and t-score of 1.027 is approximately 0.15 (since its close to 1.055).
If we are doing a one tailed test, this is our p-value.
If we are doing a two tailed test, we would double this to get 0.3 for our p-value (since the t curve is symmetric and tail probabilities are equal).
Using Calculator to Calculate T-Score and P-Value
Perhaps a much easier way to perform a one sample t test would be to use technology such as a graphing calculator. The most commonly used calculator for AP Statistics is the Texas Instruments TI-84. 📱
When performing a one sample t test, you will first enter into the stats menu:

Then, you will navigate over to tests and select option 2:

You are then given two options: you can enter the given sample statistics or let the calculator use data points entered in Lists to calculate your necessary test statistic and p value. We will proceed with our example using Ricardo's 🍊s.

Once you press calculate, it gives you your test statistic and p value. Both of these things are essential to list out in your written response to receive full credit on the AP exam. Also, it is important for a t-test for population mean to include your degrees of freedom, even though it is not listed in the computer output for the test.

Using P-Value to Make Conclusions
Once you have calculated the test statistic and p-value for your hypothesis test, you can use them to draw conclusions about the data. After all, the p-value is a measure of the likelihood of obtaining the observed results (or more extreme results) under the assumption that the null hypothesis is true. 🍀
If the p-value is less than the predetermined level of significance (usually 0.05), it means that the observed results are unlikely to have occurred by chance alone, and you can reject the null hypothesis in favor of the alternative hypothesis. On the other hand, if the p-value is greater than the level of significance, it means that the observed results are not statistically significant and you cannot reject the null hypothesis.
Templates
p < 𝞪: "Since p < 𝞪, we reject our Ho. We have convincing evidence at the 𝞪 level that (Ha in context of problem)."
p > 𝞪: "Since p > 𝞪, we fail reject our Ho. We do not have convincing evidence at the 𝞪 level that (Ha in context of problem)."
As always, we NEVER "accept" a null or alternate hypothesis. 🙅
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Means
Key Terms to Review (10)
degrees of freedom (df)
: Degrees of freedom refers to the number of values in a calculation that are free to vary without violating any constraints.Hypothesis Test
: A hypothesis test is a statistical procedure used to make decisions about whether there is enough evidence to support or reject a claim about a population parameter. It involves formulating null and alternative hypotheses, collecting data, and using statistical tests to evaluate those hypotheses.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Standard Deviation
: The standard deviation measures the average amount of variation or dispersion in a set of data. It tells us how spread out the values are from the mean.Standard Error of the Mean
: The standard error of the mean measures the variability or spread of sample means around the population mean. It helps us estimate how accurate our sample mean is as an estimate of the population mean.t-score
: A t-score is a statistical measure that represents how far a sample mean deviates from the population mean, in terms of standard error units. It is used to determine if there is a significant difference between the sample and population means.t-test
: A t-test is a statistical test that compares two sample means to determine if they are significantly different from each other.Texas Instruments TI-84
: The Texas Instruments TI-84 is a graphing calculator commonly used in high school mathematics and statistics courses. It allows students to perform various calculations, create graphs, and analyze data.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.