
6.10 Setting Up a Test for the Difference of Two Population Proportions
4 min read•january 3, 2023
Harrison Burnside
Jed Quiaoit
Harrison Burnside
Jed Quiaoit
Another way to check a statistical claim is to perform a for the difference in two population proportions. As with any , we have to write hypotheses, check our conditions and then calculate and conclude. 📲
Still lost? Let's do a refresher!
A statistical is used to determine whether the difference between two population proportions is statistically significant, or whether it could have occurred by chance.
To perform a for the difference in two population proportions, you need to first write your null and alternative hypotheses. The null hypothesis states that there is no difference between the two population proportions, while the states that there is a difference.
Next, you need to check that the conditions for the test are met. These include having a large enough and having a random and independent sample.
Once you have checked the conditions, you can calculate the and determine the . The is the probability of obtaining a as extreme as the one observed, given that the null hypothesis is true. If the is less than the (usually 0.05), you can reject the null hypothesis and conclude that the difference between the two population proportions is statistically significant. If the is greater than the , you cannot reject the null hypothesis and must conclude that the difference is not statistically significant. 😄
Hypotheses and Parameters
The first thing we need to do when setting up a for the difference in two population proportions is to write out our hypotheses. Our null hypotheses will always have our two population proportions being equal, while our alternate has them either greater than, less than or not equal to each other. 🏆

It is also important in this stage of setting up the test to identify what p1 and p2 represent. We have to define our parameters so the reader knows what we are truly comparing.
Conditions
We also must check our conditions for inference. The same three conditions apply as did for confidence intervals with one little small change in the normal check.
(1) Random
Probably the most important condition is that we need to be sure that both of our samples come from random samples. If we don't take a from our population, then our findings suffer from and we are stuck and we can't generalize our findings to our population. 😞
(2) Independence
To check that our sample is independent, we need to make sure that both of our populations are at least 10 times that of our samples. Also, if we are dealing with a randomized experiment, the random assignment of treatments classifies our samples as independently selected. 🔟
(3) Normal
When dealing with proportions, we always check our normal condition by using the , which states that our expected successes and failures is at least 10. With a , we have to combine our proportions to create a combined p-hat. This is what we use to find our expected failures and successes. 🎩
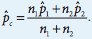
Then we have to verify that each of our expected failures and successes are at least 10.
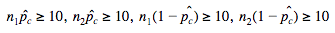
This is because we are using a pooled sample. In this test, you combine the two samples into a single "pooled" sample and calculate a single proportion for the combined sample. The is then calculated based on the difference between the two proportions and the proportion. 🏊
Example
Let's return to our MJ vs. Lebron problem from earlier... again. Recall that MJ made 836/1623 shots and Lebron made 622/1493 shots. Instead of testing this claim with a , let's test it using a 2 Prop Z Test to verify our results. 🏀
Hypotheses and Parameters

Another great idea when writing our hypotheses is to use meaningful subscripts such as MJ and L that clarify which proportion matches which population.
Conditions
Random: Even though the problem never stated that they were random (and we discussed the problems with this in Unit 6.9) we are going to assume it is random.
Independent: It is reasonable to believe (and obviously true) that MJ took at least 16, 230 shots in his career and Lebron took at least 14,930 shots in his career, so the samples are independent.
Normal: This is the one that will be a bit different. First, we have to calculate our pooled p-hat. Using the formula above, we get 0.468

Next, we have to check our using this pooled p-hat.
1623 (0.468) > 10 ✔️
1623 (0.532) > 10 ✔️
1493 (0.468) > 10 ✔️
1493 (0.532) > 10 ✔️
Now that we have checked conditions, we are ready to calculate and test our claim. 🧪
🎥 Watch: AP Stats - Inference: Hypothesis tests for Proportions
Key Terms to Review (13)
2 Proportion Z Test
: The 2 proportion z test is a hypothesis test used to compare two proportions from independent samples. It determines whether there is enough evidence to conclude that the proportions are significantly different from each other.Alternative Hypothesis
: The alternative hypothesis is a statement that contradicts or negates the null hypothesis. It suggests that there is a significant relationship or difference between variables.Confidence Interval
: A confidence interval is a range of values that is likely to contain the true value of a population parameter. It provides an estimate along with a level of confidence about how accurate the estimate is.Independent Sample
: An independent sample refers to a group of observations or data points that are not related or dependent on each other. Each observation is selected randomly and does not influence the selection of other observations.Large Counts Condition
: The large counts condition, also known as the "success-failure" condition, is used when applying certain statistical methods to categorical data. It states that for these methods to be valid, both the number of successes and failures must be at least 10.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Pooled Sample
: A pooled sample is a combined sample that includes data from two or more groups or populations. It is often used in hypothesis testing to estimate the common standard deviation for the groups being compared.Random Sample
: A random sample is a subset of individuals selected from a larger population in such a way that every individual has an equal chance of being chosen. It helps to ensure that the sample is representative of the population.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Sampling Bias
: Sampling bias occurs when the sample selected for a study is not representative of the population, leading to inaccurate or misleading results.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Significance Test
: A significance test is a statistical method used to determine whether an observed result is statistically significant or simply due to chance. It involves comparing sample data with what would be expected under the null hypothesis.Test Statistic
: A test statistic is a numerical value calculated from sample data that is used to make inferences about a population parameter. It measures the discrepancy between the observed data and what would be expected under a specific hypothesis.6.10 Setting Up a Test for the Difference of Two Population Proportions
4 min read•january 3, 2023
Harrison Burnside
Jed Quiaoit
Harrison Burnside
Jed Quiaoit
Another way to check a statistical claim is to perform a for the difference in two population proportions. As with any , we have to write hypotheses, check our conditions and then calculate and conclude. 📲
Still lost? Let's do a refresher!
A statistical is used to determine whether the difference between two population proportions is statistically significant, or whether it could have occurred by chance.
To perform a for the difference in two population proportions, you need to first write your null and alternative hypotheses. The null hypothesis states that there is no difference between the two population proportions, while the states that there is a difference.
Next, you need to check that the conditions for the test are met. These include having a large enough and having a random and independent sample.
Once you have checked the conditions, you can calculate the and determine the . The is the probability of obtaining a as extreme as the one observed, given that the null hypothesis is true. If the is less than the (usually 0.05), you can reject the null hypothesis and conclude that the difference between the two population proportions is statistically significant. If the is greater than the , you cannot reject the null hypothesis and must conclude that the difference is not statistically significant. 😄
Hypotheses and Parameters
The first thing we need to do when setting up a for the difference in two population proportions is to write out our hypotheses. Our null hypotheses will always have our two population proportions being equal, while our alternate has them either greater than, less than or not equal to each other. 🏆

It is also important in this stage of setting up the test to identify what p1 and p2 represent. We have to define our parameters so the reader knows what we are truly comparing.
Conditions
We also must check our conditions for inference. The same three conditions apply as did for confidence intervals with one little small change in the normal check.
(1) Random
Probably the most important condition is that we need to be sure that both of our samples come from random samples. If we don't take a from our population, then our findings suffer from and we are stuck and we can't generalize our findings to our population. 😞
(2) Independence
To check that our sample is independent, we need to make sure that both of our populations are at least 10 times that of our samples. Also, if we are dealing with a randomized experiment, the random assignment of treatments classifies our samples as independently selected. 🔟
(3) Normal
When dealing with proportions, we always check our normal condition by using the , which states that our expected successes and failures is at least 10. With a , we have to combine our proportions to create a combined p-hat. This is what we use to find our expected failures and successes. 🎩
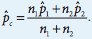
Then we have to verify that each of our expected failures and successes are at least 10.
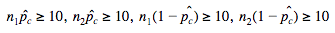
This is because we are using a pooled sample. In this test, you combine the two samples into a single "pooled" sample and calculate a single proportion for the combined sample. The is then calculated based on the difference between the two proportions and the proportion. 🏊
Example
Let's return to our MJ vs. Lebron problem from earlier... again. Recall that MJ made 836/1623 shots and Lebron made 622/1493 shots. Instead of testing this claim with a , let's test it using a 2 Prop Z Test to verify our results. 🏀
Hypotheses and Parameters

Another great idea when writing our hypotheses is to use meaningful subscripts such as MJ and L that clarify which proportion matches which population.
Conditions
Random: Even though the problem never stated that they were random (and we discussed the problems with this in Unit 6.9) we are going to assume it is random.
Independent: It is reasonable to believe (and obviously true) that MJ took at least 16, 230 shots in his career and Lebron took at least 14,930 shots in his career, so the samples are independent.
Normal: This is the one that will be a bit different. First, we have to calculate our pooled p-hat. Using the formula above, we get 0.468

Next, we have to check our using this pooled p-hat.
1623 (0.468) > 10 ✔️
1623 (0.532) > 10 ✔️
1493 (0.468) > 10 ✔️
1493 (0.532) > 10 ✔️
Now that we have checked conditions, we are ready to calculate and test our claim. 🧪
🎥 Watch: AP Stats - Inference: Hypothesis tests for Proportions
Key Terms to Review (13)
2 Proportion Z Test
: The 2 proportion z test is a hypothesis test used to compare two proportions from independent samples. It determines whether there is enough evidence to conclude that the proportions are significantly different from each other.Alternative Hypothesis
: The alternative hypothesis is a statement that contradicts or negates the null hypothesis. It suggests that there is a significant relationship or difference between variables.Confidence Interval
: A confidence interval is a range of values that is likely to contain the true value of a population parameter. It provides an estimate along with a level of confidence about how accurate the estimate is.Independent Sample
: An independent sample refers to a group of observations or data points that are not related or dependent on each other. Each observation is selected randomly and does not influence the selection of other observations.Large Counts Condition
: The large counts condition, also known as the "success-failure" condition, is used when applying certain statistical methods to categorical data. It states that for these methods to be valid, both the number of successes and failures must be at least 10.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Pooled Sample
: A pooled sample is a combined sample that includes data from two or more groups or populations. It is often used in hypothesis testing to estimate the common standard deviation for the groups being compared.Random Sample
: A random sample is a subset of individuals selected from a larger population in such a way that every individual has an equal chance of being chosen. It helps to ensure that the sample is representative of the population.Sample Size
: The sample size refers to the number of individuals or observations included in a study or experiment.Sampling Bias
: Sampling bias occurs when the sample selected for a study is not representative of the population, leading to inaccurate or misleading results.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Significance Test
: A significance test is a statistical method used to determine whether an observed result is statistically significant or simply due to chance. It involves comparing sample data with what would be expected under the null hypothesis.Test Statistic
: A test statistic is a numerical value calculated from sample data that is used to make inferences about a population parameter. It measures the discrepancy between the observed data and what would be expected under a specific hypothesis.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.