
6.8 Confidence Intervals for the Difference of Two Proportions
5 min read•january 3, 2023
Jed Quiaoit
Josh Argo
Jed Quiaoit
Josh Argo
Two-Sample Z-Intervals
Have you ever seen two athletes and wondered how much better one was than the other? Maybe a basketball player who is really good at three pointers and another who seems to be just as good. How can you tell if one is actually better than the other? 🏀
One way to look at that is to determine what the difference in their shot percentage is by using a confidence interval. A confidence interval will give us a range of numbers that the difference in their percentages will be within.
The appropriate confidence interval procedure for a two-sample comparison of proportions for one categorical variable is a two-sample z-interval for a difference between .
In other words, a two-sample z-interval can be used to compare the proportions of a categorical variable between two independent populations. The procedure involves constructing a confidence interval for the difference between the two using the , sample sizes, and standard errors.
To construct a two-sample z-interval, the following steps should be taken:
Calculate the for each population: p̂1 and p̂2
Calculate the for the difference between the two : SE = √(p̂1(1-p̂1)/n1 + p̂2(1-p̂2)/n2) -- a clearer version of the formula is available in the image all the way down
Calculate the for the desired confidence level: zα/2
Calculate the lower and upper limits of the confidence interval: p̂1 - p̂2 ± zα/2 * SE
The resulting confidence interval will provide an estimate of the true difference between the , with a certain level of confidence (determined by the chosen confidence level). If the of no difference between the is true, the interval should contain 0. If the interval does not contain 0, then the can be rejected and we can conclude that there is a difference between the . We'll work or interpretations more in a future section, don't worry! 😉
Necessary Conditions
As with any forms of inference, we have some necessary conditions to check. These are essential anytime we are using a sample to make an inference about a population.
(1) Random
Probably the most important condition is that we need to be sure that both of our samples come from random samples. If we don't take a random sample from our population, then our findings suffer from and we are stuck and we can't generalize our findings to our population. 😞
(2) Independence
To check that our sample is independent, we need to make sure that both of our populations are at least 10 times that of our samples. Also, if we are dealing with a randomized experiment, the random assignment of treatments classifies our samples as independently selected. 🔟
(3) Normal
When dealing with proportions, we always check our normal condition by using the , which states that our expected successes and failures is at least 10. Since we have two samples in this type of test, we have to check this condition for both samples. In other words, 🔔
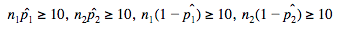
This verifies that our confidence interval is based off of a .
How Do I Calculate?
As I am sure you remember from Unit 6.2, a confidence interval is based on two aspects: a and a . A confidence interval for the difference of two is no different. 😲
(1) Point Estimate
In the case of a confidence interval for two proportions, the is the difference in our two . We can find this by simply subtracting the two , or p-hats.
(2) Margin of Error
As before, our is the "buffer zone" that we add and subtract to our to be sure that our interval encompasses our true population proportion difference. This is based off of two things: our critical value () and our standard error.
Formula
Our overall formula as found on the AP Statistics Course Exam Description looks like this:

image courtesy of: apcentral.collegeboard.org
Using a Calculator
A much more efficient way of calculating a confidence interval for the difference of two is to use some form of technology such as a . On most common calculators, you will select "" from the Stats/Tests menu. 😌
Example
The-age old argument of Michael Jordan vs. Lebron James has risen again. In an effort to prove your point, you take their two career shots made percentages to see if they are REALLY different. To test this claim, you decide to construct a confidence interval for the difference in their proportion of shots. We take a sample of MJ shots and Lebron's shots from their first season in NBA. According to basketball-reference.com, MJ attempted 1623 field goals his first season, making 836 of them. Lebron attempted 1493 field goals, making 622 of his shots. Construct and interpret a 95% confidence interval to determine their difference in proportions of shots made. ☄️
Conditions
Random: Since the problem looked at their first season, we will assume they were "randomly chosen." Sometimes, problems don't specify that it was randomly selected so we have to assume they were and proceed.
Independent: Since it is reasonable to believe that MJ took at least 16,230 shots in his career and Lebron has taken at least 14,930 shots, we will say they are independent samples.
Normal: Both MJ and Lebron had at least 10 makes and misses from their samples, so we can use a normal approximation for the sampling distribution of the difference in their proportion of shots made.
Do Calculations
Using a calculator for our calculations, we entered our data into ""
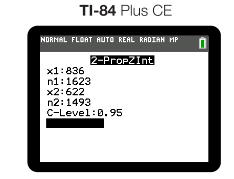
Which gives us the following interval:

To find out more about how to interpret this interval, click ahead to Unit 6.9...
🎥 Watch: AP Stats - Inference: Confidence Intervals for Proportions
Key Terms to Review (16)
2 Prop Z Interval
: The "2 Prop Z Interval" is a confidence interval used for comparing two proportions. It estimates the difference between two population proportions based on sample data.Critical Value
: A critical value is a specific value that separates the rejection region from the non-rejection region in hypothesis testing. It is compared to the test statistic to determine whether to reject or fail to reject the null hypothesis.Graphing Calculator
: A graphing calculator is an electronic device that can perform various mathematical calculations and display graphs. It is commonly used in statistics to visualize data, solve equations, and perform statistical analyses.Independence Condition
: The independence condition states that for statistical inference methods to be valid, observations must be independent of each other. In other words, knowing the outcome or value of one observation should not provide any information about another observation.Large Counts Condition
: The large counts condition, also known as the "success-failure" condition, is used when applying certain statistical methods to categorical data. It states that for these methods to be valid, both the number of successes and failures must be at least 10.Margin of Error
: The margin of error is a measure of the uncertainty or variability in survey results. It represents the range within which the true population parameter is likely to fall.Normal Sampling Distribution
: A normal sampling distribution is a theoretical distribution that represents the possible values of a statistic, such as the mean or proportion, when repeated random samples are taken from a population. It follows a bell-shaped curve and is characterized by its mean and standard deviation.Null Hypothesis
: The null hypothesis is a statement of no effect or relationship between variables in a statistical analysis. It assumes that any observed differences or associations are due to random chance.Point Estimate
: A point estimate is a single value that is used to estimate an unknown population parameter. It is obtained from sample data and serves as our best guess for the true value of the parameter.Population Proportions
: Population proportions refer to the proportion or percentage of a specific characteristic or attribute within an entire population.Random Sampling
: Random sampling is a method of selecting individuals from a population in such a way that every individual has an equal chance of being chosen. It helps to ensure that the sample represents the population accurately.Sample Proportions
: Sample proportions refer to the proportion or percentage of a specific characteristic or outcome within a sample. It is calculated by dividing the number of individuals with that characteristic by the total number of individuals in the sample.Sampling Bias
: Sampling bias occurs when the sample selected for a study is not representative of the population, leading to inaccurate or misleading results.Standard Error
: The standard error is a measure of the variability or spread of sample means around the population mean. It tells us how much we can expect sample means to differ from the true population mean.Two-Sample Z-Intervals
: Two-Sample Z-Intervals are used to estimate the difference between two population means when we have data from two independent samples. It helps us determine a range of values within which the true difference between the means is likely to fall.Z-Score
: A z-score is a measure of how many standard deviations an individual data point is away from the mean of a distribution. It helps to determine the relative position of a data point within a dataset.6.8 Confidence Intervals for the Difference of Two Proportions
5 min read•january 3, 2023
Jed Quiaoit
Josh Argo
Jed Quiaoit
Josh Argo
Two-Sample Z-Intervals
Have you ever seen two athletes and wondered how much better one was than the other? Maybe a basketball player who is really good at three pointers and another who seems to be just as good. How can you tell if one is actually better than the other? 🏀
One way to look at that is to determine what the difference in their shot percentage is by using a confidence interval. A confidence interval will give us a range of numbers that the difference in their percentages will be within.
The appropriate confidence interval procedure for a two-sample comparison of proportions for one categorical variable is a two-sample z-interval for a difference between .
In other words, a two-sample z-interval can be used to compare the proportions of a categorical variable between two independent populations. The procedure involves constructing a confidence interval for the difference between the two using the , sample sizes, and standard errors.
To construct a two-sample z-interval, the following steps should be taken:
Calculate the for each population: p̂1 and p̂2
Calculate the for the difference between the two : SE = √(p̂1(1-p̂1)/n1 + p̂2(1-p̂2)/n2) -- a clearer version of the formula is available in the image all the way down
Calculate the for the desired confidence level: zα/2
Calculate the lower and upper limits of the confidence interval: p̂1 - p̂2 ± zα/2 * SE
The resulting confidence interval will provide an estimate of the true difference between the , with a certain level of confidence (determined by the chosen confidence level). If the of no difference between the is true, the interval should contain 0. If the interval does not contain 0, then the can be rejected and we can conclude that there is a difference between the . We'll work or interpretations more in a future section, don't worry! 😉
Necessary Conditions
As with any forms of inference, we have some necessary conditions to check. These are essential anytime we are using a sample to make an inference about a population.
(1) Random
Probably the most important condition is that we need to be sure that both of our samples come from random samples. If we don't take a random sample from our population, then our findings suffer from and we are stuck and we can't generalize our findings to our population. 😞
(2) Independence
To check that our sample is independent, we need to make sure that both of our populations are at least 10 times that of our samples. Also, if we are dealing with a randomized experiment, the random assignment of treatments classifies our samples as independently selected. 🔟
(3) Normal
When dealing with proportions, we always check our normal condition by using the , which states that our expected successes and failures is at least 10. Since we have two samples in this type of test, we have to check this condition for both samples. In other words, 🔔
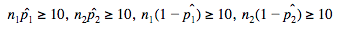
This verifies that our confidence interval is based off of a .
How Do I Calculate?
As I am sure you remember from Unit 6.2, a confidence interval is based on two aspects: a and a . A confidence interval for the difference of two is no different. 😲
(1) Point Estimate
In the case of a confidence interval for two proportions, the is the difference in our two . We can find this by simply subtracting the two , or p-hats.
(2) Margin of Error
As before, our is the "buffer zone" that we add and subtract to our to be sure that our interval encompasses our true population proportion difference. This is based off of two things: our critical value () and our standard error.
Formula
Our overall formula as found on the AP Statistics Course Exam Description looks like this:

image courtesy of: apcentral.collegeboard.org
Using a Calculator
A much more efficient way of calculating a confidence interval for the difference of two is to use some form of technology such as a . On most common calculators, you will select "" from the Stats/Tests menu. 😌
Example
The-age old argument of Michael Jordan vs. Lebron James has risen again. In an effort to prove your point, you take their two career shots made percentages to see if they are REALLY different. To test this claim, you decide to construct a confidence interval for the difference in their proportion of shots. We take a sample of MJ shots and Lebron's shots from their first season in NBA. According to basketball-reference.com, MJ attempted 1623 field goals his first season, making 836 of them. Lebron attempted 1493 field goals, making 622 of his shots. Construct and interpret a 95% confidence interval to determine their difference in proportions of shots made. ☄️
Conditions
Random: Since the problem looked at their first season, we will assume they were "randomly chosen." Sometimes, problems don't specify that it was randomly selected so we have to assume they were and proceed.
Independent: Since it is reasonable to believe that MJ took at least 16,230 shots in his career and Lebron has taken at least 14,930 shots, we will say they are independent samples.
Normal: Both MJ and Lebron had at least 10 makes and misses from their samples, so we can use a normal approximation for the sampling distribution of the difference in their proportion of shots made.
Do Calculations
Using a calculator for our calculations, we entered our data into ""

Which gives us the following interval:

To find out more about how to interpret this interval, click ahead to Unit 6.9...
🎥 Watch: AP Stats - Inference: Confidence Intervals for Proportions
Key Terms to Review (16)
2 Prop Z Interval
: The "2 Prop Z Interval" is a confidence interval used for comparing two proportions. It estimates the difference between two population proportions based on sample data.Critical Value
: A critical value is a specific value that separates the rejection region from the non-rejection region in hypothesis testing. It is compared to the test statistic to determine whether to reject or fail to reject the null hypothesis.Graphing Calculator
: A graphing calculator is an electronic device that can perform various mathematical calculations and display graphs. It is commonly used in statistics to visualize data, solve equations, and perform statistical analyses.Independence Condition
: The independence condition states that for statistical inference methods to be valid, observations must be independent of each other. In other words, knowing the outcome or value of one observation should not provide any information about another observation.Large Counts Condition
: The large counts condition, also known as the "success-failure" condition, is used when applying certain statistical methods to categorical data. It states that for these methods to be valid, both the number of successes and failures must be at least 10.Margin of Error
: The margin of error is a measure of the uncertainty or variability in survey results. It represents the range within which the true population parameter is likely to fall.Normal Sampling Distribution
: A normal sampling distribution is a theoretical distribution that represents the possible values of a statistic, such as the mean or proportion, when repeated random samples are taken from a population. It follows a bell-shaped curve and is characterized by its mean and standard deviation.Null Hypothesis
: The null hypothesis is a statement of no effect or relationship between variables in a statistical analysis. It assumes that any observed differences or associations are due to random chance.Point Estimate
: A point estimate is a single value that is used to estimate an unknown population parameter. It is obtained from sample data and serves as our best guess for the true value of the parameter.Population Proportions
: Population proportions refer to the proportion or percentage of a specific characteristic or attribute within an entire population.Random Sampling
: Random sampling is a method of selecting individuals from a population in such a way that every individual has an equal chance of being chosen. It helps to ensure that the sample represents the population accurately.Sample Proportions
: Sample proportions refer to the proportion or percentage of a specific characteristic or outcome within a sample. It is calculated by dividing the number of individuals with that characteristic by the total number of individuals in the sample.Sampling Bias
: Sampling bias occurs when the sample selected for a study is not representative of the population, leading to inaccurate or misleading results.Standard Error
: The standard error is a measure of the variability or spread of sample means around the population mean. It tells us how much we can expect sample means to differ from the true population mean.Two-Sample Z-Intervals
: Two-Sample Z-Intervals are used to estimate the difference between two population means when we have data from two independent samples. It helps us determine a range of values within which the true difference between the means is likely to fall.Z-Score
: A z-score is a measure of how many standard deviations an individual data point is away from the mean of a distribution. It helps to determine the relative position of a data point within a dataset.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.