
6.11 Carrying Out a Test for the Difference of Two Population Proportions
4 min read•january 3, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Calculating Values
There are two important values that we need to calculate in order to carry out a test for the difference in two population proportions. We need to calculate a and a . Both need to be included in our response to inference-related FRQs to receive full credit. 💯
Z-Score
The for our test is our critical value. We can calculate it by using the formula for any :
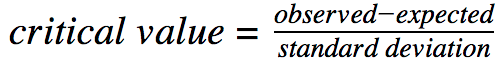

That formula looks pretty icky. 🤢 Luckily if we run our test on a calculator, the is part of our calculator output.
P-Value
As with any , we are using the normal curve and our to calculate the probability of obtaining such a value (or one less than/greater than) that value. Also, using a calculator here is much easier than doing it by hand.
Concluding the Test
Once we have our and , we can then make a judgment to either reject or fail to reject our . ✋
Using P-Value
If you are using a to perform a significance test for the difference in two population proportions, you compare the to the to determine whether to . The is the probability of rejecting the when it is actually true. It is usually set at 0.05, which means that there is a 5% chance of rejecting the when it is actually true.
If the is less than the , it means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. This gives you reason to and conclude that there is a difference between the two population proportions. This means that it was an extremely rare occurrence (WOW value!) and we have reason to believe our (center of our ) wasn't accurate.
On the other hand, if the is greater than the , it means that the difference is not statistically significant and may have occurred by chance. In this case, you cannot and must conclude that there is no difference between the two population proportions.
Therefore, if the p is low, reject the H0.
Using Z-Score
If you are using a to perform a significance test for the difference in two population proportions, you can use the to determine whether the represents an extremely rare value on the . The states that for a normal distribution, approximately 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations. ⭐
So if the is higher than 2 or 3, it is considered an extremely rare value on the , and you can with a high degree of confidence. This means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. On the other hand, if the is less than 2 or 3, it is not considered an extremely rare value and you cannot reject the . This means that the difference between the two population proportions is not statistically significant and may have occurred by chance. 🍀
Continued Example
Let's continue our example of MJ vs. Lebron to see if we can verify our conclusion from Unit 6.9. Recall that Michael Jordan made 836/1623 shots and Lebron James made 622/1493 shots. We are seeing if our data gives significant statistical evidence that Michael Jordan is actually better than Lebron. 🏀
Calculations
To avoid the lengthy and cumbersome formulas above, we are going to use a graphing calculator and the appropriate "2 Prop Z Test" to test our hypothesis:

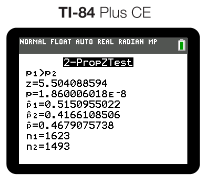
The two big values that we need to write down from our output is our and .
Conclusion
To conclude our test, we can look at how low our is, or how high our is. ➡️
P-Value
Our is the best way to conclude. In this problem, we can see that our is essentially 0. Therefore, we can say:
"Since our is less than 0.05 (~0 < 0.05), we reject our Ho. We have convincing evidence that the true population proportion of shots made by MJ is higher than the true population proportion of shots made by Lebron."
Notice that this supports our conclusion from the . ✔️
Z-Score
If not given the data to calculate a or if only given the , we can still make a judgment on the . In the example above, we end up with a of 5.5, which is pretty extreme. Therefore, we can conclude that we can reject our in favor of our alternate hypothesis! ✔️
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions
Key Terms to Review (8)
Confidence Interval
: A confidence interval is a range of values that is likely to contain the true value of a population parameter. It provides an estimate along with a level of confidence about how accurate the estimate is.Empirical Rule
: The empirical rule, also known as the 68-95-99.7 rule, is a statistical guideline that states that for a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and roughly 99.7% falls within three standard deviations.Null Hypothesis
: The null hypothesis is a statement of no effect or relationship between variables in a statistical analysis. It assumes that any observed differences or associations are due to random chance.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Reject the Null Hypothesis
: When conducting a hypothesis test, rejecting the null hypothesis means that there is enough evidence to support the alternative hypothesis. In other words, it suggests that there is a significant difference or relationship between variables.Sampling Distribution
: A sampling distribution refers to the distribution of a statistic (such as mean, proportion, or difference) calculated from multiple random samples taken from the same population. It provides information about how sample statistics vary from sample to sample.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Z-Score
: A z-score is a measure of how many standard deviations an individual data point is away from the mean of a distribution. It helps to determine the relative position of a data point within a dataset.6.11 Carrying Out a Test for the Difference of Two Population Proportions
4 min read•january 3, 2023
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Calculating Values
There are two important values that we need to calculate in order to carry out a test for the difference in two population proportions. We need to calculate a and a . Both need to be included in our response to inference-related FRQs to receive full credit. 💯
Z-Score
The for our test is our critical value. We can calculate it by using the formula for any :
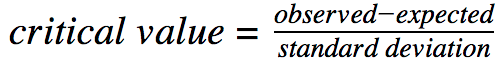

That formula looks pretty icky. 🤢 Luckily if we run our test on a calculator, the is part of our calculator output.
P-Value
As with any , we are using the normal curve and our to calculate the probability of obtaining such a value (or one less than/greater than) that value. Also, using a calculator here is much easier than doing it by hand.
Concluding the Test
Once we have our and , we can then make a judgment to either reject or fail to reject our . ✋
Using P-Value
If you are using a to perform a significance test for the difference in two population proportions, you compare the to the to determine whether to . The is the probability of rejecting the when it is actually true. It is usually set at 0.05, which means that there is a 5% chance of rejecting the when it is actually true.
If the is less than the , it means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. This gives you reason to and conclude that there is a difference between the two population proportions. This means that it was an extremely rare occurrence (WOW value!) and we have reason to believe our (center of our ) wasn't accurate.
On the other hand, if the is greater than the , it means that the difference is not statistically significant and may have occurred by chance. In this case, you cannot and must conclude that there is no difference between the two population proportions.
Therefore, if the p is low, reject the H0.
Using Z-Score
If you are using a to perform a significance test for the difference in two population proportions, you can use the to determine whether the represents an extremely rare value on the . The states that for a normal distribution, approximately 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations. ⭐
So if the is higher than 2 or 3, it is considered an extremely rare value on the , and you can with a high degree of confidence. This means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. On the other hand, if the is less than 2 or 3, it is not considered an extremely rare value and you cannot reject the . This means that the difference between the two population proportions is not statistically significant and may have occurred by chance. 🍀
Continued Example
Let's continue our example of MJ vs. Lebron to see if we can verify our conclusion from Unit 6.9. Recall that Michael Jordan made 836/1623 shots and Lebron James made 622/1493 shots. We are seeing if our data gives significant statistical evidence that Michael Jordan is actually better than Lebron. 🏀
Calculations
To avoid the lengthy and cumbersome formulas above, we are going to use a graphing calculator and the appropriate "2 Prop Z Test" to test our hypothesis:


The two big values that we need to write down from our output is our and .
Conclusion
To conclude our test, we can look at how low our is, or how high our is. ➡️
P-Value
Our is the best way to conclude. In this problem, we can see that our is essentially 0. Therefore, we can say:
"Since our is less than 0.05 (~0 < 0.05), we reject our Ho. We have convincing evidence that the true population proportion of shots made by MJ is higher than the true population proportion of shots made by Lebron."
Notice that this supports our conclusion from the . ✔️
Z-Score
If not given the data to calculate a or if only given the , we can still make a judgment on the . In the example above, we end up with a of 5.5, which is pretty extreme. Therefore, we can conclude that we can reject our in favor of our alternate hypothesis! ✔️
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions
Key Terms to Review (8)
Confidence Interval
: A confidence interval is a range of values that is likely to contain the true value of a population parameter. It provides an estimate along with a level of confidence about how accurate the estimate is.Empirical Rule
: The empirical rule, also known as the 68-95-99.7 rule, is a statistical guideline that states that for a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and roughly 99.7% falls within three standard deviations.Null Hypothesis
: The null hypothesis is a statement of no effect or relationship between variables in a statistical analysis. It assumes that any observed differences or associations are due to random chance.P-value
: The p-value is a probability value that helps determine whether an observed result is statistically significant or occurred by chance. It quantifies how strong or weak evidence against a null hypothesis exists.Reject the Null Hypothesis
: When conducting a hypothesis test, rejecting the null hypothesis means that there is enough evidence to support the alternative hypothesis. In other words, it suggests that there is a significant difference or relationship between variables.Sampling Distribution
: A sampling distribution refers to the distribution of a statistic (such as mean, proportion, or difference) calculated from multiple random samples taken from the same population. It provides information about how sample statistics vary from sample to sample.Significance Level
: The significance level, also known as alpha (α), determines how much evidence we need to reject the null hypothesis. It represents the probability of making a Type I error.Z-Score
: A z-score is a measure of how many standard deviations an individual data point is away from the mean of a distribution. It helps to determine the relative position of a data point within a dataset.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.