
2.9 Analyzing Departures from Linearity
6 min read•december 29, 2022
Athena_Codes
Jed Quiaoit
Athena_Codes
Jed Quiaoit
Sometimes, the least squares regression model may not be the best for representing a data set. We’re going to list some reasons why. While we briefly introduced them in section 2.4, we'll go into further detail here.
Influential Points
An influential point is a point that when added, significantly changes the regression model, whether by affecting the slope, y-intercept, or correlation. There are two types: outliers and high-leverage points, which are both shown in this graph. ⚒️
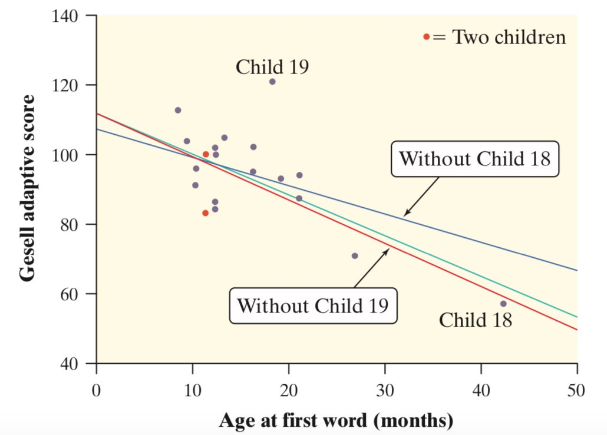
Courtesy of Starnes, Daren S. and Tabor, Josh. The Practice of Statistics—For the AP Exam, 5th Edition. Cengage Publishing.
Outliers
An outlier is a point in which the y-value is far away from the rest of the points, that is, it has a high-magnitude residual. These points heavily reduce the correlation of the scatterplot and can occasionally change the y-intercept of a regression line. Child 19 on the scatterplot above is an outlier. 😳
High-Leverage Points
A high-leverage point is a point in which the x-value is far away from the rest of the points. These points pull the regression line towards this point, and thus can significantly change the slope of the line. It can occasionally change the y-intercept of a regression line. Child 18 on the scatterplot above is a high-leverage point. 🎩
Overall, it's crucial to identify influential points in a regression model because they can have a large impact on the estimates of the model parameters and the overall fit of the model. If an influential point is an outlier, it may be appropriate to exclude it from the model because it may not be representative of the underlying pattern in the data. If an influential point is a high-leverage point, it may be worth considering whether the model is appropriate for the data or if a different model would be more suitable.
Transforming Data and Nonlinear Regression
Sometimes, a linear model is not a good fit for a set of data, and thus it is better to use a nonlinear model. The types that we have to know for this class are exponential and power regression models. (There is also polynomial regression, but that requires knowledge of linear algebra, which is beyond the scope of this course.) 💃
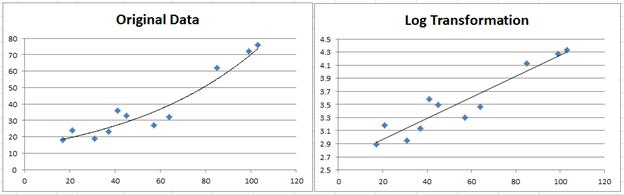
To use exponential and power regression models, it is usually necessary to transform the data to linearize it. This involves applying a function to the predictor and/or response variables in order to transform them into a form that is more suitable for linear regression. For example, the logarithmic transformation is often used to linearize exponential data, while the square root or logarithmic transformation is often used to linearize power data.
Don't worry, though! Most calculators have options to automatically calculate this for you.
Exponential Models
Exponential models have the form ŷ=ab^x, where a and b are constants and x is the explanatory variable. In order to fit an exponential model using linear regression, it is necessary to transform the data so that the relationship between the transformed response variable and the predictor variable is linear. 🚚
To do this, you can take the natural logarithm of both sides of the exponential model equation. This gives you ln(ŷ) = ln(a) + ln(b)x. The relationship between ln(ŷ) and x is now linear, so you can fit a linear regression model to the transformed data. The y-intercept of the model will be equal to ln(a), and the slope will be equal to ln(b).
This means that the relationship between ln(ŷ) and x is linear, so we find the LSRL of this transformed data with the y-intercept being a* and the slope being b*. To find a and b, we use:
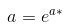
image courtesy of: codecogs.com
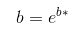
image courtesy of: codecogs.com
Power Models
Power models have the form ŷ=ax^b. Like exponential models, we also take the natural logarithm of both sides, and with manipulation, we get ln(ŷ) = ln(a) + bln(x). This time, the relationship between ln(ŷ) and ln(x) is linear. With the LSRL of the transformer data again having y-intercept a* and slope b*, we have:
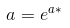
image courtesy of: codecogs.com
and b = b*.
How Can I Tell, Then?
When evaluating which transformation to use in an exponential or power regression model, it's important to consider both the residual plots of the transformed data and the R^2 value. We pick the right model by seeing whether the residuals are randomly scattered and not curved and also whether the R^2 is close to 1. 🔎
By the way, the R^2 is interpreted as the percent of variation in the response variable that can be explained by a power/exponential model relative to the explanatory variable, which is very similar to its linear counterpart. If the conditions above aren’t met, then there may be another model that may work that we haven’t learned or there are influential points skewing the data set, which is more likely!
To summarize, if our data appears to be an exponential model, we need to take the natural log (or any other base log) of our y coordinates. If our data appears to be a power model, such as a quadratic or cubic function, we need to take the log of both our x and y coordinates.
Source: Real Statistics
🎥 Watch: AP Stats - Exploring Two-Variable Data
Practice Problem
You are a statistician working for a company that manufactures and sells a certain type of light bulb. The company wants to understand how the price of the light bulbs affects the number of units sold. To do this, you collect data on the number of units sold and the price of the light bulbs for a sample of 50 different stores.
You begin by performing a linear regression on the data and find that the model has a poor fit, with a low R-squared value. You decide to try transforming the data by taking the natural logarithm of the number of units sold, and then performing a linear regression on the transformed data.
You find that the transformed data has a better fit, with a higher R-squared value. The equation of the transformed model is:
ln(units sold) = 0.5 * ln(price) + 2
You want to transform the model back to its original form so that you can make predictions in terms of the original variables. To do this, you can use the following formula:
units sold = e^(b * price^a), where a and b are constants.
Using the equation of the transformed model, find the values of a and b in the original model.
⭐ Hint: Remember that the natural logarithm of a number is the exponent to which the base e must be raised to get that number. For example, ln(2) = 0.69, because e^0.69 = 2.
Answer
First, we need to rewrite the equation of the transformed model in terms of the original variables. Since ln(units sold) is equal to 0.5 * ln(price) + 2, we can rewrite this equation as:
ln(units sold) = ln(price^0.5) + 2
Using the property of logarithms that ln(a^b) = b * ln(a), we can rewrite the equation as:
ln(units sold) = 0.5 * ln(price) + 2
Then, we can use the formula for the original model to find the values of a and b. Setting a equal to 0.5 and b equal to e^2, we get:
units sold = e^(2 * price^0.5)
Therefore, the values of a and b in the original model are a = 0.5 and b = e^2.
Key Terms to Review (17)
Correlation
: Correlation refers to the statistical measure of how two variables are related to each other. It indicates both the strength and direction of their relationship.Exponential Regression Models
: Exponential regression models are statistical models that describe the relationship between two variables using an exponential function. These models are used when the rate of change of one variable is proportional to its current value.High-leverage points
: High-leverage points are data points that have a strong influence on the regression line. These points can significantly affect the slope and position of the line.Least Squares Regression Model
: The least squares regression model is a statistical model that finds the best-fitting line through a set of data points by minimizing the sum of the squared differences between the observed and predicted values. It is used to analyze the relationship between two variables and make predictions based on that relationship.Logarithmic Transformation
: Logarithmic transformation is a mathematical technique used to transform data so that it becomes more linear. It involves taking the logarithm of each data point, which can help in fitting linear or other types of regression models.Natural Logarithm
: The natural logarithm, denoted as ln(x), is the inverse function of exponential growth. It represents the power to which the base (e) must be raised to obtain a given number (x).Nonlinear Regression
: Nonlinear regression is a statistical method used to model and analyze relationships between variables when the relationship cannot be adequately described by a linear equation. It involves fitting a curve or function to the data points in order to make predictions or understand the underlying pattern.Outliers
: Outliers are extreme values that significantly differ from other values in a dataset. They can greatly affect statistical analyses and should be carefully examined.Power Regression Models
: Power regression models are statistical models that describe the relationship between two variables using a power function. These models are used when the rate of change of one variable depends on the exponent of another variable.R^2 Value
: The R^2 value, also known as the coefficient of determination, measures how well a regression model fits the data points. It represents the proportion of variation in the dependent variable that can be explained by changes in the independent variable(s).Regression Model
: A regression model is a statistical tool used to examine the relationship between a dependent variable and one or more independent variables. It helps us understand how changes in the independent variables affect the dependent variable.residual
: A residual is the difference between an observed value and its predicted value in a regression model. It represents how much the actual data point deviates from the estimated line or curve.Residual Plots
: Residual plots are graphical representations that show differences between observed and predicted values in a regression analysis. They help identify patterns or trends in these differences and assess whether assumptions of linear regression are met.Scatterplot
: A scatterplot is a graph that displays the relationship between two quantitative variables. It uses dots to represent individual data points and shows how they are distributed along the x and y axes.Slope
: Slope represents how steep or flat a line is. In statistics, it specifically refers to how much one variable changes for every unit change in another variable.Transforming Data
: Transforming data involves applying mathematical operations to change its original form. This process helps make patterns more visible, relationships more linear, or distributions more symmetric.y-intercept
: The y-intercept is the point where a line or curve intersects the y-axis. It represents the value of the dependent variable when the independent variable is zero.2.9 Analyzing Departures from Linearity
6 min read•december 29, 2022
Athena_Codes
Jed Quiaoit
Athena_Codes
Jed Quiaoit
Sometimes, the least squares regression model may not be the best for representing a data set. We’re going to list some reasons why. While we briefly introduced them in section 2.4, we'll go into further detail here.
Influential Points
An influential point is a point that when added, significantly changes the regression model, whether by affecting the slope, y-intercept, or correlation. There are two types: outliers and high-leverage points, which are both shown in this graph. ⚒️

Courtesy of Starnes, Daren S. and Tabor, Josh. The Practice of Statistics—For the AP Exam, 5th Edition. Cengage Publishing.
Outliers
An outlier is a point in which the y-value is far away from the rest of the points, that is, it has a high-magnitude residual. These points heavily reduce the correlation of the scatterplot and can occasionally change the y-intercept of a regression line. Child 19 on the scatterplot above is an outlier. 😳
High-Leverage Points
A high-leverage point is a point in which the x-value is far away from the rest of the points. These points pull the regression line towards this point, and thus can significantly change the slope of the line. It can occasionally change the y-intercept of a regression line. Child 18 on the scatterplot above is a high-leverage point. 🎩
Overall, it's crucial to identify influential points in a regression model because they can have a large impact on the estimates of the model parameters and the overall fit of the model. If an influential point is an outlier, it may be appropriate to exclude it from the model because it may not be representative of the underlying pattern in the data. If an influential point is a high-leverage point, it may be worth considering whether the model is appropriate for the data or if a different model would be more suitable.
Transforming Data and Nonlinear Regression
Sometimes, a linear model is not a good fit for a set of data, and thus it is better to use a nonlinear model. The types that we have to know for this class are exponential and power regression models. (There is also polynomial regression, but that requires knowledge of linear algebra, which is beyond the scope of this course.) 💃
To use exponential and power regression models, it is usually necessary to transform the data to linearize it. This involves applying a function to the predictor and/or response variables in order to transform them into a form that is more suitable for linear regression. For example, the logarithmic transformation is often used to linearize exponential data, while the square root or logarithmic transformation is often used to linearize power data.
Don't worry, though! Most calculators have options to automatically calculate this for you.
Exponential Models
Exponential models have the form ŷ=ab^x, where a and b are constants and x is the explanatory variable. In order to fit an exponential model using linear regression, it is necessary to transform the data so that the relationship between the transformed response variable and the predictor variable is linear. 🚚
To do this, you can take the natural logarithm of both sides of the exponential model equation. This gives you ln(ŷ) = ln(a) + ln(b)x. The relationship between ln(ŷ) and x is now linear, so you can fit a linear regression model to the transformed data. The y-intercept of the model will be equal to ln(a), and the slope will be equal to ln(b).
This means that the relationship between ln(ŷ) and x is linear, so we find the LSRL of this transformed data with the y-intercept being a* and the slope being b*. To find a and b, we use:
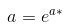
image courtesy of: codecogs.com
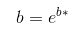
image courtesy of: codecogs.com
Power Models
Power models have the form ŷ=ax^b. Like exponential models, we also take the natural logarithm of both sides, and with manipulation, we get ln(ŷ) = ln(a) + bln(x). This time, the relationship between ln(ŷ) and ln(x) is linear. With the LSRL of the transformer data again having y-intercept a* and slope b*, we have:
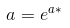
image courtesy of: codecogs.com
and b = b*.
How Can I Tell, Then?
When evaluating which transformation to use in an exponential or power regression model, it's important to consider both the residual plots of the transformed data and the R^2 value. We pick the right model by seeing whether the residuals are randomly scattered and not curved and also whether the R^2 is close to 1. 🔎
By the way, the R^2 is interpreted as the percent of variation in the response variable that can be explained by a power/exponential model relative to the explanatory variable, which is very similar to its linear counterpart. If the conditions above aren’t met, then there may be another model that may work that we haven’t learned or there are influential points skewing the data set, which is more likely!
To summarize, if our data appears to be an exponential model, we need to take the natural log (or any other base log) of our y coordinates. If our data appears to be a power model, such as a quadratic or cubic function, we need to take the log of both our x and y coordinates.

Source: Real Statistics
🎥 Watch: AP Stats - Exploring Two-Variable Data
Practice Problem
You are a statistician working for a company that manufactures and sells a certain type of light bulb. The company wants to understand how the price of the light bulbs affects the number of units sold. To do this, you collect data on the number of units sold and the price of the light bulbs for a sample of 50 different stores.
You begin by performing a linear regression on the data and find that the model has a poor fit, with a low R-squared value. You decide to try transforming the data by taking the natural logarithm of the number of units sold, and then performing a linear regression on the transformed data.
You find that the transformed data has a better fit, with a higher R-squared value. The equation of the transformed model is:
ln(units sold) = 0.5 * ln(price) + 2
You want to transform the model back to its original form so that you can make predictions in terms of the original variables. To do this, you can use the following formula:
units sold = e^(b * price^a), where a and b are constants.
Using the equation of the transformed model, find the values of a and b in the original model.
⭐ Hint: Remember that the natural logarithm of a number is the exponent to which the base e must be raised to get that number. For example, ln(2) = 0.69, because e^0.69 = 2.
Answer
First, we need to rewrite the equation of the transformed model in terms of the original variables. Since ln(units sold) is equal to 0.5 * ln(price) + 2, we can rewrite this equation as:
ln(units sold) = ln(price^0.5) + 2
Using the property of logarithms that ln(a^b) = b * ln(a), we can rewrite the equation as:
ln(units sold) = 0.5 * ln(price) + 2
Then, we can use the formula for the original model to find the values of a and b. Setting a equal to 0.5 and b equal to e^2, we get:
units sold = e^(2 * price^0.5)
Therefore, the values of a and b in the original model are a = 0.5 and b = e^2.
Key Terms to Review (17)
Correlation
: Correlation refers to the statistical measure of how two variables are related to each other. It indicates both the strength and direction of their relationship.Exponential Regression Models
: Exponential regression models are statistical models that describe the relationship between two variables using an exponential function. These models are used when the rate of change of one variable is proportional to its current value.High-leverage points
: High-leverage points are data points that have a strong influence on the regression line. These points can significantly affect the slope and position of the line.Least Squares Regression Model
: The least squares regression model is a statistical model that finds the best-fitting line through a set of data points by minimizing the sum of the squared differences between the observed and predicted values. It is used to analyze the relationship between two variables and make predictions based on that relationship.Logarithmic Transformation
: Logarithmic transformation is a mathematical technique used to transform data so that it becomes more linear. It involves taking the logarithm of each data point, which can help in fitting linear or other types of regression models.Natural Logarithm
: The natural logarithm, denoted as ln(x), is the inverse function of exponential growth. It represents the power to which the base (e) must be raised to obtain a given number (x).Nonlinear Regression
: Nonlinear regression is a statistical method used to model and analyze relationships between variables when the relationship cannot be adequately described by a linear equation. It involves fitting a curve or function to the data points in order to make predictions or understand the underlying pattern.Outliers
: Outliers are extreme values that significantly differ from other values in a dataset. They can greatly affect statistical analyses and should be carefully examined.Power Regression Models
: Power regression models are statistical models that describe the relationship between two variables using a power function. These models are used when the rate of change of one variable depends on the exponent of another variable.R^2 Value
: The R^2 value, also known as the coefficient of determination, measures how well a regression model fits the data points. It represents the proportion of variation in the dependent variable that can be explained by changes in the independent variable(s).Regression Model
: A regression model is a statistical tool used to examine the relationship between a dependent variable and one or more independent variables. It helps us understand how changes in the independent variables affect the dependent variable.residual
: A residual is the difference between an observed value and its predicted value in a regression model. It represents how much the actual data point deviates from the estimated line or curve.Residual Plots
: Residual plots are graphical representations that show differences between observed and predicted values in a regression analysis. They help identify patterns or trends in these differences and assess whether assumptions of linear regression are met.Scatterplot
: A scatterplot is a graph that displays the relationship between two quantitative variables. It uses dots to represent individual data points and shows how they are distributed along the x and y axes.Slope
: Slope represents how steep or flat a line is. In statistics, it specifically refers to how much one variable changes for every unit change in another variable.Transforming Data
: Transforming data involves applying mathematical operations to change its original form. This process helps make patterns more visible, relationships more linear, or distributions more symmetric.y-intercept
: The y-intercept is the point where a line or curve intersects the y-axis. It represents the value of the dependent variable when the independent variable is zero.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.