9.5 Additional Information and Full Hypothesis Test Examples

Hypothesis testing is a crucial statistical method for making decisions about populations based on sample data. It involves setting up hypotheses, calculating test statistics, and interpreting p-values to draw conclusions about the validity of claims.

The process includes formulating null and alternative hypotheses, determining significance levels, and calculating test statistics. By comparing p-values to predetermined thresholds, researchers can make informed decisions about rejecting or failing to reject null hypotheses, guiding further actions or investigations.

Hypothesis Testing Concepts

more resources to help you study

practice questions

Significance and p-value interpretation

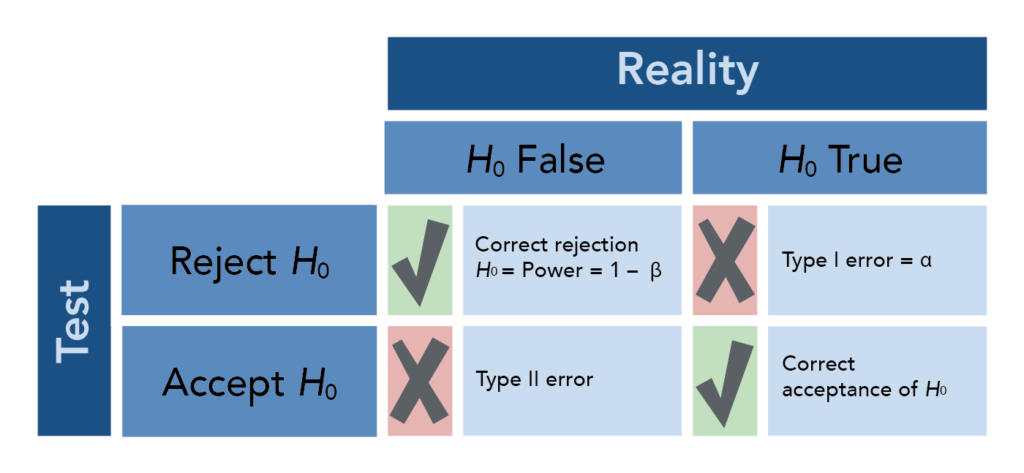
• Level of significance ($\alpha$) represents the maximum acceptable risk of rejecting the null hypothesis ($H_0$) when it is actually true (Type I error)
  • Commonly set at 0.01, 0.05, or 0.10 and determined before conducting the test
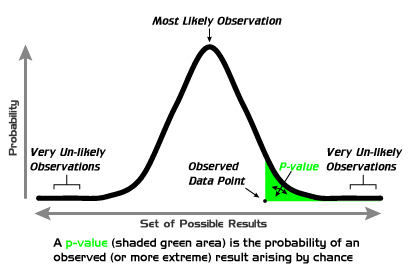
• p-value quantifies the probability of obtaining a test statistic as extreme as or more extreme than the observed value, assuming $H_0$ is true
  • Calculated from sample data and compared to $\alpha$ to make a decision
    • Reject $H_0$ if p-value ≤ $\alpha$ (statistically significant)
    • Fail to reject $H_0$ if p-value > $\alpha$ (not statistically significant)
• Role in decision-making: $\alpha$ sets the threshold for rejecting $H_0$, while p-value provides evidence against $H_0$
  • Smaller p-values indicate stronger evidence against $H_0$ (0.001 vs 0.04)
• Statistical power is the probability of correctly rejecting $H_0$ when it is false, which increases with larger effect sizes

Types of hypothesis tests

• Alternative hypothesis ($H_a$ or $H_1$) determines the test type based on the parameter and value
  • Left-tailed: $H_a: \text{parameter} < \text{value}$ with critical region in left tail ($H_a: \mu < 100$)
  • Right-tailed: $H_a: \text{parameter} > \text{value}$ with critical region in right tail ($H_a: p > 0.5$)
  • Two-tailed: $H_a: \text{parameter} \neq \text{value}$ with critical region split between left and right tails ($H_a: \mu \neq 50$)
• Critical value(s) depend on test type and $\alpha$
  • Left-tailed: Lower critical value
  • Right-tailed: Upper critical value
  • Two-tailed: Lower and upper critical values ($-z_{\alpha/2}$ and $z_{\alpha/2}$ for z-test)

Test Planning and Interpretation

• Confidence interval provides a range of plausible values for the population parameter, complementing hypothesis test results
• Effect size quantifies the magnitude of the difference between groups or the strength of a relationship
• Sample size determination is crucial for achieving desired statistical power and precision in hypothesis testing

Full Hypothesis Test Example

Single population proportion test

1. Formulate null and alternative hypotheses

   • $H_0: p = p_0$ ($p_0$ is claimed proportion)
   • $H_a: p < p_0$, $p > p_0$, or $p \neq p_0$ based on context

2. Determine significance level ($\alpha$)

3. Calculate test statistic ($z$) using sample proportion ($\hat{p}$)

   • $z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$ ($n$ is sample size)

4. Find p-value based on test statistic and test type using standard normal distribution

5. Compare p-value to $\alpha$

   • Reject $H_0$ if p-value ≤ $\alpha$
   • Fail to reject $H_0$ if p-value > $\alpha$

6. Interpret results in problem context

   • State if there is sufficient evidence to support $H_a$
   • Discuss practical implications of findings (election outcome, product defect rate)