11.4 De Broglie wavelength

Wave-Particle Duality Concept

Wave-particle duality is one of the central ideas in quantum mechanics. It says that matter and light both exhibit wave-like and particle-like properties, depending on how you observe them. This directly challenges classical physics, which treats particles and waves as completely separate things.

Matter Waves Introduction

In 1924, Louis de Broglie proposed that all matter possesses wave-like characteristics, not just light. The wavelength of these "matter waves" is inversely proportional to the particle's momentum. This single idea explains phenomena like electron diffraction and interference patterns that classical mechanics simply can't account for.

The key distinction:

• Classical mechanics treats objects purely as particles with definite positions and trajectories
• Quantum mechanics introduces wave-like behavior, where particles can interfere and diffract just like light waves

De Broglie Hypothesis

De Broglie's reasoning was elegant: if light (which everyone thought was a wave) can behave like a particle (photons), then why can't particles behave like waves? He extended wave-particle duality to all matter by assigning a wavelength to every particle that has momentum.

A critical prediction falls out of this: wave nature becomes more apparent for smaller, lighter particles. That's because lighter particles have less momentum at a given speed, which means a longer wavelength. This hypothesis led directly to the development of wave mechanics and eventually the Schrödinger equation.

De Broglie Wavelength Equation

The De Broglie wavelength equation is the quantitative heart of this topic. It connects a particle property (momentum) to a wave property (wavelength), giving you a way to calculate exactly how "wave-like" a given particle is.

Derivation of the Formula

The derivation combines three well-known equations:

1. Start with Einstein's energy-mass equivalence: $E = mc^2$
2. Set this equal to Planck's equation for photon energy: $E = hf$
3. Use the wave equation $c = \lambda f$ to substitute $f = c/\lambda$
4. This gives $mc^2 = hc/\lambda$, which simplifies to $\lambda = h/(mc)$
5. Recognizing that $mc$ is just the momentum $p$ of a photon, generalize to any particle:

$\lambda = \frac{h}{p}$

Where:

• $\lambda$ = wavelength of the particle
• $h$ = Planck's constant ($6.626 \times 10^{-34}$ J·s)
• $p$ = momentum of the particle ($p = mv$ for non-relativistic speeds)

Units and Dimensions

• Wavelength ($\lambda$): meters (m)
• Planck's constant ($h$): joule-seconds (J·s)
• Momentum ($p$): kg·m/s

Dimensional analysis confirms the equation works out: $[\lambda] = \frac{J \cdot s}{kg \cdot m/s} = \frac{kg \cdot m^2/s}{kg \cdot m/s} = m$

Typical De Broglie wavelengths give you a sense of scale:

• Electrons: on the order of picometers ($10^{-12}$ m), comparable to atomic spacing
• Protons: femtometers ($10^{-15}$ m), comparable to nuclear dimensions

Relationship to Momentum

The inverse relationship between wavelength and momentum is the single most important thing to internalize about this equation. Everything else follows from it.

Momentum and Wavelength Correlation

Since $\lambda = h/p$, increasing momentum means decreasing wavelength, and vice versa. This has direct physical consequences:

• High-momentum particles have very short wavelengths, so they behave more like classical particles
• Low-momentum particles have longer wavelengths, so wave effects become noticeable
• At the same speed, an electron (small mass, small momentum) has a much longer wavelength than a proton (larger mass, larger momentum)
• Macroscopic objects have wavelengths so absurdly tiny that wave behavior is completely undetectable

Particle vs. Wave Behavior

Whether something "acts like a wave" or "acts like a particle" depends on how its De Broglie wavelength compares to the relevant length scales in the problem:

• Wavelength comparable to atomic dimensions (~0.1 nm): wave behavior dominates. You'll see diffraction and interference.
• Wavelength much smaller than the object or apparatus: particle behavior prevails. Classical mechanics works fine.

This is exactly why quantum mechanics matters for electrons in atoms but not for baseballs. It's not that baseballs don't have a wavelength; it's that their wavelength is so small it has zero observable effect.

Applications of De Broglie Wavelength

Electron Microscopy

Electron microscopes exploit the fact that accelerated electrons have wavelengths far shorter than visible light (which bottoms out around 400 nm). Because resolution is limited by wavelength, electron microscopes can image structures at the atomic scale, with resolution down to about 50 pm.

Two main types:

• Transmission Electron Microscope (TEM): electrons pass through a thin sample
• Scanning Electron Microscope (SEM): electrons scan across a surface to build a 3D image

These are used extensively in materials science, biology, and nanotechnology.

Neutron Diffraction

Thermal neutrons from a nuclear reactor have De Broglie wavelengths around 0.1–0.2 nm, which is perfect for probing crystal structures. Neutrons offer advantages over X-rays in certain situations:

• They penetrate deeper into materials than X-rays or electrons
• They're especially sensitive to light atoms like hydrogen
• They can reveal magnetic structure because neutrons have a magnetic moment

Applications include studying magnetic materials, biological molecules, and hydrogen-containing compounds.

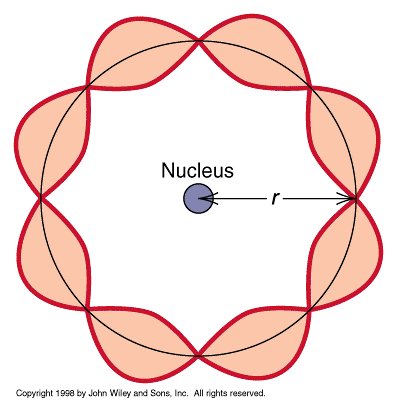
Experimental Evidence

Davisson-Germer Experiment

This 1927 experiment provided the first direct confirmation of De Broglie's hypothesis. Here's what happened:

1. Clinton Davisson and Lester Germer fired a beam of electrons at a nickel crystal
2. The electrons scattered off the crystal surface
3. The scattered electrons produced an interference pattern, just like X-rays diffracting off a crystal
4. The measured wavelength of the electrons matched De Broglie's prediction ($\lambda = h/p$)

This was decisive proof that particles have wave properties. Davisson shared the 1937 Nobel Prize in Physics for this work.

Electron Diffraction Patterns

When electrons pass through or reflect off crystalline materials, they produce diffraction patterns nearly identical to those from X-rays. The intensity and spacing of the diffracted beams depend on the crystal structure, making electron diffraction a powerful tool for studying:

• Crystal structures and atomic arrangements
• Surface properties of solids

Common techniques include Low-Energy Electron Diffraction (LEED) and Reflection High-Energy Electron Diffraction (RHEED).

Quantum Mechanical Implications

Uncertainty Principle Connection

The wave nature of particles is directly tied to Heisenberg's uncertainty principle. If a particle is a wave, it doesn't have a single precise position. Trying to pin down its location more precisely means you lose information about its momentum, and vice versa.

This is expressed mathematically as:

$\Delta x \, \Delta p \geq \frac{\hbar}{2}$

where $\hbar = h/(2\pi)$ is the reduced Planck's constant. This isn't a limitation of our instruments. It's a fundamental property of nature that emerges because particles have wave-like behavior.

Wave Function Interpretation

De Broglie's matter waves were eventually interpreted as probability waves, described by Schrödinger's wave equation. The wave function $\psi$ represents the quantum state of a particle, and $|\psi|^2$ gives the probability density of finding the particle at a specific location.

This framework explains:

• Quantum tunneling: particles can pass through barriers they classically shouldn't be able to cross
• Discrete energy levels: electrons in atoms can only occupy certain allowed energies
• Electron orbitals: the shapes of regions where electrons are likely to be found

De Broglie Wavelength Calculations

Working through actual numbers makes the physics concrete. Notice how dramatically wavelength changes between macroscopic and subatomic scales.

For Macroscopic Objects

• Baseball (mass 0.145 kg, velocity ~40 m/s): $\lambda \approx 1.1 \times 10^{-34}$ m. That's roughly $10^{-19}$ times smaller than a proton. Completely undetectable.
• Walking human (mass 70 kg, velocity 1 m/s): $\lambda \approx 9.5 \times 10^{-36}$ m. Even smaller.

This is why you never notice your own wave nature.

For Subatomic Particles

• Electron in a hydrogen atom (ground state): $\lambda \approx 0.33$ nm, which is comparable to the atomic radius. Wave behavior dominates at this scale.
• Thermal neutron (from a nuclear reactor): $\lambda \approx 0.18$ nm, making neutrons ideal for diffraction experiments with crystals.
• Proton in the Large Hadron Collider (near the speed of light): $\lambda \approx 1.3 \times 10^{-19}$ m, small enough to probe the internal structure of other protons.

Limitations and Considerations

Classical vs. Quantum Regimes

The De Broglie wavelength tells you which regime you're in:

• Classical regime: $\lambda$ is much smaller than the object or any relevant length scale. Use Newton's laws.
• Quantum regime: $\lambda$ is comparable to or larger than the relevant length scale. You need quantum mechanics.
• Transition region: both behaviors can matter, and the physics gets complicated.

The factors that push you toward the quantum regime are small mass, low velocity, and isolation from environmental interactions. Larger objects interacting with their environment undergo decoherence, which destroys wave-like behavior very quickly.

Wavelength Threshold for Observation

To actually observe De Broglie waves, the wavelength needs to be comparable to the resolution of your measurement apparatus:

• Optical microscopes: ~200 nm
• X-ray diffraction: ~0.1 nm
• Electron microscopes: ~50 pm

A major practical challenge is maintaining quantum coherence. Environmental interactions (thermal vibrations, stray electromagnetic fields) can destroy the wave-like behavior of particles. This is why quantum experiments often require extremely low temperatures and careful isolation, and why observing quantum behavior in larger objects remains an active area of research.