8.1 DFT Definition and Properties

The Discrete Fourier Transform (DFT) converts a finite sequence of samples into a set of complex coefficients that reveal the frequency content of that signal. It's the foundational tool for moving between time-domain and frequency-domain representations in digital signal processing, and nearly every spectral analysis technique you'll encounter builds on it.

Discrete Fourier Transform

Definition and Formulas

The DFT takes $N$ equally-spaced samples of a signal and maps them to $N$ complex coefficients, each corresponding to a specific frequency component. Think of it as decomposing your signal into a sum of complex sinusoids at discrete frequencies.

Forward DFT:

$X[k] = \sum_{n=0}^{N-1} x[n] \, e^{-j 2\pi k n / N}, \quad k = 0, 1, \dots, N-1$

• $x[n]$ is the input sequence (time-domain samples)
• $X[k]$ is the output sequence (frequency-domain coefficients)
• $N$ is the total number of samples
• $k$ is the frequency index

Inverse DFT (IDFT):

$x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \, e^{j 2\pi k n / N}, \quad n = 0, 1, \dots, N-1$

The IDFT reconstructs the original time-domain sequence from the frequency-domain coefficients. Notice the only differences from the forward DFT: the sign in the exponent flips from negative to positive, and there's a $\frac{1}{N}$ scaling factor out front.

A useful shorthand is the twiddle factor $W_N = e^{-j 2\pi / N}$, which lets you write the DFT compactly as $X[k] = \sum_{n=0}^{N-1} x[n] \, W_N^{kn}$. You'll see this notation frequently when studying FFT algorithms.

Core Properties at a Glance

Three properties define how the DFT behaves:

• Linearity: The DFT is a linear transformation. The DFT of a weighted sum of sequences equals the same weighted sum of their individual DFTs.
• Periodicity: Both $X[k]$ and $x[n]$ are periodic with period $N$, meaning $X[k+N] = X[k]$ and $x[n+N] = x[n]$. This is inherent to the DFT's structure, not a property of your actual signal.
• Conjugate Symmetry (for real-valued inputs): If $x[n]$ is real, then $X[N-k] = X^*[k]$, where $^*$ denotes complex conjugation. This means the second half of the DFT output mirrors the first half, so you only need to look at indices $k = 0$ through $N/2$ for unique frequency information.

DFT Properties

Linearity

Linearity has two parts:

• Additivity: If $x_1[n] \xrightarrow{\text{DFT}} X_1[k]$ and $x_2[n] \xrightarrow{\text{DFT}} X_2[k]$, then $x_1[n] + x_2[n] \xrightarrow{\text{DFT}} X_1[k] + X_2[k]$.
• Scaling: For any constant $a$, the signal $a \cdot x[n] \xrightarrow{\text{DFT}} a \cdot X[k]$.

This is straightforward but powerful: you can analyze complex signals by breaking them into simpler components, transforming each one separately, and adding the results.

Periodicity

The DFT treats your $N$-point sequence as though it repeats forever in both directions. This implicit periodicity means $X[k + N] = X[k]$ for all $k$, and $x[n + N] = x[n]$ for all $n$.

Why does this matter? It means that when you perform operations like convolution using the DFT, you get circular convolution, not the linear convolution you might expect. If you need linear convolution results, you'll have to zero-pad your sequences appropriately.

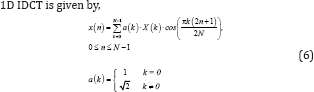
Symmetry (Real-Valued Signals)

For real-valued input sequences, conjugate symmetry gives you specific structure in the DFT output:

• Real part: $\text{Re}\{X[k]\} = \text{Re}\{X[N-k]\}$ (even symmetric)
• Imaginary part: $\text{Im}\{X[k]\} = -\text{Im}\{X[N-k]\}$ (odd symmetric)
• Magnitude: $|X[k]| = |X[N-k]|$ (even symmetric)
• Phase: $\angle X[k] = -\angle X[N-k]$ (odd symmetric)

This redundancy is why you only see frequency plots up to $N/2$ (the Nyquist index) for real signals.

Parseval's Theorem

Parseval's theorem states that the total energy of a signal is the same whether you compute it in the time domain or the frequency domain:

$\sum_{n=0}^{N-1} |x[n]|^2 = \frac{1}{N} \sum_{k=0}^{N-1} |X[k]|^2$

This gives you a useful sanity check: if your DFT result doesn't preserve energy (accounting for the $\frac{1}{N}$ factor), something went wrong in your computation.

Convolution Theorem

The convolution theorem is one of the most practically important DFT properties. It connects two operations:

• Circular convolution in time ↔ Pointwise multiplication in frequency: If $y[n] = x_1[n] \circledast x_2[n]$, then $Y[k] = X_1[k] \cdot X_2[k]$.
• Multiplication in time ↔ Circular convolution in frequency (scaled by $\frac{1}{N}$).

This is why filtering is so often done in the frequency domain. Instead of computing an expensive convolution directly, you can:

1. Take the DFT of both sequences
2. Multiply the results element-by-element
3. Take the IDFT of the product

For long sequences, this approach (combined with the FFT) is dramatically faster than direct convolution.

DFT and Fourier Series

Relationship between DFT and Fourier Series

The continuous-time Fourier Series represents a periodic function $x(t)$ with period $T$ as a sum of complex exponentials, with coefficients:

$c_k = \frac{1}{T} \int_0^T x(t) \, e^{-j 2\pi k t / T} \, dt$

The DFT can be understood as a sampled, finite-length version of this. If you sample $x(t)$ at $N$ equally-spaced points within one period, the DFT coefficients $X[k]$ are proportional to the Fourier Series coefficients $c_k$ at the discrete frequencies $\omega_k = 2\pi k / N$.

Convergence and Periodicity

As $N \to \infty$ (more and more samples per period), the DFT coefficients converge to the Fourier Series coefficients. Both the DFT and the Fourier Series share the assumption that the signal is periodic. The difference is that the DFT works with a finite number of samples and produces a finite number of frequency coefficients, making it computable on real hardware.

Frequency Spectrum Analysis with DFT

Computing the Frequency Spectrum

The DFT output $X[k]$ is complex-valued, so it encodes two pieces of information at each frequency index $k$:

• Magnitude spectrum $|X[k]|$: the amplitude of the frequency component at index $k$. This tells you how much of that frequency is present.
• Phase spectrum $\angle X[k]$: the phase offset of that component. This tells you where in its cycle that frequency component starts.

Together, the magnitude and phase spectra fully describe the frequency content of your signal.

Frequency Resolution and Spectral Leakage

Frequency resolution is the smallest frequency difference the DFT can distinguish:

$\Delta f = \frac{f_s}{N}$

where $f_s$ is the sampling frequency and $N$ is the number of samples. To improve resolution, you either increase $N$ (collect more samples) or decrease $f_s$ (sample more slowly, though this limits your maximum detectable frequency).

Spectral leakage occurs when the signal's true frequency doesn't land exactly on one of the DFT's discrete frequency bins (integer multiples of $\Delta f$). Because the DFT assumes your $N$-point window repeats periodically, any discontinuity at the window boundaries causes energy to "leak" into adjacent frequency bins, smearing the spectrum.

To reduce spectral leakage, apply a window function to the signal before computing the DFT. Common choices include:

• Hann window: Good general-purpose choice with decent frequency resolution and sidelobe suppression
• Hamming window: Similar to Hann but with slightly lower sidelobes at the cost of wider main lobe

Windowing always involves a tradeoff: better sidelobe suppression comes at the expense of a wider main lobe (reduced frequency resolution).

Fast Fourier Transform (FFT)

The FFT isn't a different transform; it's an efficient algorithm for computing the exact same DFT. The direct DFT computation requires $O(N^2)$ complex multiplications, which becomes prohibitively slow for large $N$. The FFT reduces this to $O(N \log N)$ by exploiting the symmetry and periodicity of the twiddle factors.

The most common FFT algorithm is the Cooley-Tukey algorithm, which uses a divide-and-conquer strategy:

1. Split the $N$-point DFT into two $N/2$-point DFTs (one for even-indexed samples, one for odd-indexed samples)
2. Compute each smaller DFT recursively
3. Combine the results using twiddle factor multiplications ("butterfly operations")

This recursive splitting is why the Cooley-Tukey FFT works most efficiently when $N$ is a power of 2 (called a radix-2 FFT). Other variants like the Prime-Factor algorithm handle cases where $N$ has mixed prime factors.