🎲intro to probability review
14.3 Applications of the central limit theorem
Last Updated on July 30, 2024
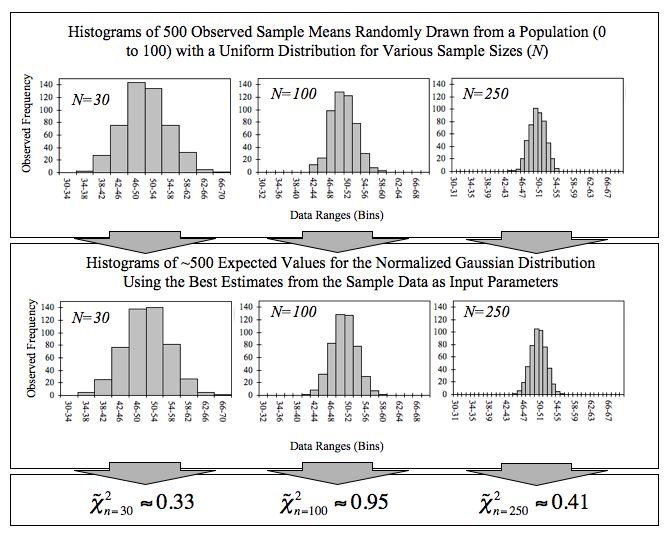
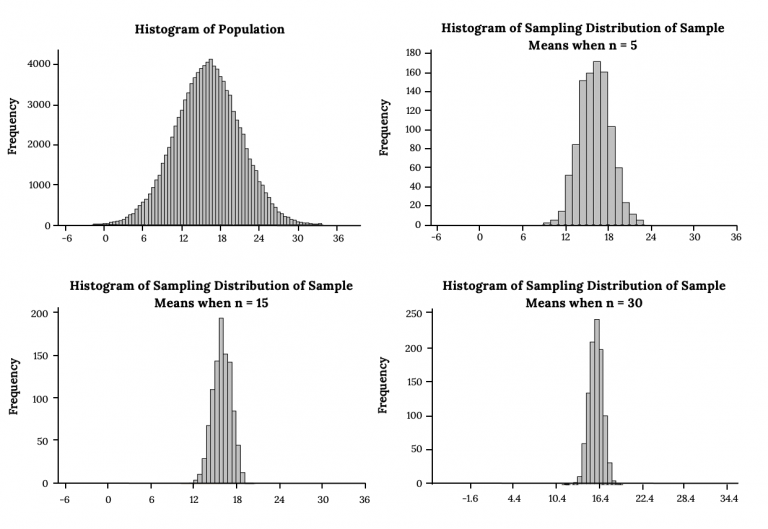
The Central Limit Theorem (CLT) is a game-changer in probability. It tells us that as sample sizes grow, the distribution of sample means gets closer to normal, no matter what the original population looks like. This opens up a world of statistical tools.
CLT lets us estimate probabilities, build confidence intervals, and run hypothesis tests, even when we're dealing with non-normal data. It's the backbone of many statistical methods, making it easier to draw conclusions about populations from sample data.
Approximating Probabilities with CLT
Fundamentals of CLT
Top images from around the web for Fundamentals of CLT
6.2 The Sampling Distribution of the Sample Mean (σ Known) – Significant Statistics View original
Is this image relevant?
The Central Limit Theorem for Sample Means (Averages) | Introduction to Statistics – Gravina View original
Is this image relevant?
Teorema del límite central - Central limit theorem - xcv.wiki View original
Is this image relevant?
6.2 The Sampling Distribution of the Sample Mean (σ Known) – Significant Statistics View original
Is this image relevant?
The Central Limit Theorem for Sample Means (Averages) | Introduction to Statistics – Gravina View original
Is this image relevant?
1 of 3
Top images from around the web for Fundamentals of CLT
6.2 The Sampling Distribution of the Sample Mean (σ Known) – Significant Statistics View original
Is this image relevant?
The Central Limit Theorem for Sample Means (Averages) | Introduction to Statistics – Gravina View original
Is this image relevant?
Teorema del límite central - Central limit theorem - xcv.wiki View original
Is this image relevant?
6.2 The Sampling Distribution of the Sample Mean (σ Known) – Significant Statistics View original
Is this image relevant?
The Central Limit Theorem for Sample Means (Averages) | Introduction to Statistics – Gravina View original
Is this image relevant?
1 of 3
- Distribution of sample means approaches normal distribution as sample size increases, regardless of underlying population distribution
- For large sample sizes (n ≥ 30), sampling distribution of mean approximates normal with mean μ and standard error σ/√n
- Z-score formula for sample means calculates as
- x̄ represents sample mean
- μ represents population mean
- σ represents population standard deviation
- n represents sample size
- CLT enables normal probability calculations even for non-normally distributed populations (uniform distribution, exponential distribution)
Probability Calculations
- Standard normal distribution table or z-score calculations determine probabilities related to sample means
- When population standard deviation is unknown, sample standard deviation (s) estimates it
- Results in t-distribution usage instead of z-distribution
- Examples of probability calculations:
- Probability of sample mean falling within specific range
- Probability of sample mean exceeding certain value
Confidence Intervals with CLT
Constructing Confidence Intervals
- Confidence interval formula for population mean:
- Critical value depends on chosen confidence level (90%, 95%, 99%)
- For large samples (n ≥ 30), critical value obtained from standard normal distribution (z-distribution)
- Margin of error calculates as product of critical value and standard error
- Width of confidence interval influenced by:
- Sample size (larger sample, narrower interval)
- Population variability (higher variability, wider interval)
- Desired level of confidence (higher confidence, wider interval)
Interpretation and Application
- Confidence interval provides range of plausible values for population mean, not definitive single value
- CLT ensures approximately valid confidence intervals for large samples, even with non-normal population distributions
- Examples of confidence interval applications:
- Estimating average height of population based on sample
- Determining range of possible mean test scores for entire school
Hypothesis Testing with CLT
Fundamentals of Hypothesis Testing
- Hypothesis testing compares sample statistic to hypothesized population parameter for population inferences
- Null hypothesis (H₀) assumes no effect or difference
- Alternative hypothesis (H₁) suggests significant effect or difference
- Test statistic for means calculates using formula:
- μ₀ represents hypothesized population mean
- CLT allows z-tests or t-tests for means with large samples, even for non-normal population distributions
Testing Approaches and Considerations
- P-value approach compares calculated p-value to predetermined significance level (α) for null hypothesis decision
- Critical value approach compares calculated test statistic to critical value(s) determined by:
- Significance level
- Type of test (one-tailed or two-tailed)
- Important considerations in hypothesis testing:
- Type I errors (rejecting true null hypothesis)
- Type II errors (failing to reject false null hypothesis)
- Examples of hypothesis tests:
- Testing if average weight of product differs from advertised weight
- Determining if new teaching method improves test scores
Limitations of CLT
Assumptions and Sample Size Considerations
- CLT assumes independent and identically distributed random variables
- May not hold in real-world scenarios (time series data, clustered data)
- Small sample sizes (n < 30) may not provide sufficiently normal sampling distribution
- Especially problematic for highly skewed populations (exponential distribution, Pareto distribution)
- Larger sample sizes required for CLT effectiveness with extreme outliers or heavy-tailed distributions (Cauchy distribution)
- CLT does not guarantee normality for individual samples, only for sampling distribution of means across many samples
Scope and Alternative Methods
- CLT primarily concerns sampling distribution of means and sums
- Does not apply to all types of statistics (medians, ranges)
- For proportions or counts, CLT application differs or alternative methods more appropriate
- Binomial distribution for proportions
- Poisson distribution for counts
- Examples of CLT limitations:
- Small sample inference for highly skewed financial data
- Analysis of rare events with limited observations
Key Terms to Review (27)
Large sample size: A large sample size refers to a statistical sample that contains a sufficiently high number of observations or data points, allowing for more reliable and accurate conclusions to be drawn from the data. When a sample size is large, the results tend to better reflect the population characteristics, reducing the margin of error and increasing the power of statistical tests. This is particularly relevant in the context of probability and the central limit theorem, where larger samples lead to a normal distribution of sample means, regardless of the original distribution of the population.
Critical Value: A critical value is a point on a statistical distribution that helps determine the threshold for rejecting or failing to reject the null hypothesis in hypothesis testing. It is directly tied to the significance level, which indicates the probability of making a Type I error. The critical value is essential for applications involving confidence intervals and determining statistical significance based on the central limit theorem.
Z-distribution: The z-distribution, also known as the standard normal distribution, is a special case of the normal distribution where the mean is 0 and the standard deviation is 1. This distribution is crucial for statistical analysis, as it allows for the comparison of different datasets by standardizing scores, making it easier to calculate probabilities and critical values when applying the central limit theorem.
Asymptotic normality: Asymptotic normality refers to the property of a sequence of random variables that, as the sample size increases, the distribution of the standardized sample mean approaches a normal distribution. This concept is fundamentally connected to the Central Limit Theorem, which asserts that, given a sufficiently large sample size, the sampling distribution of the sample mean will be approximately normally distributed regardless of the shape of the population distribution, as long as the population has a finite mean and variance.
Finite Population Correction: The finite population correction (FPC) is a factor used in statistical calculations to adjust for the reduction in variance when sampling from a finite population as opposed to an infinite one. This correction becomes significant when the sample size is a large fraction of the total population size, which can lead to bias in estimates if not accounted for. The FPC helps provide more accurate estimates of population parameters, particularly when applying the central limit theorem in scenarios involving finite populations.
Non-normal population distribution: A non-normal population distribution refers to a distribution of data that does not follow the bell-shaped curve typical of a normal distribution, meaning it can be skewed or exhibit kurtosis. These distributions can have different shapes, such as uniform, bimodal, or heavily skewed, which can affect how sample means behave when applying statistical methods. Understanding non-normal distributions is crucial when considering the implications for the central limit theorem, as it influences the behavior of sample means and variances derived from such populations.
Sample proportions: Sample proportions refer to the ratio of a specific outcome within a sample relative to the total size of that sample, expressed as a fraction or percentage. This concept is crucial in understanding how sample data can be used to estimate population parameters, particularly when considering the distribution of sample proportions in relation to the central limit theorem. As sample sizes increase, the distribution of sample proportions approaches a normal distribution, which plays a significant role in hypothesis testing and confidence interval estimation.
Confidence Interval: A confidence interval is a range of values derived from sample data that is likely to contain the true population parameter with a specified level of confidence, usually expressed as a percentage. This concept is essential for understanding the reliability of estimates made from sample data, highlighting the uncertainty inherent in statistical inference. Confidence intervals provide a way to quantify the precision of sample estimates and are crucial for making informed decisions based on statistical analyses.
Random Sampling: Random sampling is a technique used to select a subset of individuals from a larger population in such a way that each individual has an equal chance of being chosen. This method is crucial because it helps ensure that the sample represents the population well, allowing for more accurate statistical inferences. By minimizing bias and ensuring randomness, random sampling plays an important role in understanding relationships between variables, especially when considering independent events and applying the central limit theorem.
Margin of error: The margin of error is a statistic that expresses the amount of random sampling error in a survey's results. It indicates the range within which the true population parameter is likely to fall, providing a measure of the uncertainty associated with an estimate. A smaller margin of error suggests greater confidence in the accuracy of the results, while a larger margin indicates more variability and less certainty.
T-distribution: The t-distribution is a probability distribution that is symmetrical and bell-shaped, similar to the normal distribution, but has heavier tails. It is particularly useful when dealing with small sample sizes or when the population standard deviation is unknown, making it essential for constructing confidence intervals and conducting hypothesis tests.
P-value: A p-value is a statistical measure that helps determine the significance of results obtained in hypothesis testing. It indicates the probability of observing data as extreme as, or more extreme than, the actual data, assuming that the null hypothesis is true. The p-value plays a critical role in making decisions about hypotheses and in estimating the confidence we can have in our conclusions.
Normal distribution: Normal distribution is a continuous probability distribution that is symmetric around its mean, showing that data near the mean are more frequent in occurrence than data far from the mean. This bell-shaped curve is crucial in statistics because it describes how many real-valued random variables are distributed, allowing for various interpretations and applications in different areas.
Central Limit Theorem: The Central Limit Theorem (CLT) states that, regardless of the original distribution of a population, the sampling distribution of the sample mean will approach a normal distribution as the sample size increases. This is a fundamental concept in statistics because it allows for making inferences about population parameters based on sample statistics, especially when dealing with larger samples.
Independence: Independence in probability refers to the situation where the occurrence of one event does not affect the probability of another event occurring. This concept is vital for understanding how events interact in probability models, especially when analyzing relationships between random variables and in making inferences from data.
Law of Large Numbers: The Law of Large Numbers states that as the number of trials or observations increases, the sample mean will converge to the expected value or population mean. This principle highlights how larger samples provide more reliable estimates, making it a foundational concept in probability and statistics.
Type II Error: A Type II error occurs when a statistical test fails to reject a null hypothesis that is actually false. This means that the test concludes there is no effect or difference when, in reality, an effect or difference does exist. Understanding Type II error is crucial as it relates to the power of a test, which is the probability of correctly rejecting a false null hypothesis, and its implications can be significant in fields such as medicine and social sciences.
Hypothesis testing: Hypothesis testing is a statistical method used to make inferences or draw conclusions about a population based on sample data. It involves formulating a null hypothesis and an alternative hypothesis, then using sample data to determine whether to reject the null hypothesis. This concept is fundamental when applying various statistical distributions, making predictions based on sample means, and establishing confidence in results derived from data analysis.
Sampling distribution: A sampling distribution is the probability distribution of a statistic obtained through repeated sampling from a population. It describes how the values of a statistic, like the sample mean, vary from sample to sample, and helps in understanding the behavior of estimates as sample sizes change. This concept connects deeply with ideas about normal distributions, central limit theorem, and statistical inference, illustrating how sample statistics can be used to make inferences about the population parameters.
Type I Error: A Type I error occurs when a null hypothesis is incorrectly rejected, indicating that a supposed effect or difference exists when, in reality, it does not. This error is significant in statistical testing as it can lead to false conclusions about the data being analyzed, impacting decisions based on those findings. The implications of a Type I error can be particularly critical in various real-world applications, influencing areas such as medicine, quality control, and social sciences.
Population mean: The population mean is the average value of a given set of data points within a specific population. This term is crucial for understanding how data can be summarized and analyzed, especially when considering how sample means relate to the population mean as described in various statistical concepts. The population mean is also integral to the central limit theorem, which helps explain how sampling distributions behave as sample sizes increase.
Standard Error: Standard error is a statistical term that measures the accuracy with which a sample represents a population. It is the standard deviation of the sampling distribution of a statistic, commonly the mean, and provides insight into how much variability one can expect from sample means if you were to repeatedly draw samples from the same population. Understanding standard error is crucial for interpreting results in the context of the central limit theorem and its applications.
Sample mean: The sample mean is the average value calculated from a set of observations or data points taken from a larger population. This statistic serves as an estimate of the population mean and is crucial in understanding the behavior of sample data in relation to theoretical principles such as convergence and distribution. It plays a significant role in assessing the reliability of estimates, understanding variability, and applying key statistical theorems to analyze real-world data.
Uniform Distribution: Uniform distribution is a type of probability distribution in which all outcomes are equally likely to occur within a specified interval. This concept is key for understanding continuous random variables, where any value within the range has the same probability density. It serves as a fundamental example in probability theory, illustrating how randomness can be evenly spread across a range, which has important implications for applications in statistics and real-world scenarios.
Exponential distribution: The exponential distribution is a continuous probability distribution that describes the time between events in a Poisson process, where events occur continuously and independently at a constant average rate. It is particularly useful for modeling the time until an event occurs, such as the lifespan of electronic components or the time until a customer arrives at a service point.
Mean: The mean is a measure of central tendency that represents the average value of a set of numbers. It is calculated by summing all values in a dataset and then dividing by the total number of values. This concept plays a crucial role in understanding various types of distributions, helping to summarize data and make comparisons between different random variables.
Standard Deviation: Standard deviation is a statistic that measures the dispersion or variability of a set of values around their mean. A low standard deviation indicates that the values tend to be close to the mean, while a high standard deviation suggests that the values are spread out over a wider range. This concept is crucial in understanding the behavior of both discrete and continuous random variables, helping to quantify uncertainty and variability in data.