
3.1 Unit 3: Electric Circuits
6 min read•december 31, 2022
Peter Apps
Peter Apps
3.0: Overview
Unit 3 is all about connecting electrical devices together. We'll look at different types of , how to calculate the flow of electricity through a circuit, and do some analysis of the , , and in various locations in a circuit.
This unit makes up 17-23% of the AP exam and will take 13-26 days to cover depending on class length. The Unit 3 personal progress checkpoint on AP Classroom has around 35 multiple choice questions and 1 free response question for you to practice and check your understanding with.
Make sure to read this important note:
3.1: Circuit Quantities
In Unit 1, we studied voltage and defined it as work per unit charge. There are 2 other important quantities used along with voltage to describe the features of a circuit: and resistance.
A common analogy for how voltage, , and are related to each other is to think of an electric circuit like water flowing through a hose. Voltage is similar to the water pressure, is similar to the amount of water that gets through the hose, and is similar to mud or dirt that gets stuck in the hose and starts to clog it.

Image from freeingenergy.com
Current
is defined as the rate at which charge flows through a circuit. It's represented by the equation:
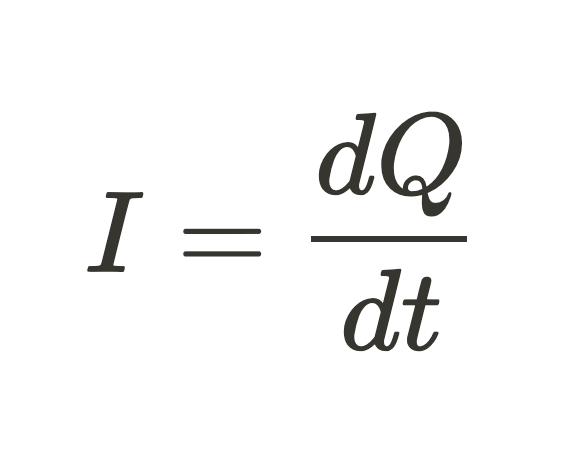
where I is the (measured in Amps or milliAmps), Q is the charge passing a given point, and t is the time for the charge to pass through that point.
On a microscopic level, is also related to the drift velocity (v_d) of the individual charge carriers. Drift velocity can be thought of as the average velocity of each charge carrier as it moves through a wire. In the image below, we're looking at the path of the electron as it moves through a wire.
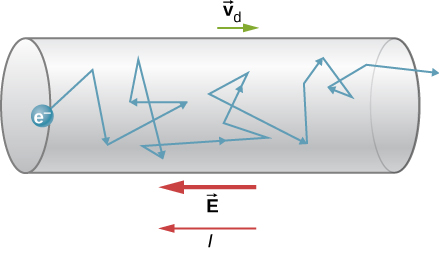
Image from openstax.org
We can imagine that the in the wire would depend on the total number of charge carriers moving through the wire as well. A larger diameter wire would allow for more carriers. Combining these ideas together we can derive an equation for .
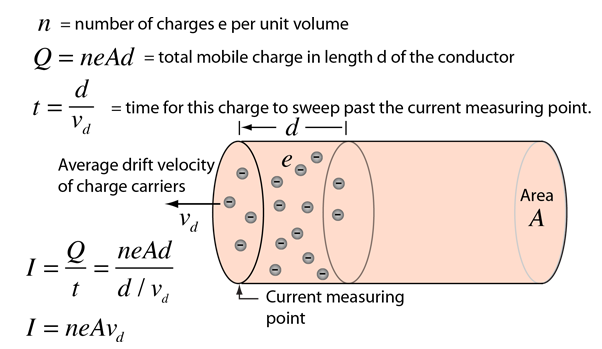
Image from hyperphysics
Density is a third way of describing the in terms of the electric field, E, and the material it is traveling through. In this case, we define density as a vector, J . We then relate the electric field to the density through the equation below. (For a full derivation of this equation, check out this link)

p is the proportionality constant between E and J and is called the . describes how much a given material restricts the . depends on temperature (higher temperatures result in a higher , but most tables give values for 20 C)
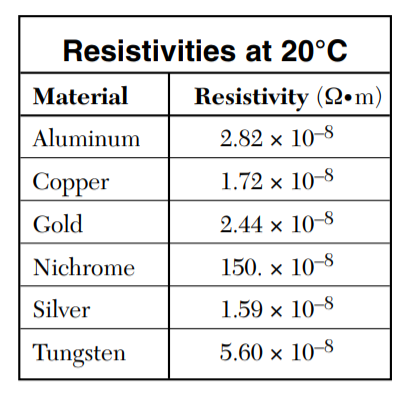
Data from NYS Physics Reference Tables
Resistance
While describes how much a material restricts the , (R) is much more useful for describing a circuit. It takes into account the length (L) and cross-sectional area (A) of the conductor as well.
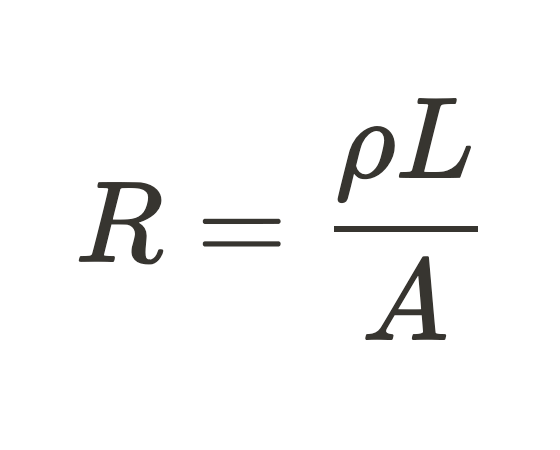
is defined as the opposition to and can be a very useful feature when trying to design a circuit. For example, if the gets too high in a cell phone, the battery starts expanding and can catch fire or explode. However, there are also times where you want to keep the as low as possible (such as transmitting electricity from a plant to people's homes). is measured in Ohms(Ω), where
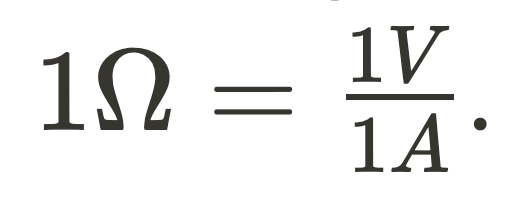
Ohm's Law
The basic mathematical relationship between and is defined by . Depending on your context, it's written one of 3 ways. It doesn't actually matter which one you're more familiar with since they're all the same equation.
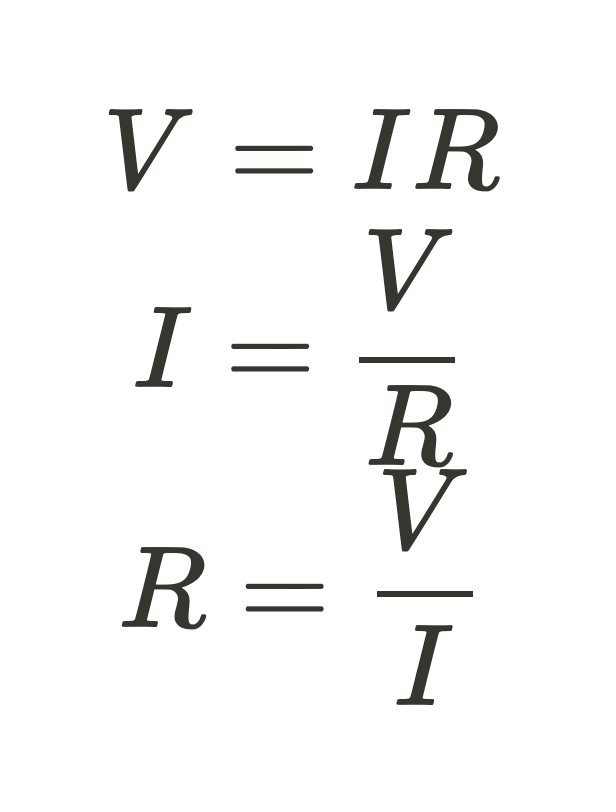
This law relates our three main circuit quantities in a nice simple equation. You will often see this represented in graphical form and be asked to infer if the device is Ohmic or non-Ohmic. As you can see in the graph below, an Ohmic device has a constant linear slope, while a non-Ohmic device does not. Sometimes a device can have an Ohmic region, then become non-ohmic.

Image from www.menihek.ca/
Power
is the rate at which electrical energy is used in a circuit. While the reference tables only show one equation to calculate , you can use Ohm’s law to tweak the equation to use whatever terms you are given (∆V, I, and R). We'll talk about this more in-depth with the next guide, but it's good to understand how it comes from in this section!
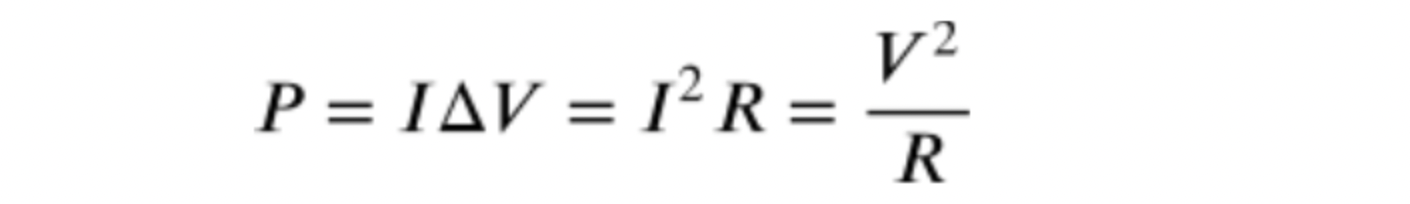
Circuit Symbols & Measuring Tools
To easily draw , we use a variety of symbols to represent common components. Here are a few common ones, and there are many many more that are not used in AP Physics C EM (although if you become an electrical engineer you'll use them!). The ones that you can ignore are the DC supply, junction of conductors, crossing conductors, microphone, loudspeaker, light emitting diode, fuse, alternating signal, thermistor, and light dependent resistor. You will also see the inductor in AP Physics C: Electricity & Magnetism, but you won't use it until you get to unit 5 😉.
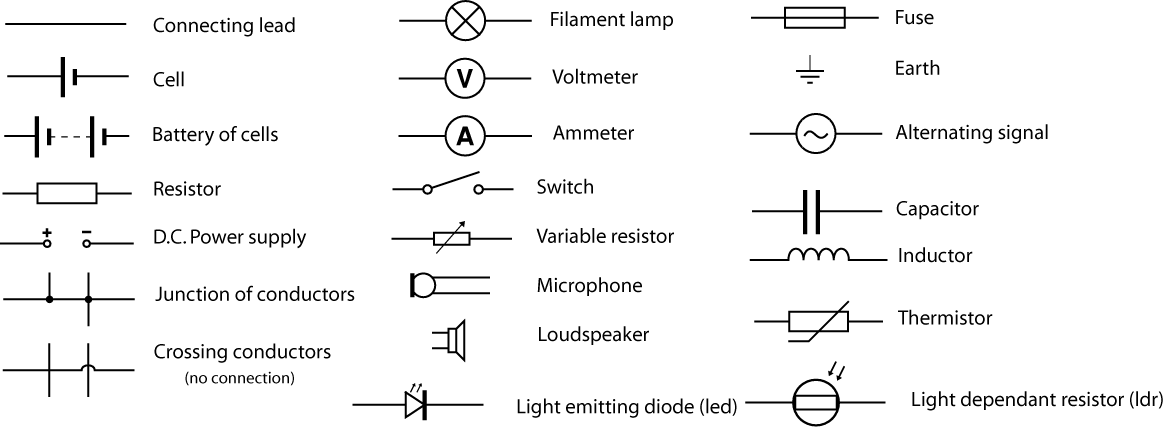
Image from wikimedia.org
The and are two tools that are used to measure different aspects of an electrical circuit. The is used to measure the (remember this from Unit 1!) between two points and is connected in parallel around the component being measured. It has a high internal to avoid creating a short circuit when measuring. The , on the other hand, is used to measure the flowing through a part of the circuit and is connected in series with the component being measured. Its internal is low to accurately measure the . It is important to be careful when using these tools and to ensure they are correctly configured, as incorrect use can lead to short or faulty readings when doing lab work.
Drawing Parallel vs Series Circuits
There are two main ways to connect components in an electrical circuit: series or parallel. In a series connection, the components are arranged in a single line, and the flows through one path. In a , the components are arranged with multiple paths for the to flow through. This means that the is divided between the available paths.
Practice Question
Image from AP Classroom
Answer
Choice B is correct. Because the of a wire depends on

a longer length and smaller area will result in the greatest .
Key Terms to Review (13)
Ammeter
: An ammeter is an instrument used to measure the electric current flowing through a circuit. It tells us how many charges are passing through it per unit time.Circuit Symbols
: Circuit symbols are graphical representations used to represent different electronic components and devices in circuit diagrams. These symbols provide an easy way to understand and communicate complex circuits without having to draw detailed illustrations.Circuits
: Circuits are pathways that allow the flow of electric current. They consist of components such as resistors, capacitors, and inductors connected by conductive wires.Current
: Current refers to the flow of electric charge in an electric circuit. It represents the rate at which charges pass through a given cross-sectional area of a conductor and is measured in amperes (A).Electric power
: Electric power refers to the rate at which electrical energy is transferred or consumed in an electrical system. It measures how quickly work can be done or energy can be transformed within circuits.Ohm's Law
: Ohm's Law states that the current flowing through a conductor between two points is directly proportional to the voltage across the two points, and inversely proportional to the resistance between them.Parallel Circuit
: A parallel circuit is an electric circuit where multiple components are connected side by side with separate paths for current flow. In this type of circuit, each component has the same voltage across its terminals.Potential Difference
: Potential difference, also known as voltage, is the difference in electric potential energy per unit charge between two points in an electric circuit. It represents how much work is done on each unit of charge when it moves from one point to another.Power
: Power is the rate at which work is done or energy is transferred in a circuit. It is measured in watts (W) and can be calculated by multiplying voltage and current.Resistance
: Resistance is a measure of how much a material or device opposes the flow of electric current. It is determined by the material's properties and geometry, and it is measured in ohms.Resistivity
: Resistivity is an intrinsic property of a material that quantifies how strongly it resists the flow of electric current.Series Circuit
: A series circuit is an electric circuit where the components are connected one after another in a single path. In this type of circuit, the same current flows through each component.Voltmeter
: A voltmeter is an instrument used to measure the potential difference or voltage across two points in a circuit. It measures how much electrical energy is being transferred between those points.3.1 Unit 3: Electric Circuits
6 min read•december 31, 2022
Peter Apps
Peter Apps
3.0: Overview
Unit 3 is all about connecting electrical devices together. We'll look at different types of , how to calculate the flow of electricity through a circuit, and do some analysis of the , , and in various locations in a circuit.
This unit makes up 17-23% of the AP exam and will take 13-26 days to cover depending on class length. The Unit 3 personal progress checkpoint on AP Classroom has around 35 multiple choice questions and 1 free response question for you to practice and check your understanding with.
Make sure to read this important note:
3.1: Circuit Quantities
In Unit 1, we studied voltage and defined it as work per unit charge. There are 2 other important quantities used along with voltage to describe the features of a circuit: and resistance.
A common analogy for how voltage, , and are related to each other is to think of an electric circuit like water flowing through a hose. Voltage is similar to the water pressure, is similar to the amount of water that gets through the hose, and is similar to mud or dirt that gets stuck in the hose and starts to clog it.

Image from freeingenergy.com
Current
is defined as the rate at which charge flows through a circuit. It's represented by the equation:
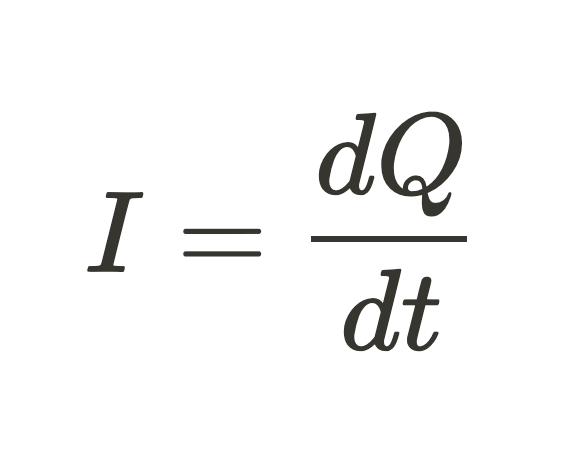
where I is the (measured in Amps or milliAmps), Q is the charge passing a given point, and t is the time for the charge to pass through that point.
On a microscopic level, is also related to the drift velocity (v_d) of the individual charge carriers. Drift velocity can be thought of as the average velocity of each charge carrier as it moves through a wire. In the image below, we're looking at the path of the electron as it moves through a wire.

Image from openstax.org
We can imagine that the in the wire would depend on the total number of charge carriers moving through the wire as well. A larger diameter wire would allow for more carriers. Combining these ideas together we can derive an equation for .

Image from hyperphysics
Density is a third way of describing the in terms of the electric field, E, and the material it is traveling through. In this case, we define density as a vector, J . We then relate the electric field to the density through the equation below. (For a full derivation of this equation, check out this link)

p is the proportionality constant between E and J and is called the . describes how much a given material restricts the . depends on temperature (higher temperatures result in a higher , but most tables give values for 20 C)

Data from NYS Physics Reference Tables
Resistance
While describes how much a material restricts the , (R) is much more useful for describing a circuit. It takes into account the length (L) and cross-sectional area (A) of the conductor as well.
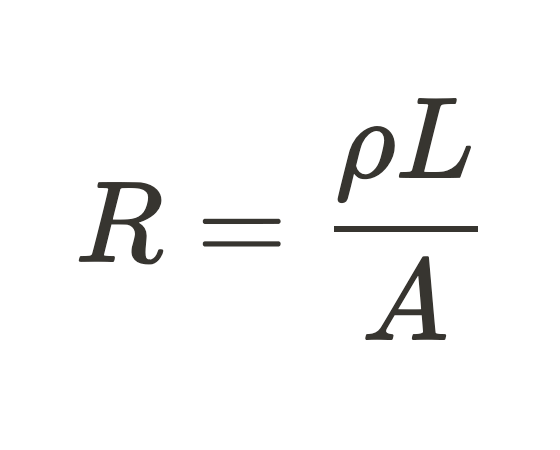
is defined as the opposition to and can be a very useful feature when trying to design a circuit. For example, if the gets too high in a cell phone, the battery starts expanding and can catch fire or explode. However, there are also times where you want to keep the as low as possible (such as transmitting electricity from a plant to people's homes). is measured in Ohms(Ω), where
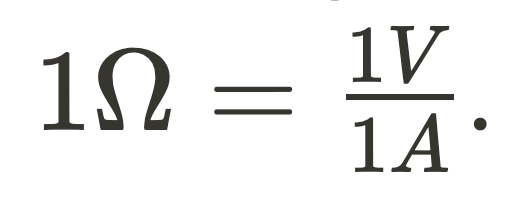
Ohm's Law
The basic mathematical relationship between and is defined by . Depending on your context, it's written one of 3 ways. It doesn't actually matter which one you're more familiar with since they're all the same equation.
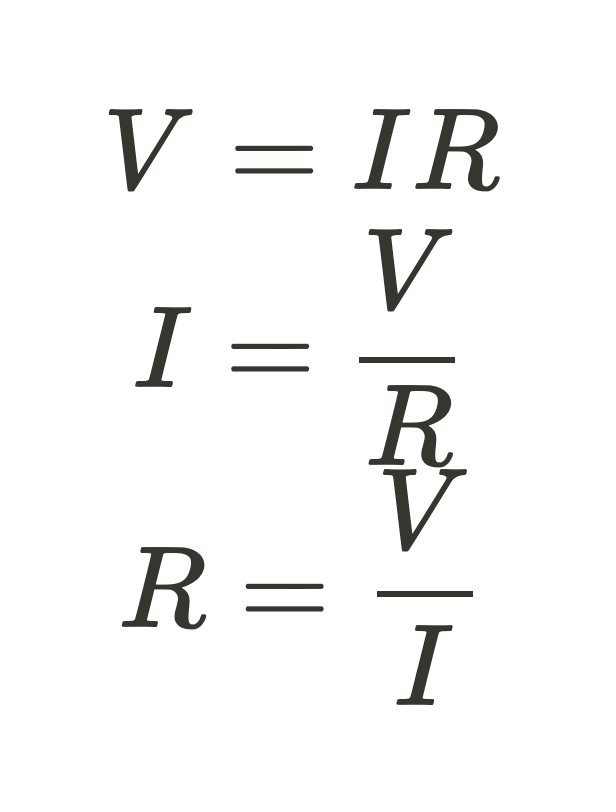
This law relates our three main circuit quantities in a nice simple equation. You will often see this represented in graphical form and be asked to infer if the device is Ohmic or non-Ohmic. As you can see in the graph below, an Ohmic device has a constant linear slope, while a non-Ohmic device does not. Sometimes a device can have an Ohmic region, then become non-ohmic.

Image from www.menihek.ca/
Power
is the rate at which electrical energy is used in a circuit. While the reference tables only show one equation to calculate , you can use Ohm’s law to tweak the equation to use whatever terms you are given (∆V, I, and R). We'll talk about this more in-depth with the next guide, but it's good to understand how it comes from in this section!
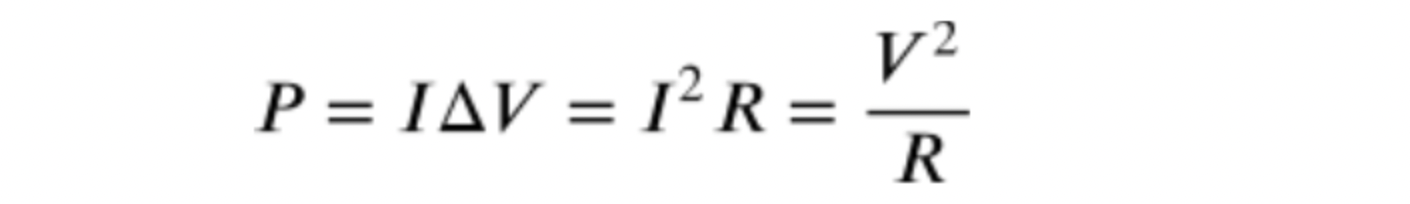
Circuit Symbols & Measuring Tools
To easily draw , we use a variety of symbols to represent common components. Here are a few common ones, and there are many many more that are not used in AP Physics C EM (although if you become an electrical engineer you'll use them!). The ones that you can ignore are the DC supply, junction of conductors, crossing conductors, microphone, loudspeaker, light emitting diode, fuse, alternating signal, thermistor, and light dependent resistor. You will also see the inductor in AP Physics C: Electricity & Magnetism, but you won't use it until you get to unit 5 😉.

Image from wikimedia.org
The and are two tools that are used to measure different aspects of an electrical circuit. The is used to measure the (remember this from Unit 1!) between two points and is connected in parallel around the component being measured. It has a high internal to avoid creating a short circuit when measuring. The , on the other hand, is used to measure the flowing through a part of the circuit and is connected in series with the component being measured. Its internal is low to accurately measure the . It is important to be careful when using these tools and to ensure they are correctly configured, as incorrect use can lead to short or faulty readings when doing lab work.
Drawing Parallel vs Series Circuits
There are two main ways to connect components in an electrical circuit: series or parallel. In a series connection, the components are arranged in a single line, and the flows through one path. In a , the components are arranged with multiple paths for the to flow through. This means that the is divided between the available paths.
Practice Question
Image from AP Classroom
Answer
Choice B is correct. Because the of a wire depends on

a longer length and smaller area will result in the greatest .
Key Terms to Review (13)
Ammeter
: An ammeter is an instrument used to measure the electric current flowing through a circuit. It tells us how many charges are passing through it per unit time.Circuit Symbols
: Circuit symbols are graphical representations used to represent different electronic components and devices in circuit diagrams. These symbols provide an easy way to understand and communicate complex circuits without having to draw detailed illustrations.Circuits
: Circuits are pathways that allow the flow of electric current. They consist of components such as resistors, capacitors, and inductors connected by conductive wires.Current
: Current refers to the flow of electric charge in an electric circuit. It represents the rate at which charges pass through a given cross-sectional area of a conductor and is measured in amperes (A).Electric power
: Electric power refers to the rate at which electrical energy is transferred or consumed in an electrical system. It measures how quickly work can be done or energy can be transformed within circuits.Ohm's Law
: Ohm's Law states that the current flowing through a conductor between two points is directly proportional to the voltage across the two points, and inversely proportional to the resistance between them.Parallel Circuit
: A parallel circuit is an electric circuit where multiple components are connected side by side with separate paths for current flow. In this type of circuit, each component has the same voltage across its terminals.Potential Difference
: Potential difference, also known as voltage, is the difference in electric potential energy per unit charge between two points in an electric circuit. It represents how much work is done on each unit of charge when it moves from one point to another.Power
: Power is the rate at which work is done or energy is transferred in a circuit. It is measured in watts (W) and can be calculated by multiplying voltage and current.Resistance
: Resistance is a measure of how much a material or device opposes the flow of electric current. It is determined by the material's properties and geometry, and it is measured in ohms.Resistivity
: Resistivity is an intrinsic property of a material that quantifies how strongly it resists the flow of electric current.Series Circuit
: A series circuit is an electric circuit where the components are connected one after another in a single path. In this type of circuit, the same current flows through each component.Voltmeter
: A voltmeter is an instrument used to measure the potential difference or voltage across two points in a circuit. It measures how much electrical energy is being transferred between those points.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
