13.2 Error Correction Codes

Error Correction Techniques

Error correction techniques let receivers fix errors that occur during transmission without needing the sender to resend data. This is what separates them from error detection methods, which can only flag that something went wrong. Understanding how these codes work is central to building reliable network systems.

Forward error correction (FEC) is the main strategy here. By adding redundant data to messages before transmission, FEC gives the receiver enough information to both detect and correct errors on its own. This is especially valuable in one-way communications (like satellite broadcasts) and high-noise environments where retransmission is costly or impossible.

Error Detection vs. Error Correction

These two categories solve different problems, and it's worth being precise about the distinction:

• Error detection techniques identify that errors exist in transmitted data but cannot fix them. The receiver's only option is to request retransmission. Common examples:
  • Parity bits
  • Checksums
  • Cyclic redundancy checks (CRC)
• Error correction techniques identify where errors are and fix them, allowing the receiver to recover the original data without retransmission. Common examples:
  • Hamming codes
  • Reed-Solomon codes
  • Other FEC schemes

The tradeoff is straightforward: correction codes require more redundant bits than detection codes, which means higher overhead. But they eliminate the delay and bandwidth cost of retransmission.

Forward Error Correction (FEC)

FEC works by encoding extra information into the transmitted message so the receiver can independently correct errors. Here's how the process flows:

1. The sender applies an error-correcting code to the original data, generating redundant bits or symbols.
2. The redundant information is appended to the original data, forming a codeword.
3. The codeword is transmitted over the channel (where errors may be introduced).
4. The receiver uses the code's decoding algorithm to detect and correct any errors.
5. The original data is extracted from the corrected codeword.

Advantages of FEC:

• Reduces the need for retransmissions, which improves both throughput and latency
• Suitable for one-way communication or broadcasting, where there's no return channel (e.g., satellite TV)
• Effective in high-noise environments or when retransmission is impractical (e.g., deep space communications, where round-trip times can be minutes or hours)

Error Correction Codes

Hamming Codes

Hamming codes are linear error-correcting codes that insert parity bits at specific positions within a codeword. The positions of these parity bits are powers of 2 (positions 1, 2, 4, 8, ...), and each parity bit covers a particular subset of data bits based on their binary position values.

• Each parity bit is calculated so that the group of bits it covers has even (or odd) parity.
• Single-bit error correction: If one bit flips during transmission, the parity checks will produce a nonzero pattern called the syndrome, which directly identifies the position of the error. The receiver flips that bit to correct it.
• Double-bit error detection: Hamming codes can detect (but not correct) two-bit errors. Adding an overall parity bit to the code (called SECDED: Single Error Correction, Double Error Detection) lets you distinguish between single and double errors.

A key concept here is Hamming distance, which is the minimum number of bit positions in which any two valid codewords differ. For standard Hamming codes, the minimum Hamming distance is 3. That's what gives them the ability to correct 1-bit errors and detect 2-bit errors.

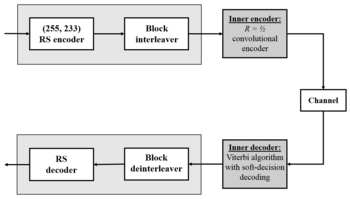
Reed-Solomon Codes

Reed-Solomon codes take a different approach. Instead of working with individual bits, they operate on symbols, where each symbol is a group of bits (commonly 8 bits, making each symbol one byte).

• Redundant symbols are appended to the data symbols to form a codeword.
• A Reed-Solomon code that adds $2t$ redundant symbols can correct up to $t$ symbol errors. This means even if multiple bits within a single symbol are corrupted, it counts as just one symbol error.
• This makes Reed-Solomon codes particularly effective against burst errors, where consecutive bits get corrupted together. A burst that damages several bits in a row may only affect one or two symbols.

Reed-Solomon codes are widely used in:

• Storage devices: CDs, DVDs, and Blu-ray discs use them to handle scratches and surface defects
• Data transmission: Satellite communications, DSL, and digital television broadcasting
• QR codes: The error correction that lets you scan a partially damaged QR code is Reed-Solomon

Applying Error Correction in Practice

The encoding and decoding process follows a consistent pattern regardless of the specific code used:

Encoding (sender side):

1. Select the appropriate error correction code based on the channel's expected error rate and the application's requirements.
2. Generate redundant bits or symbols according to the code's rules.
3. Append the redundant information to the original data to form the codeword.

Decoding (receiver side):

1. Receive the codeword, which may contain errors introduced during transmission.
2. Run the code's decoding algorithm to detect errors and compute their locations.
3. Correct the identified errors.
4. Extract the original data from the corrected codeword.

Where you'll see this in real systems:

• Hard drives and SSDs use error correction to handle media defects and read errors
• Wireless communication protocols (Wi-Fi, cellular) rely on FEC to cope with signal interference and fading
• Industrial control systems use these techniques to ensure reliable data transfer in electrically noisy environments