So far, we’ve defined limits, used limit notation, and estimated limit values from graphs. In this study guide, we’ll cover how to estimate limit values from tables given to you. 🎯
Concept of a Limit Recap
As our previous key topic guides have mentioned, a limit is the value at which x is near the target number a is defined. It is typically written like the example below:
Here, we see that the arrow indicates that x is approaching the target number a and L represents the limit of the function when x is close or near the target number a. There are several ways of finding a limit for a function, and one of these ways will be discussed in the following section. 🔢

One-Sided Limits
Before we begin, it is also important to understand the concept of one-sided limits, where the limit is defined as x approaching the target number, a, from either the left or right side of the number line. You could think of this as the left side going from numbers less than the target number and the right side going from numbers greater than the target number.
Whether or not a limit is coming from the left or right side of the target value is indicated using a plus sign (+), meaning it approaches from the right ⬅️, or a minus sign (-), meaning it approaches from the left ➡️, at the top corner of the target value
Using a Table to Estimate Limits
In some cases, direct substitution of the target number does not work in solving for a limit of a function because it leads to an indeterminable type (which is a topic discussed later in the course). ❌ Essentially, you cannot substitute the target value directly into the function because the output will be undefined, as the example below displays:
Here we see that if we try to use the direct substitution method by plugging in 0 into the function, we get $\frac{0}{0}$, which is undefined and implies that the limit of the function at 0 is also undefined.
So to solve for the limit of these particular functions, x-values close to the target number a from both the left and right sides of the number line can be substituted into the function. In doing so, the outputs from both sides of the target number will approach a certain output value, which would be considered the limit of the function at the target number a. ↔️
To make it more organized, we use a table to list the values less than or greater than the target number in the top row and list the limit of the function at those values on the next row. An example is displayed below for better understanding. 📚

The table shows a list of x-values greater than and less than 0 and the y-values of these numbers from f(x), as the y-values approach the same number from the left and right sides.
Image courtesy of Calculus: 9th Edition by Larson and Edward.
This table results from substituting x-values near 0 from the left and right sides in the function mentioned above and calculating their outputs 📱. As displayed in the table…
- As the x-values get closer to 0 from the right side, the y-values are getting closer to 2.
- As the x-values from the left side get closer to 0, the y-values are also getting closer to 2, but the y-values of this function never actually reach 2.
Based on the movement of the y-values as the x-values approach 0, we can estimate that the limit of the function at x = 0 would be 2.
💡 When we refer to x-values near or close to the target value a, these are numbers in close proximity to a from the left and right sides of the target value. For example, if the target value is a = 1, then numbers considered near or close to 1 would include 0.9, 0.99, and 0.999 from the left side, as well as 1.001, 1.01, and 1.1 from the right side.
Keep in mind that for this method to work, the limit from the left AND right side relative to the target number has to be approaching the SAME output value, as the example above shows.
In cases where this method does not work, such as the limit of the function from the left and right sides of the target number a are not approaching the same y-value, it could imply that a vertical asymptote exists in this function at the target number, which will be explained in future key topic guides throughout the unit. 📈
Practice Evaluating Limits from a Table
Question courtesy of Calculus 9th Edition by Larson and Edward textbook.
To begin solving for the limit, a table of x-values that are greater and less than 4 needs to be made.
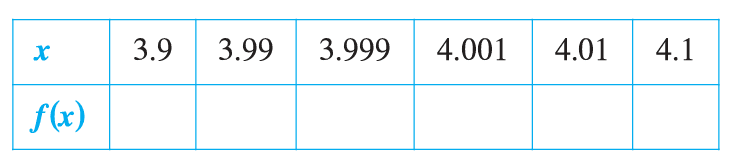
The table above contains x-values greater than and less than 4 which are to be inputted into f(x) to find their corresponding y-values and determine the limit of the function a x approaches 4.
Image courtesy of Calculus 9th Edition by Larson and Edward.
Now that we have the table made, we can plug each x-value into the function to find the y-value that is being approached from the left and right sides.

The table above contains both the x and y values mentioned in the previous table, filled with the y-values that result from inputting the x-values into f(x) to determine the limit of the function.
Image courtesy of Calculus 9th Edition by Larson and Edward
By calculating the y-value for each x-value near 4 from the left and right sides, we can estimate that 0.2 is the limit of the function as x approaches 4 because both the x-values from both left and right sides of the target number 4 are approaching the same y-value, which is 0.2. 💾
💡 The key to solving problems like this is being able to identify x-values near or close to the target number and seeing where the y-values of these numbers approach.
Conclusion
Using a table is one of many ways to solve for limits that cannot be solved through direct substitution. While tedious, it can provide insight into the direction of the y-values when approaching a given x-value, which is critical in solving for limits. Thanks for reading and good luck! ✅
Vocabulary
The following words are mentioned explicitly in the College Board Course and Exam Description for this topic.
| Term | Definition |
|---|---|
| function | A mathematical relationship that assigns exactly one output value to each input value of an independent variable. |
| limit | The value that a function approaches as the input approaches some value, which may or may not equal the function's value at that point. |
Frequently Asked Questions
How do I find limits when I only have a table of values?
Use the table to see what f(x) does as x approaches the target from the left and the right. Steps you can use: 1. Pick x-values in the table that get close to the point from the left and from the right. Compute the corresponding f(x) values (or use the given ones). 2. Estimate the left-hand limit by seeing where f(x) is heading as x→a− and the right-hand limit as x→a+. If they’re about equal, that’s the two-sided limit. If they differ, the two-sided limit does not exist (jump discontinuity). 3. If values blow up (grow without bound) toward ±∞, that suggests an infinite limit/vertical asymptote. 4. If table gives values that approach the same finite number but f(a) is different or undefined, you’ve found a removable discontinuity (limit exists). 5. For more accuracy, do a simple linear interpolation between the two closest points on each side or use more table points to see the trend. Remember AP language: check one-sided limits, two-sided limit, and note indeterminate 0/0 situations (you’d need algebra there). Numerical estimation is an accepted AP approach (EK LIM-1.C.5). For practice and more examples, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and more practice problems (https://library.fiveable.me/practice/ap-calculus).
What's the formula for estimating limits from tables?
There isn’t a single fancy formula—you estimate a limit from a table by looking at f(x) values as x gets closer to the point a. In symbols: - Right-hand estimate: lim_{x→a^+} f(x) ≈ f(a + h) for very small positive h (use several decreasing h). - Left-hand estimate: lim_{x→a^-} f(x) ≈ f(a − h) for very small positive h. - Two-sided: lim_{x→a} f(x) ≈ values of f(a ± h); the limit exists if left and right estimates agree. Practical steps: pick sequences of x-values approaching a from left and right, record f(x), and see whether values appear to converge. If they do, use the nearest values (or average the closest left and right) as your estimate. If values blow up, suspect an infinite/vertical asymptote or discontinuity. For 0/0 indeterminate forms, use the table plus algebraic simplification (if possible) to get closer values. For AP guidance and examples, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and try many practice problems (https://library.fiveable.me/practice/ap-calculus).
When do I use tables vs graphs to find limits?
Use a table when you want a numerical estimate of a limit; use a graph when you need a visual idea of behavior. Concretely: - Tables: plug x-values that approach the point from the left and right (e.g., 2.9, 2.99 and 3.1, 3.01) to estimate one-sided limits and a two-sided limit by seeing whether the left- and right-hand values converge to the same number. Tables are ideal for indeterminate forms like 0/0, removable holes, or when you need a decimal approximation (CED EK LIM-1.C.5 keywords: table of values, numerical estimation, one-sided limit). - Graphs: use when the function’s shape matters—detect jump discontinuities, vertical asymptotes (values blowing up), or oscillation near the point. Graphs make it easy to spot whether the left and right limits differ (jump) or go to ±∞ (infinite limit). On the AP exam: Part A (no calculator) often gives graphs; Part B (calculator allowed) may give tables or let you generate values. For practice on estimating limits from tables, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and try practice problems (https://library.fiveable.me/practice/ap-calculus).
Can someone explain step by step how to read limit values from a data table?
Start by picking the x-value a limit is asking about (call it a). Then read the table values for x approaching a from the left and from the right: 1. Make two lists: x-values < a (left) with their f(x), and x-values > a (right) with their f(x). These give left-hand and right-hand behavior (one-sided limits). 2. Look at values closer to a—e.g., x = a ± 0.1, ±0.01 if present. Ask: do the left f(x) values seem to approach the same number L as the right f(x) values? If both sides approach L, the two-sided limit = L. 3. If left and right approach different numbers, the two-sided limit does not exist (jump discontinuity). If values blow up in magnitude (grow ± large) as x→a, suspect an infinite limit / vertical asymptote. 4. If table shows 0/0-like behavior or missing f(a) but both sides approach the same L, it’s a removable discontinuity—the limit exists even if f(a) isn’t defined. 5. If table spacing is coarse, use linear interpolation between nearest points to estimate the trend (tabular convergence). Report the estimated limit and note it’s an approximation. This procedure matches EK LIM-1.C.5 (numerical estimation) in the CED. For more examples and practice, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and Unit 1 overview (https://library.fiveable.me/ap-calculus/unit-1). For lots of practice problems, try (https://library.fiveable.me/practice/ap-calculus).
I don't understand how to tell if a limit exists just from looking at numbers in a table
To decide if a limit exists from a table, compare the left-hand and right-hand values as x gets close to the target point: 1. Identify entries with x-values just less than and just greater than the point a. Those give estimates of the left-hand limit (lim x→a− f(x)) and right-hand limit (lim x→a+ f(x)). 2. If both one-sided estimates approach the same number (to within any reasonable rounding), the two-sided limit exists and equals that common value. 3. If they approach different numbers, the two-sided limit does not exist (jump/discontinuity). 4. If one or both blow up (grow without bound), you’re seeing an infinite limit/vertical asymptote—say the limit doesn’t exist as a finite number. 5. If values approach a number but f(a) is different or undefined, that’s a removable discontinuity (limit still exists). Quick checklist: look at trends from left and right, compare numbers, watch for 0/0-type behavior or huge values. This is exactly what AP asks in Topic 1.4 (LIM-1.C)—practice with tables on the AP study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and try more problems at (https://library.fiveable.me/practice/ap-calculus).
How do I know which x-values to look at when estimating limits from tables?
Look at the x-values that approach the target point from both sides—values just less than the point for the left-hand limit and just greater than the point for the right-hand limit. Use the table entries nearest the point (e.g., if you want lim x→2, focus on x = 1.9, 1.99, 2.1, 2.01 if those are given). Compare the left and right lists: if both sets of y-values approach the same number, that’s the two-sided limit; if they differ, the limit doesn’t exist (or is a jump). If entries give 0/0 or weird behavior, pick values even closer or use linear interpolation between the closest two points to get a better estimate. This is exactly the numerical/tabular approach AP asks for in LIM-1.C (one-sided vs two-sided reasoning). For more practice and examples, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and the Unit 1 overview (https://library.fiveable.me/ap-calculus/unit-1). For extra drills, try problems at (https://library.fiveable.me/practice/ap-calculus).
What's the difference between left-hand and right-hand limits in a table?
Left-hand limit (limit as x → a−) uses the table entries with x-values less than a—you look at f(x) for numbers approaching a from the left and see what value those outputs seem to approach. Right-hand limit (limit as x → a+) uses entries with x > a and looks at values approaching from the right. How to use a table: pick rows with x-values getting closer to a from each side, list the f(x) values, and see their trend. If the left-hand and right-hand one-sided estimates approach the same number, the two-sided limit exists and equals that number. If they approach different numbers, you have a jump (two-sided limit does not exist); if one or both blow up, you may have an infinite/vertical asymptote; if table values approach a finite value but f(a) is different or undefined, that’s a removable discontinuity. This is exactly what Topic 1.4 (LIM-1.C) practices—see the study guide for examples (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT). For more practice problems, try https://library.fiveable.me/practice/ap-calculus.
Why do my limit estimates keep being wrong when I use the table method?
Most likely you’re missing one of these common issues when using tables to estimate limits. - Not checking both one-sided limits: a two-sided limit exists only if left- and right-hand estimates agree. If they don’t, the limit is nonexistent (jump/discontinuity). - Picking x-values too far or unevenly spaced: use values that get closer to the target from each side (e.g., 0.1, 0.01) so the table shows tabular convergence. - Hitting an indeterminate form (0/0) or near-vertical asymptote: values can blow up or oscillate, so algebraic simplification or a graph is needed. - Rounding/precision errors: small differences can be lost if you round too early. Keep extra decimals. - Oscillation: functions like sin(1/x) don’t settle—tables won’t give a meaningful number. Fixes: compute values from both sides with smaller step sizes, check for 0/0 and simplify algebraically, sketch or use a graphing calculator to confirm behavior. For AP-specific practice and examples on estimating limits from tables, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and lots of practice problems (https://library.fiveable.me/practice/ap-calculus).
How do I estimate limits when the x-value I need isn't actually in the table?
If the x-value you need isn’t in the table, estimate the limit by looking at values that approach that x from both sides and seeing where the function seems to converge. Steps (quick): - Use the nearest x-values left and right of the target. Compute f(x) for those and for any closer points if given (these are one-sided estimates). - If left- and right-hand estimates approach the same number, that’s your two-sided limit. If they differ, the two-sided limit does not exist. - If the table gives values that get steadily closer (tabular convergence), read off the value they approach. - If entries give 0/0 behavior or blow up, suspect a removable discontinuity (use algebra to simplify) or a vertical asymptote (values grow large with sign → infinite limit or DNE). - For a better numeric estimate you can linearly interpolate between the two closest points. This is exactly the CED idea of using numerical/tabular estimation and one-sided limits (LIM-1.C). For practice, check the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and try problems at (https://library.fiveable.me/practice/ap-calculus).
When the function values in a table are getting really close to some number, is that the limit?
Short answer: usually yes—if the values in a table (from the left and from the right) get arbitrarily close to the same number as x approaches a point, that number is the limit. A few things to check when you’re estimating from a table (CED keywords): - Look at one-sided behavior: check values for x < a (left-hand limit) and x > a (right-hand limit). The two-sided limit exists only if both agree. - Watch for 0/0 indeterminate patterns: tabular values may approach a finite number even if f(a) is undefined (removable discontinuity). - If values blow up (grow very large in magnitude) on either side, that suggests an infinite limit / vertical asymptote, not a finite limit. - Use closer x-values to see if the sequence really settles (tabular convergence); you can linearly interpolate between nearby entries if needed. This is exactly what Topic 1.4 practices. For a quick study guide and more examples, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT). For extra practice problems, check (https://library.fiveable.me/practice/ap-calculus).
I'm confused about how accurate my limit estimate needs to be from a table
You don’t need insane precision from a table—just enough evidence to show the limit’s behavior. Look for a clear trend as x approaches the point: do left- and right-hand values approach the same number (two-sided limit), approach different numbers (limit DNE), or blow up (±∞/vertical asymptote)? Practical tips: - Check both one-sided limits using values closer and closer to the point. If both sides cluster (e.g., 2.98, 2.999, 3.001, 3.02), report the cluster (≈3.00; two decimal places or 2–3 significant digits is fine on the AP). - If values oscillate or jump (e.g., left → 1, right → 4), conclude the limit does not exist (removable vs. jump discontinuity). - If magnitudes grow without bound (100, 1000, 10000), say the limit is ∞ or −∞ (vertical asymptote). - For 0/0-looking entries, note the indeterminate form and use algebra or closer table values to decide. Linear interpolation between very close entries can refine an estimate. On the AP, numerical estimates only need to justify the trend (show values you used). For extra practice and examples see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT), the Unit 1 overview (https://library.fiveable.me/ap-calculus/unit-1), and tons of practice problems (https://library.fiveable.me/practice/ap-calculus).
What do I do if the y-values in the table seem to be approaching two different numbers?
If the y-values in a table seem to be approaching two different numbers, you’re seeing left- and right-hand behavior—check one-sided limits. Use values for x just less than the point to estimate the left-hand limit (lim x→a− f(x)) and values just greater to estimate the right-hand limit (lim x→a+ f(x)). - If both one-sided limits approach the same number, the two-sided limit exists and equals that number (removable or regular limit). - If they approach different numbers, the two-sided limit does not exist—that’s a jump discontinuity (or at least a nonexistence of the limit). - If values blow up toward ±∞ on one or both sides, you may have a vertical asymptote (infinite limit). When you’re estimating from tables (CED EK LIM-1.C.5), use closer x-values, possibly linear interpolation between entries, and report one-sided estimates with units if context applies. For more practice and tips on tabular estimation and one-sided limits, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and the Unit 1 overview (https://library.fiveable.me/ap-calculus/unit-1).
How do I write up my work when estimating limits from tables on FRQs?
When you estimate a limit from a table on an FRQ, write your work so a reader can follow your reasoning step-by-step. 1. State the limit you’re estimating and give the relevant table entries (include x values approaching from left and right). 2. Compute numerical estimates: pick values closer to the point from the left and right and show each quotient/plugged value (e.g., f(1.1)=…, f(0.9)=…, then state left-hand ≈ …, right-hand ≈ …). Use consistent decimals/units. 3. Identify one-sided limits explicitly: “lim x→a− f(x) ≈ L1” and “lim x→a+ f(x) ≈ L2.” If L1 and L2 agree (within reason), conclude the two-sided limit equals that number; if not, state the two-sided limit does not exist. 4. If the table suggests 0/0 or removable behavior, note that and mention linear interpolation or algebraic factorization as justification if appropriate. If values blow up, mention “infinite limit/vertical asymptote.” 5. Give a short interpretation in context (with units) if the problem is applied—AP FRQs often require units and meaning. Show calculations and clear conclusions—AP scorers expect the numeric work, one-sided checks, and a final stated answer (see the Topic 1.4 study guide for examples) (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT). For broader review or extra practice, check the unit page (https://library.fiveable.me/ap-calculus/unit-1) and the practice set (https://library.fiveable.me/practice/ap-calculus).
Can I use my calculator to help estimate limits from table data?
Yes—your calculator can be a helpful tool when estimating limits from a table, but use it wisely. How it helps - Quickly compute one-sided approaches: evaluate f(x) for x values getting closer from left and right and compare (left-hand vs right-hand limits). - Do averages or finite differences to estimate slopes or rates (useful for R′(5)-type work in the CED). - Fit a simple linear interpolation between nearby table entries or compute more precise decimal values (good when values look like they’re approaching a number). - Detect trouble: big jumps in values suggest a jump discontinuity; values blowing up in magnitude suggest an infinite limit/vertical asymptote; 0/0 patterns may need algebraic manipulation, not just a table. Exam rules & tips - Graphing calculators are allowed on Part B (and some free-response items) but not on all parts—know when you can use one. Use the calculator to speed arithmetic and to check whether left and right estimates agree (for a two-sided limit). - Always state the numerical evidence: list the nearby x-values you used and show the trend (that’s expected on AP). For practice, check the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and try extra problems (https://library.fiveable.me/practice/ap-calculus).
What does it mean when a table shows the function values going to infinity?
If a table of values shows f(x) getting larger and larger in magnitude as x approaches a point (e.g., 100, 1,000, 10,000), that’s a sign of an infinite limit. It means the function doesn’t approach a finite number near that x-value—instead f(x) → +∞ or f(x) → −∞. In AP language this often indicates a vertical asymptote or an infinite one-sided limit. How to read the table: - Check left- and right-hand values separately. If both sides blow up to the same infinity (both +∞ or both −∞), we describe a two-sided infinite limit/vertical asymptote. - If one side goes to +∞ and the other to −∞ (or one side stays finite), the two-sided limit does not exist but you can state the one-sided behavior. - Remember: “∞” is not a real limit value—it’s a description of unbounded growth. For more on estimating limits from tables and AP-style practice, see the Topic 1.4 study guide (https://library.fiveable.me/ap-calculus/unit-1/estimating-limit-values-tables/study-guide/OJmciOeNSSLqtWYs9iZT) and the Unit 1 overview (https://library.fiveable.me/ap-calculus/unit-1). For more practice questions, try (https://library.fiveable.me/practice/ap-calculus).