Multistep methods use info from past steps to solve differential equations. They're split into explicit (Adams-Bashforth) and implicit (Adams-Moulton) types. These methods can be more efficient than single-step methods for certain problems.
Stability analysis helps us understand how numerical methods behave. It's crucial for picking the right method and step size, especially for stiff equations. A-stability is a key property that ensures a method remains stable for any step size.
Multistep Methods
Overview of Multistep Methods
- Multistep methods utilize information from previous steps to approximate the solution at the current step
- Involve a linear combination of the function values and derivatives at past time steps
- Require starting values obtained by other methods (Runge-Kutta) to begin the integration process
- Classified into explicit methods (Adams-Bashforth) and implicit methods (Adams-Moulton)
Adams-Bashforth and Adams-Moulton Methods
- Adams-Bashforth methods are explicit multistep methods that use only past values of the function to estimate the current value
- Example: The second-order Adams-Bashforth method uses the formula $y_{n+1} = y_n + \frac{h}{2}(3f(t_n, y_n) - f(t_{n-1}, y_{n-1}))$
- Adams-Moulton methods are implicit multistep methods that use both past and current values of the function
- Example: The second-order Adams-Moulton method uses the formula $y_{n+1} = y_n + \frac{h}{2}(f(t_{n+1}, y_{n+1}) + f(t_n, y_n))$
- Predictor-corrector methods combine an explicit method (predictor) with an implicit method (corrector) to improve accuracy and stability
- The predictor provides an initial estimate for the corrector step, which is then iteratively refined
Backward Differentiation Formulas (BDF)
- BDF methods are implicit multistep methods that use past values of the solution and its derivatives to approximate the current value
- Particularly useful for stiff equations due to their stability properties
- The order of a BDF method refers to the number of past values used in the approximation
- Example: The second-order BDF method uses the formula $y_{n+1} = \frac{4}{3}y_n - \frac{1}{3}y_{n-1} + \frac{2}{3}hf(t_{n+1}, y_{n+1})$
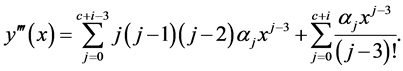
Stability Analysis
Importance of Stability Analysis
- Stability analysis is crucial for understanding the behavior of numerical methods when applied to differential equations
- Determines whether the numerical solution remains bounded and close to the exact solution as the step size decreases
- Helps in selecting appropriate methods and step sizes for a given problem
A-stability and Stiff Equations
- A-stability is a desirable property for numerical methods, especially when dealing with stiff equations
- A method is A-stable if its stability region includes the entire left half-plane of the complex plane
- Ensures that the method remains stable for any step size when applied to equations with negative real eigenvalues
- Stiff equations are characterized by having both fast and slow components in their solutions
- Require methods with good stability properties (A-stability) to avoid excessively small step sizes and maintain efficiency
- Examples of stiff equations include chemical kinetics, electrical circuits, and heat transfer problems
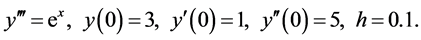
Convergence Properties
Consistency and Convergence
- Consistency refers to the ability of a numerical method to approximate the original differential equation as the step size approaches zero
- A method is consistent if the local truncation error (difference between the numerical and exact solutions over one step) tends to zero as the step size decreases
- Convergence refers to the property of the global error (difference between the numerical and exact solutions over the entire interval) approaching zero as the step size tends to zero
- Convergence is a combination of consistency and stability
- For a method to be convergent, it must be both consistent and stable
Order of Convergence
- The order of convergence quantifies the rate at which the global error decreases as the step size is reduced
- Defined as the exponent $p$ in the relation $\text{global error} \leq Ch^p$, where $C$ is a constant and $h$ is the step size
- A method with order $p$ will have its global error decrease by a factor of $2^p$ when the step size is halved
- Higher-order methods generally provide more accurate solutions for a given step size but may be more computationally expensive
- Example: The fourth-order Runge-Kutta method has a global error proportional to $h^4$, while the Euler method has a global error proportional to $h$