11.8 Solving Systems with Cramer's Rule

Determinants and Cramer's Rule

Calculation of Matrix Determinants

A determinant is a single number (a scalar) computed from the elements of a square matrix. You need determinants to use Cramer's Rule, so this is the place to start.

2×2 Determinant:

$\begin{vmatrix}a & b \\ c & d\end{vmatrix} = ad - bc$

Multiply the main diagonal, then subtract the product of the other diagonal. For example:

$\begin{vmatrix}3 & 2 \\ 1 & 5\end{vmatrix} = (3)(5) - (2)(1) = 15 - 2 = 13$

3×3 Determinant (Cofactor Expansion along the first row):

$\begin{vmatrix}a & b & c \\ d & e & f \\ g & h & i\end{vmatrix} = a(ei - fh) - b(di - fg) + c(dh - eg)$

Notice the pattern: you move across the first row, alternating signs ($+, -, +$). Each element gets multiplied by the determinant of the 2×2 matrix that remains after crossing out that element's row and column.

Here's how to work through a 3×3 determinant step by step:

1. Start with the first-row element $a$. Cross out row 1 and column 1. Compute the 2×2 determinant of what's left: $(ei - fh)$. Multiply by $+a$.

2. Move to the first-row element $b$. Cross out row 1 and column 2. Compute the 2×2 determinant: $(di - fg)$. Multiply by $-b$.

3. Move to the first-row element $c$. Cross out row 1 and column 3. Compute the 2×2 determinant: $(dh - eg)$. Multiply by $+c$.

4. Add all three results together.

Application of Cramer's Rule

Cramer's Rule solves a system of linear equations by replacing columns of the coefficient matrix with the constants and computing determinants. It works for any system where the determinant of the coefficient matrix is not zero.

For a 2×2 system:

$a_1x + b_1y = c_1$ $a_2x + b_2y = c_2$

The solutions are:

$x = \frac{D_x}{D} \quad \text{and} \quad y = \frac{D_y}{D}$

where:

• $D$ is the determinant of the coefficient matrix: $\begin{vmatrix}a_1 & b_1 \\ a_2 & b_2\end{vmatrix}$
• $D_x$ replaces the $x$-column (first column) with the constants: $\begin{vmatrix}c_1 & b_1 \\ c_2 & b_2\end{vmatrix}$
• $D_y$ replaces the $y$-column (second column) with the constants: $\begin{vmatrix}a_1 & c_1 \\ a_2 & c_2\end{vmatrix}$

Example: Solve $2x + 3y = 8$ and $x - y = 1$.

1. Find $D$: $\begin{vmatrix}2 & 3 \\ 1 & -1\end{vmatrix} = (2)(-1) - (3)(1) = -2 - 3 = -5$

2. Find $D_x$: $\begin{vmatrix}8 & 3 \\ 1 & -1\end{vmatrix} = (8)(-1) - (3)(1) = -8 - 3 = -11$

3. Find $D_y$: $\begin{vmatrix}2 & 8 \\ 1 & 1\end{vmatrix} = (2)(1) - (8)(1) = 2 - 8 = -6$

4. Solve: $x = \frac{-11}{-5} = \frac{11}{5}$ and $y = \frac{-6}{-5} = \frac{6}{5}$

The key idea to remember: to find a particular variable, replace that variable's column in the coefficient matrix with the constants column, then divide by $D$.

Extension to Three-Variable Systems

Cramer's Rule extends naturally to 3×3 systems. For:

$a_1x + b_1y + c_1z = d_1$ $a_2x + b_2y + c_2z = d_2$ $a_3x + b_3y + c_3z = d_3$

The solutions follow the same pattern:

$x = \frac{D_x}{D}, \quad y = \frac{D_y}{D}, \quad z = \frac{D_z}{D}$

• $D$ is the determinant of the 3×3 coefficient matrix: $\begin{vmatrix}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{vmatrix}$
• $D_x$: replace the first column ($x$-coefficients) with the constants $d_1, d_2, d_3$
• $D_y$: replace the second column ($y$-coefficients) with the constants
• $D_z$: replace the third column ($z$-coefficients) with the constants

The logic is identical to the 2×2 case. The only difference is that each determinant calculation is now a 3×3 determinant, so there's more arithmetic involved.

Properties of Determinants

These properties can save you time on calculations and help you spot special cases:

• Row/column swap: Interchanging any two rows (or any two columns) flips the sign of the determinant.
• Identical rows/columns: If two rows or two columns are identical, the determinant equals zero.
• Scalar multiplication: Multiplying every entry in a single row (or column) by a scalar $k$ multiplies the entire determinant by $k$. (This is not the same as multiplying the whole matrix by $k$.)
• Row combination: Adding a multiple of one row to another row does not change the determinant. This is useful if you want to create zeros to simplify a 3×3 calculation before expanding.

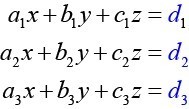
Cramer's Rule vs. Other Methods

Cramer's Rule isn't the only way to solve systems. Here's how it compares:

• Cramer's Rule: Clean and formulaic for 2×2 and 3×3 systems. Every variable gets its own determinant ratio, so you can solve for just one variable if that's all you need. However, the number of determinant calculations grows quickly for larger systems, making it impractical beyond 3×3 in most cases.
• Gaussian Elimination: Converts the augmented matrix to row echelon form using row operations. More efficient for larger systems and the go-to method when systems get big.
• Matrix Inversion: Uses $A^{-1}$ to solve $AX = B$ as $X = A^{-1}B$. Particularly useful when you need to solve several systems that share the same coefficient matrix but have different constant vectors.

For a College Algebra course, you'll mostly use Cramer's Rule on 2×2 and 3×3 systems where it works well.

Systems of Equations and Solutions

Before applying Cramer's Rule, it helps to know what kind of solution a system can have:

• Unique solution: Exactly one set of values satisfies all equations. This is the case when $D \neq 0$, and Cramer's Rule gives you the answer directly.
• Inconsistent system (no solution): The equations contradict each other (think parallel lines that never intersect). If $D = 0$ and at least one of $D_x, D_y, D_z$ is not zero, the system is inconsistent.
• Dependent system (infinitely many solutions): The equations are redundant, describing the same line or plane. If $D = 0$ and $D_x = D_y = D_z = 0$, the system may be dependent.

The critical check: Cramer's Rule only applies when $D \neq 0$. Always compute $D$ first. If it equals zero, Cramer's Rule can't solve the system, and you'll need to use another method (like Gaussian elimination) to determine whether the system is inconsistent or dependent.