2.7 Linear Inequalities and Absolute Value Inequalities

Linear Inequalities

Linear inequalities compare expressions using symbols like $<$, $>$, $\leq$, or $\geq$ instead of an equals sign. Solving them works a lot like solving equations, with one critical difference: multiplying or dividing by a negative number flips the inequality sign. The solution isn't a single number but a whole range of values, which you'll represent using interval notation and number line graphs.

Properties of Inequality Solutions

Three rules govern how you can manipulate inequalities:

• Addition/Subtraction Property: Adding or subtracting the same value on both sides keeps the inequality direction the same. If $x < 5$, then $x + 3 < 8$.
• Multiplication/Division by a Positive: Multiplying or dividing both sides by a positive number keeps the inequality direction the same. If $2x > 10$, then $x > 5$.
• Multiplication/Division by a Negative (the tricky one): Multiplying or dividing both sides by a negative number reverses the inequality. If $-3x < 9$, dividing both sides by $-3$ gives $x > -3$. The $<$ flipped to $>$.

That third rule is where most mistakes happen. Every time you divide or multiply by a negative, flip the sign.

Solving a Linear Inequality Step-by-Step

Solve $2x - 5 < 7$:

1. Add 5 to both sides: $2x < 12$
2. Divide both sides by 2 (positive, so no flip): $x < 6$

The solution is every real number less than 6.

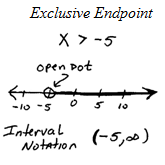
Interval Notation

Interval notation is a compact way to write solution sets. It uses:

• Parentheses $( \, )$ for endpoints that are not included (strict inequalities $<$ or $>$)
• Brackets $[ \, ]$ for endpoints that are included (non-strict inequalities $\leq$ or $\geq$)
• $\infty$ and $-\infty$ always get parentheses, since infinity isn't a reachable number

Notice that last example mixes a parenthesis on the left ($-3$ is excluded) with a bracket on the right ($4$ is included).

Graphing on a Number Line

To graph an inequality on a number line:

1. Find the boundary value by solving the inequality.
2. Draw an open circle (○) for strict inequalities ($<$ or $>$), or a closed circle (●) for non-strict inequalities ($\leq$ or $\geq$).
3. Shade the direction that satisfies the inequality. For $x < 6$, shade to the left of 6. For $x \geq -2$, shade to the right of $-2$.

Absolute Value Inequalities

The absolute value $|x|$ measures distance from zero on the number line. So absolute value inequalities are really asking: how far from zero (or some other point) can this expression be?

The key skill here is rewriting an absolute value inequality as a compound inequality without absolute value signs, then solving it like a regular inequality.

Rewriting Rules

There are two cases, and they work differently:

"Less than" type ($|x| < a$ or $|x| \leq a$): The expression inside is trapped between $-a$ and $a$. This gives you one connected interval.

"Greater than" type ($|x| > a$ or $|x| \geq a$): The expression is outside the range from $-a$ to $a$. This gives you two separate regions.

A quick way to remember: less than = "and" (between), greater than = "or" (outside).

Solving an Absolute Value Inequality Step-by-Step

Solve $|2x - 3| < 5$:

1. Identify the type: this is a "less than" inequality, so rewrite as a compound inequality: $-5 < 2x - 3 < 5$

2. Add 3 to all three parts: $-2 < 2x < 8$

3. Divide all three parts by 2: $-1 < x < 4$

4. Write in interval notation: $(-1, 4)$

Solve $|x + 1| \geq 3$:

1. Identify the type: this is a "greater than or equal to" inequality, so split into two: $x + 1 \leq -3$ or $x + 1 \geq 3$
2. Solve each separately: $x \leq -4$ or $x \geq 2$
3. Write in interval notation: $(-\infty, -4] \cup [2, \infty)$

The $\cup$ symbol means "union," combining both separate solution regions.

Special Cases to Watch For

• $|x| < 0$ has no solution, since absolute value can never be negative.
• $|x| \geq 0$ is true for all real numbers, since absolute value is always zero or positive.
• $|x| > -5$ is also true for all real numbers (same reasoning).

If you get a result that seems too simple, check whether the inequality is comparing absolute value to a negative number. That's usually what's going on.