🔦electrical circuits and systems ii review
3.4 Asymptotic approximations in Bode plots
Last Updated on August 9, 2024
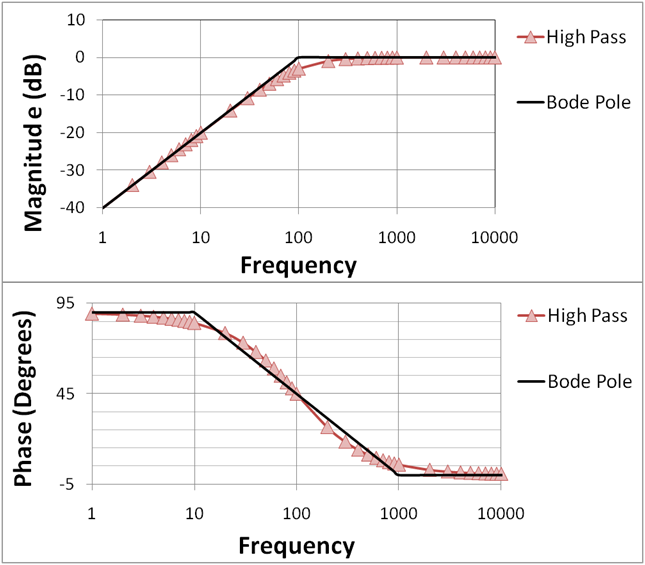
Asymptotic approximations in Bode plots simplify complex frequency responses into straight lines. This method helps us quickly estimate how systems behave at different frequencies, using logarithmic scales for magnitude and frequency.
Low and high-frequency asymptotes represent system behavior below and above the corner frequency. Understanding these asymptotes and how they connect allows us to construct Bode plots efficiently, providing valuable insights into a system's frequency response characteristics.
Low and High-Frequency Asymptotes
Understanding Asymptotic Approximations
Top images from around the web for Understanding Asymptotic Approximations
File:Bode High-Pass.PNG - Wikipedia, the free encyclopedia View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
File:Bode High-Pass.PNG - Wikipedia, the free encyclopedia View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
1 of 3
Top images from around the web for Understanding Asymptotic Approximations
File:Bode High-Pass.PNG - Wikipedia, the free encyclopedia View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
File:Bode High-Pass.PNG - Wikipedia, the free encyclopedia View original
Is this image relevant?
Bode Diagrams - Electronics-Lab.com View original
Is this image relevant?
1 of 3
- Asymptotic approximation simplifies complex frequency response curves into straight lines
- Provides quick estimation of system behavior at different frequencies
- Utilizes logarithmic scales for both magnitude and frequency
- Consists of low-frequency and high-frequency asymptotes
- Accuracy improves as frequency moves away from corner frequency
Analyzing Low and High-Frequency Behaviors
- Low-frequency asymptote represents system response at frequencies much lower than corner frequency
- Remains constant (0 dB/decade slope) for frequencies below corner frequency
- High-frequency asymptote depicts system behavior at frequencies much higher than corner frequency
- Slope depends on system order (20 dB/decade for first-order, 40 dB/decade for second-order)
- Corner frequency marks transition point between low and high-frequency regions
- Straight-line approximation connects low and high-frequency asymptotes
- Actual response curve smoothly transitions between asymptotes near corner frequency
Constructing Bode Plots with Asymptotes
- Start by plotting low-frequency asymptote as horizontal line
- Identify corner frequency (break point) where response changes
- Draw high-frequency asymptote with appropriate slope from corner frequency
- Connect asymptotes with straight line at corner frequency
- Refine approximation by adjusting curve near corner frequency (3 dB down for first-order systems)
- Use multiple asymptotes for systems with multiple poles or zeros
- Combine individual asymptotes to create overall system response
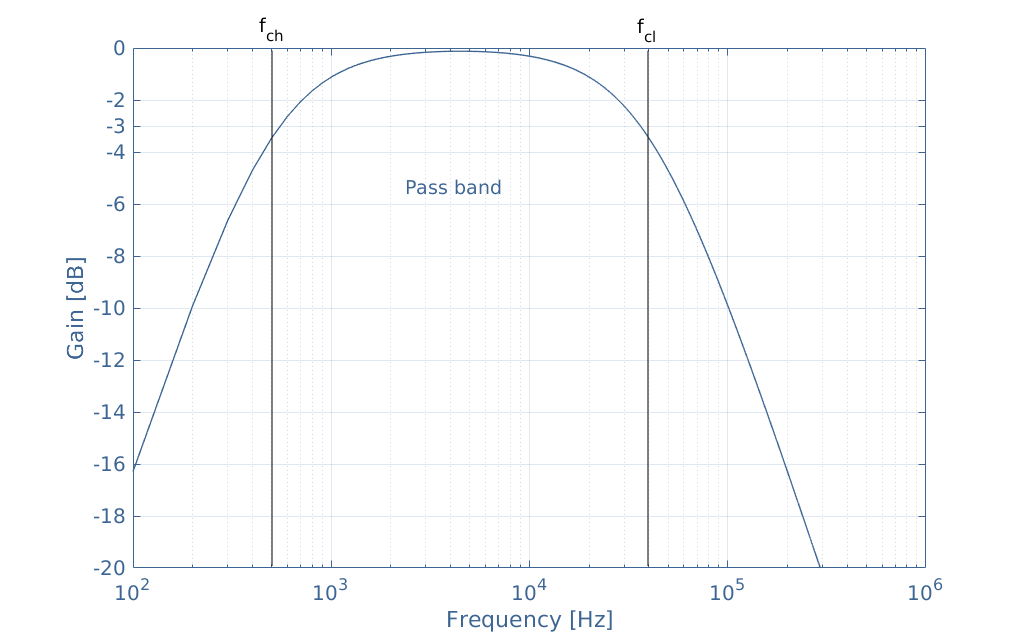
System Order and Roll-Off
Characteristics of First-Order Systems
- First-order systems contain one energy storage element (capacitor or inductor)
- Transfer function has one pole
- Low-frequency asymptote remains flat (0 dB/decade)
- High-frequency asymptote has -20 dB/decade slope
- Corner frequency occurs at where τ is the time constant
- Phase shift ranges from 0° to -90° across frequency spectrum
- Examples include RC low-pass filter, RL high-pass filter
Analyzing Second-Order Systems
- Second-order systems have two energy storage elements
- Transfer function contains two poles
- Low-frequency asymptote stays flat (0 dB/decade)
- High-frequency asymptote exhibits -40 dB/decade slope
- Two corner frequencies possible, creating more complex response
- Phase shift spans from 0° to -180° across frequency range
- Damping factor influences peak resonance and overall response shape
- Examples include RLC circuits, mechanical mass-spring-damper systems
Understanding Roll-Off Rates
- Roll-off rate measures how quickly system attenuates signals beyond corner frequency
- Expressed in dB/decade or dB/octave
- First-order systems roll off at -20 dB/decade (-6 dB/octave)
- Second-order systems roll off at -40 dB/decade (-12 dB/octave)
- Higher-order systems have steeper roll-off rates (multiples of 20 dB/decade)
- Roll-off rate affects filter sharpness and ability to separate frequencies
- Steeper roll-off improves frequency selectivity but may introduce phase distortion
Pole-Zero Cancellation
Concept and Implications of Pole-Zero Cancellation
- Occurs when a pole and zero exist at same frequency in transfer function
- Mathematically cancels out, simplifying system order
- Reduces overall system complexity and changes frequency response
- Can potentially eliminate desirable system characteristics
- May result from improper system design or component tolerances
- Affects both magnitude and phase responses of system
Effects on System Behavior and Design Considerations
- Eliminates corner frequency associated with cancelled pole-zero pair
- Changes roll-off rate by reducing effective system order
- Can improve or degrade system stability depending on cancelled dynamics
- May remove filtering effects at specific frequencies
- Requires careful analysis to ensure desired system performance is maintained
- Can be intentionally used to shape frequency response (notch filters)
- Sensitivity to component variations may lead to incomplete cancellation in practice
Key Terms to Review (21)
Negative feedback: Negative feedback is a process in control systems where the output of a system is fed back in a way that reduces the overall output. This mechanism helps stabilize systems by automatically correcting deviations from a desired level. It plays a crucial role in various applications, enabling improved accuracy and stability in performance.
First-order system: A first-order system is a dynamic system characterized by a single energy storage element and a first-order differential equation that describes its behavior. These systems respond to input changes in a predictable way, typically exhibiting exponential behavior in their response over time. The simplicity of first-order systems makes them foundational in control theory and signal processing, as they help in understanding more complex systems.
Frequency Response: Frequency response is the measure of an output signal's amplitude and phase change in response to a range of input frequencies, providing insight into how a system behaves when subjected to different signals. It helps analyze systems in terms of their stability, performance, and effectiveness in processing signals, making it crucial for understanding circuit behavior under AC conditions and its filtering characteristics.
Logarithmic scaling: Logarithmic scaling is a method of displaying data that uses logarithms to transform values, allowing for a more manageable visualization of data that spans multiple orders of magnitude. This technique is particularly useful in engineering and scientific applications, as it simplifies the representation of exponential relationships and enhances clarity when analyzing systems with wide-ranging frequency responses, such as in the case of Bode plots.
Transient response: Transient response refers to the behavior of a circuit when it is subjected to a sudden change in conditions, such as switching on a voltage or current source. This period of time is characterized by temporary fluctuations before the system settles into its steady-state condition. Understanding transient response is crucial for analyzing how circuits react immediately after disturbances, as it influences stability, performance, and how well a circuit meets design specifications.
Positive feedback: Positive feedback is a process where the output of a system amplifies its own input, leading to an increase in activity or effect within the system. This mechanism can lead to exponential growth or runaway effects, significantly influencing the behavior of electronic circuits and systems. In many cases, positive feedback can enhance performance, but it also risks instability if not controlled properly.
Roll-off rate: The roll-off rate refers to the speed at which the amplitude of a filter's frequency response decreases beyond its cutoff frequency. This term is essential for understanding how effectively a filter attenuates unwanted frequencies, which is crucial when designing circuits and analyzing systems that rely on specific frequency ranges.
Low-frequency asymptote: The low-frequency asymptote is a graphical representation in Bode plots that indicates how the gain of a system behaves as the frequency approaches zero. This aspect of the plot is crucial because it helps to predict the system's behavior at low frequencies, allowing for an understanding of system stability and performance in the desired operating range.
Second-order system: A second-order system is a dynamic system characterized by a second-degree differential equation, which typically describes how the output responds to input changes. These systems are fundamental in control theory and signal processing, exhibiting behaviors like oscillations and overshoot depending on their damping ratio and natural frequency. Understanding these characteristics is crucial for analyzing system stability and performance in various applications.
Damping Factor: The damping factor is a measure of how oscillations in a system decay after a disturbance. It quantifies the extent to which oscillations are suppressed over time, indicating how quickly a system returns to equilibrium. A higher damping factor generally means faster stabilization and less overshoot, which plays an important role in the analysis of system responses in frequency domain representations, especially in Bode plots.
High-frequency asymptote: The high-frequency asymptote refers to the behavior of a system's frequency response at very high frequencies, where the gain of the system approaches a constant value, often decreasing at a specific rate. This concept is crucial for understanding how the output of a circuit or system behaves as frequency increases and helps in predicting stability and performance in high-frequency applications.
Pole-zero plot: A pole-zero plot is a graphical representation of the poles and zeros of a transfer function in the complex frequency plane. This plot helps in understanding the behavior and stability of linear time-invariant systems by visually indicating how the locations of poles and zeros affect system dynamics, frequency response, and stability characteristics.
Phase Approximation: Phase approximation is a method used in control systems and signal processing to simplify the analysis of systems' phase responses at various frequencies. This technique enables engineers to understand how the phase of a system behaves in relation to frequency changes, particularly in the context of Bode plots. By approximating the phase response, complex systems can be analyzed more easily, allowing for insights into stability and performance without requiring extensive calculations.
Magnitude Approximation: Magnitude approximation refers to a technique used in Bode plots to simplify the representation of system frequency response. This method allows for easier analysis by approximating the gain of a transfer function as a straight line in a logarithmic scale, making it possible to visualize how the gain behaves across different frequencies without needing complex calculations.
Gain Crossover Frequency: Gain crossover frequency is the frequency at which the gain of a control system's open-loop transfer function is equal to one, or 0 dB. This frequency is crucial for understanding system stability and performance, as it marks the point where the system transitions from amplification to attenuation. Identifying this frequency helps in designing control systems that can achieve desired performance metrics, particularly in relation to stability margins and phase behavior in Bode plots.
Corner frequency: Corner frequency, often referred to as the cutoff frequency, is the frequency at which the output power of a circuit falls to half its maximum value. This concept is pivotal in understanding how systems respond to different frequencies and is crucial in the analysis and design of filters and control systems. It serves as a transition point where the system begins to attenuate signals, making it a fundamental aspect when constructing and interpreting Bode plots and making asymptotic approximations.
Intercept: In the context of electrical engineering, particularly in frequency response analysis, an intercept refers to a specific point where a curve intersects a reference axis on a graph, such as a Bode plot. Understanding the intercept is crucial for analyzing system gain and phase shift characteristics at certain frequencies, allowing for effective construction and interpretation of Bode plots, as well as making asymptotic approximations more manageable.
Slope: In the context of Bode plots, slope refers to the rate of change of the magnitude or phase of a transfer function with respect to frequency, typically expressed in decibels per decade for magnitude and degrees per decade for phase. This concept helps in understanding how the system's output responds to changes in frequency and is crucial when constructing and interpreting Bode plots. The slope indicates the system's gain characteristics and stability margins, impacting design choices and performance analysis.
Phase Margin: Phase margin is a stability criterion in control systems that indicates how much additional phase lag can be tolerated before the system becomes unstable. It represents the difference between the phase of the open-loop transfer function and -180 degrees at the gain crossover frequency, where the magnitude of the transfer function is equal to one. A higher phase margin generally indicates a more stable system.
Stability: Stability refers to the ability of a system to return to a state of equilibrium after being disturbed. In the context of control systems and circuits, stability is crucial for ensuring that systems respond predictably and do not oscillate uncontrollably or diverge over time.
Steady-state response: The steady-state response refers to the behavior of a system after transients have dissipated and the system has reached a stable output in response to a constant input. This state is crucial for analyzing how circuits respond to sinusoidal inputs, revealing their characteristics over time without the effects of initial conditions.