Heat and Mass Transfer

8.2 Numerical Methods for Unsteady-State Diffusion

Citation:

Numerical methods are essential for solving complex unsteady-state diffusion problems that defy analytical solutions. These techniques discretize space and time, approximating derivatives with finite differences and iteratively solving the resulting equations.

Finite difference methods, including explicit, implicit, and Crank-Nicolson schemes, are commonly used for diffusion problems. These methods vary in stability, accuracy, and computational efficiency, with the choice depending on problem specifics and desired solution characteristics.

Principles and limitations of numerical methods

Discretization and approximation

Numerical methods approximate solutions to complex unsteady-state diffusion problems that cannot be solved analytically
- Nonlinearities, complex geometries, or boundary conditions make analytical solutions infeasible
Principles of numerical methods involve discretizing spatial and temporal domains
- Approximating derivatives using finite differences
- Iteratively solving the resulting system of equations
Limitations of numerical methods include truncation errors introduced by discretization
- Numerical dispersion and dissipation can affect solution accuracy
- Stability issues can lead to divergence or oscillations in the solution

Accuracy and boundary conditions

Accuracy of numerical solutions depends on several factors
- Spatial and temporal resolution
- Choice of numerical scheme
- Handling of boundary conditions
Numerical methods require appropriate initial and boundary conditions to be specified
- Incorrect or poorly specified conditions can impact the solution's accuracy and stability
Higher spatial and temporal resolution generally improves accuracy but increases computational cost
Proper treatment of boundary conditions is crucial for obtaining accurate solutions
- Dirichlet (fixed value), Neumann (fixed gradient), or Robin (mixed) conditions
- Boundary conditions incorporated into the discretized equations

Finite difference methods for diffusion

Explicit and implicit methods

Finite difference methods discretize spatial and temporal domains into a grid of nodes
- Convert continuous governing equations into a system of discrete equations
Explicit finite difference method calculates future state of a node using current state of the node and its neighbors
- Simple and computationally efficient but has stability limitations
- Stability governed by the Courant-Friedrichs-Lewy (CFL) condition, limiting maximum allowable time step
Implicit finite difference method calculates future state of a node using both current and future states of the node and its neighbors
- More stable but computationally intensive
- Unconditionally stable, allowing for larger time steps without compromising stability

Crank-Nicolson method and discretization

Crank-Nicolson method is a second-order accurate, unconditionally stable finite difference scheme
- Combines explicit and implicit methods, providing a balance between accuracy and stability
- Often chosen for its ability to handle a wide range of problems effectively
Discretization of the transient diffusion equation involves approximating derivatives
- Spatial derivatives approximated using central, forward, or backward differences
- Temporal derivatives approximated using forward or backward differences
Choice of spatial and temporal step sizes affects accuracy, stability, and computational cost
- Smaller step sizes improve accuracy but increase computational expense
Boundary conditions are incorporated into the finite difference equations by modifying the discretization stencil at the domain boundaries
- Ensures the numerical solution satisfies the prescribed boundary conditions

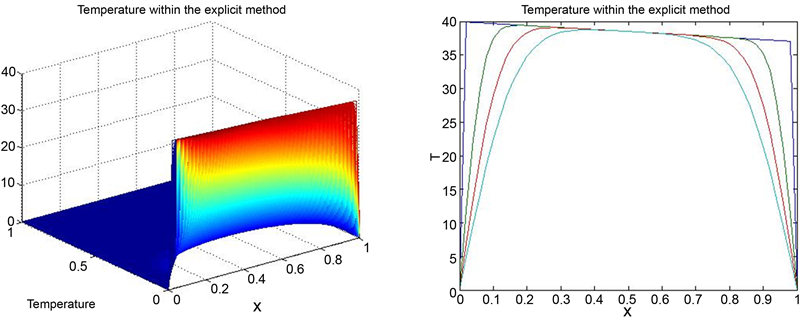
Stability, convergence, and accuracy of solutions

Stability and convergence analysis

Stability analysis determines whether the numerical solution remains bounded and does not amplify errors over time
- Ensures the solution does not diverge or exhibit spurious oscillations
Implicit finite difference methods and Crank-Nicolson method are unconditionally stable
- Allow for larger time steps without compromising stability
Convergence analysis assesses whether the numerical solution approaches the exact solution as spatial and temporal step sizes decrease
- Ensures discretization errors diminish with refinement
Order of convergence quantifies the rate at which the numerical solution converges to the exact solution
- Higher-order methods exhibit faster convergence rates (quadratic, cubic, etc.)

Accuracy assessment and error analysis

Accuracy analysis quantifies the error between the numerical solution and the exact solution
- Considers both discretization errors and round-off errors
Truncation error represents the difference between the exact derivative and its finite difference approximation
- Depends on the order of the numerical scheme and the step sizes
- Higher-order schemes have smaller truncation errors for a given step size
Grid refinement studies can be performed to assess spatial and temporal convergence
- Estimate the order of accuracy by comparing solutions at different resolutions
Richardson extrapolation can be used to improve the accuracy of numerical solutions
- Combines solutions at different step sizes to cancel out leading-order error terms

Numerical methods for transient diffusion problems

Selecting appropriate numerical methods

Choice of numerical method depends on the complexity of the problem
- Nonlinearities, variable coefficients, or complex geometries influence the selection
Explicit finite difference methods are suitable for simple problems with regular geometries and mild stability restrictions
- Offer computational efficiency and ease of implementation
Implicit finite difference methods are preferred for problems with stringent stability requirements, large time steps, or stiff systems
- Provide enhanced stability at the cost of increased computational complexity
Crank-Nicolson method is often chosen for its second-order accuracy and unconditional stability
- Strikes a balance between accuracy and stability for a wide range of problems

Handling complex problems and geometries

Handling of boundary conditions is crucial in selecting an appropriate numerical method
- Some methods may be more suitable for certain types of boundary conditions (Dirichlet, Neumann, or Robin)
For problems with complex geometries or irregular boundaries, finite element or finite volume methods may be more appropriate than finite difference methods
- These methods can better adapt to irregular domains and capture local solution features
Presence of sharp gradients, discontinuities, or singularities in the solution may require specialized numerical techniques
- Adaptive mesh refinement dynamically adjusts the grid resolution to capture solution features
- High-resolution schemes (WENO, ENO) can accurately resolve steep gradients and discontinuities
Computational cost and memory requirements of the numerical method should be considered
- Balance desired accuracy and resolution with available computational resources
Parallel computing techniques can be employed to accelerate computations for large-scale problems
- Decompose the domain into subdomains and solve them concurrently on multiple processors

Key Terms to Review (17)

Adaptive mesh refinement: Adaptive mesh refinement is a computational technique used to dynamically adjust the resolution of a mesh in numerical simulations, allowing for increased accuracy in regions with high gradients or complex features. This method optimizes computational resources by refining the mesh where it is most needed, while keeping a coarser mesh in areas where less detail is required. The goal is to enhance solution accuracy and reduce computational cost, particularly in unsteady-state diffusion problems.

Truncation error: Truncation error refers to the difference between the exact mathematical solution of a problem and the approximate solution obtained through numerical methods. It occurs when an infinite process is approximated by a finite one, often seen in the discretization of differential equations. This type of error is crucial in understanding the accuracy and stability of numerical solutions, especially when dealing with unsteady-state diffusion problems.

Discretization: Discretization is the process of transforming continuous models and equations into discrete counterparts, often by breaking down a domain into smaller, manageable sections or nodes. This technique is crucial in numerical simulations as it allows complex physical phenomena, such as heat and mass transfer, to be approximated using numerical methods. By discretizing a problem, we can apply computational techniques to solve equations that govern unsteady-state diffusion, fluid dynamics, and conduction problems.

Time step size: Time step size refers to the discrete intervals at which a numerical simulation updates its calculations for unsteady-state diffusion problems. This parameter is crucial in determining the accuracy and stability of the numerical solution, as it controls how often changes in temperature or concentration are calculated over time. A smaller time step size generally leads to more precise results but requires more computational resources, while a larger time step can speed up calculations but may compromise accuracy.

Stability criterion: The stability criterion is a mathematical condition that determines the stability of a numerical solution when modeling physical phenomena, particularly in unsteady-state diffusion and conduction problems. This criterion ensures that the numerical method produces results that converge to the true solution over time without exhibiting oscillations or divergence. It is crucial for ensuring accurate simulations and reliable predictions in transient heat and mass transfer processes.

Fourier's Law of Heat Conduction: Fourier's Law of Heat Conduction states that the heat transfer rate through a material is proportional to the negative gradient of temperature and the area through which heat is being conducted. This principle forms the foundation for analyzing how heat moves in both steady and unsteady states, allowing for calculations involving multidimensional heat flow and time-dependent temperature distributions.

Convergence analysis: Convergence analysis refers to the process of assessing whether a numerical method approaches the exact solution of a mathematical problem as the discretization parameters are refined. This concept is essential for ensuring that numerical methods yield accurate and reliable results, particularly in simulations involving unsteady-state diffusion where time and spatial discretization play a crucial role in the solution process.

Crank-Nicolson Method: The Crank-Nicolson method is a numerical technique used for solving partial differential equations, particularly useful in heat conduction and diffusion problems. It combines the features of both explicit and implicit methods, offering a stable and accurate way to handle time-dependent problems while allowing for flexibility in grid spacing. This method is especially effective for unsteady-state diffusion and conduction scenarios, enabling the calculation of temperature or concentration distributions over time.

Robin Boundary Condition: The Robin boundary condition is a type of boundary condition used in heat transfer problems that combines both Dirichlet and Neumann conditions, expressing a linear relationship between the function and its derivative at the boundary. This condition is particularly useful for modeling physical situations where heat transfer occurs through convection and conduction at the surface, effectively linking the surface temperature to the heat flux. It plays a significant role in unsteady-state diffusion problems and in multidimensional heat conduction scenarios.

Implicit scheme: An implicit scheme is a numerical method used for solving partial differential equations, especially in unsteady-state problems, where the solution at the next time step is expressed in terms of both the known and unknown values at that step. This approach allows for greater stability and accuracy in computations compared to explicit schemes, particularly when dealing with stiff equations or larger time steps. It requires solving a system of equations at each time step but is often more efficient for complex problems.

Explicit scheme: An explicit scheme is a numerical method used to solve differential equations by directly calculating the state of a system at a future time based on known information from the current state. This method updates the solution using straightforward calculations without needing iterative procedures, which makes it relatively easy to implement. However, explicit schemes are often limited by stability conditions, which can constrain the size of the time step and grid spacing used in simulations.

Uniform grid: A uniform grid is a structured arrangement of points or cells that are evenly spaced in a specific domain, often used in numerical methods for solving partial differential equations. This consistent spacing allows for simplified calculations, making it easier to apply numerical methods to model physical phenomena, such as unsteady-state diffusion. The uniform grid provides a systematic approach to discretizing a continuous problem, ensuring that the computational domain is covered without gaps or overlaps.

Finite difference method: The finite difference method is a numerical technique used to approximate solutions to differential equations by discretizing the variables involved. This method transforms continuous functions into discrete counterparts, allowing for the analysis of systems such as heat and mass transfer. It is particularly useful in solving steady-state and unsteady-state diffusion problems, as well as addressing complex inverse problems in heat and mass transfer.

Dirichlet Boundary Condition: A Dirichlet boundary condition specifies the value of a function at a boundary, typically used in heat and mass transfer problems. This type of condition ensures that the temperature or concentration at the boundary is held constant, which is crucial for accurately solving differential equations related to conduction and diffusion processes.

Neumann Boundary Condition: The Neumann boundary condition is a type of boundary condition that specifies the derivative of a function on the boundary of a domain, often representing a flux or gradient at that boundary. This condition is crucial in heat and mass transfer problems as it allows for the modeling of scenarios where there is no heat or mass flow across the boundary, or when a specific rate of transfer is prescribed, impacting how heat or mass diffuses in various systems.

Fick's Second Law: Fick's Second Law describes how the concentration of a substance changes over time due to diffusion. It builds on Fick's First Law by accounting for the time-dependent behavior of diffusing substances, making it crucial for analyzing unsteady-state diffusion situations. The law highlights that the rate of change of concentration at a point is proportional to the second spatial derivative of concentration, which connects to various diffusion scenarios in different systems.

Diffusion coefficient: The diffusion coefficient is a constant that quantifies the rate at which a substance diffuses through another medium. It provides insight into how fast particles move from areas of high concentration to areas of low concentration, and it's influenced by factors such as temperature, pressure, and the properties of the substances involved. Understanding this coefficient is crucial for analyzing processes involving mass transfer, particularly in systems where heat and mass transfer occur simultaneously.

Table of Contents

❤️‍🔥heat and mass transfer review