
1.13 Removing Discontinuities
5 min read•february 15, 2024
In this guide, we’ll be diving into the fascinating world of discontinuities. Ever looked at a graph and noticed it suddenly jumps or has holes? These are discontinuities, and sometimes, we can remove them. Let's explore how we can smooth out these mathematical speed bumps and make our functions continuous.
⭕ What are Discontinuities?
Before we patch things up, let's first understand what we're dealing with. Discontinuities occur where a function "breaks." There are three types: removable, jump, and infinite. Today, we are going to focus on removable discontinuities.
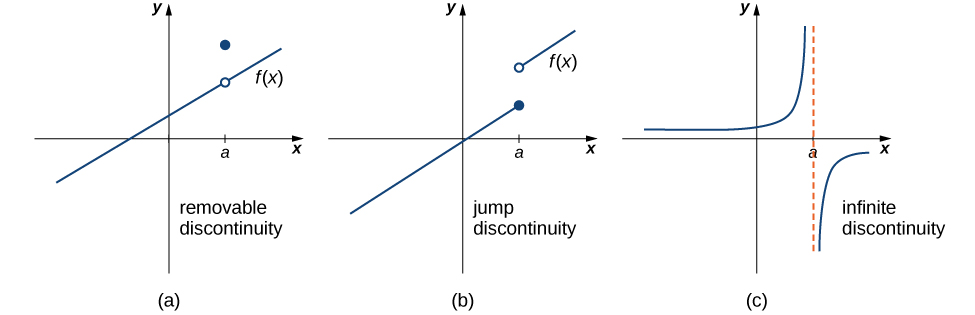
Image courtesy of LibreTexts Mathematics
📍Removable Discontinuities
Removable discontinuities are also sometimes called “holes” in a graph. They exist when a function is undefined at a point, but its limit exists. We can fill this hole to make the graph continuous. Here’s an example:
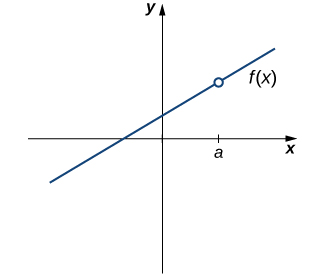
Image courtesy of LibreTexts Mathematics
We can see in this graph, the limit as approaches exists, it’s just undefined at that point. But, if we color in the circle (in other words, remove the discontinuity), the graph will be continuous over the interval in the image.
🌀 Filling the Gap
To remove a discontinuity, we redefine the function's value at that point to equal the limit of the function as x approaches that point. For example:
To remove this discontinuity, we can factor the denominator and cancel like terms, like so:
This function no longer has a discontinuity at , instead, it is defined as .
✏️ Practice Filling the Gap
Consider the function defined as follows:
where is a constant. Determine the value of that would make continuous at .
Here’s the solution! ⬇️
First, we need to factor our numerator. This will allow us to see whether we can cancel out the denominator, which is what is causing our discontinuity.
We see that there is an term in our numerator, so we can cancel it with the in the denominator!
For ,
📈 Piecewise Functions
For piecewise functions, we can ensure continuity by checking the right and left limit of the function, and assuring that the value is the same as the one defined at the point.
✔️ Ensuring Continuity
Consider defined by two pieces of a function on either side of :
- On the left side, approaches as approaches .
- On the right side, approaches as approaches .
For to be continuous at , we need .
For example, this image depicts the continuous, piecewise function
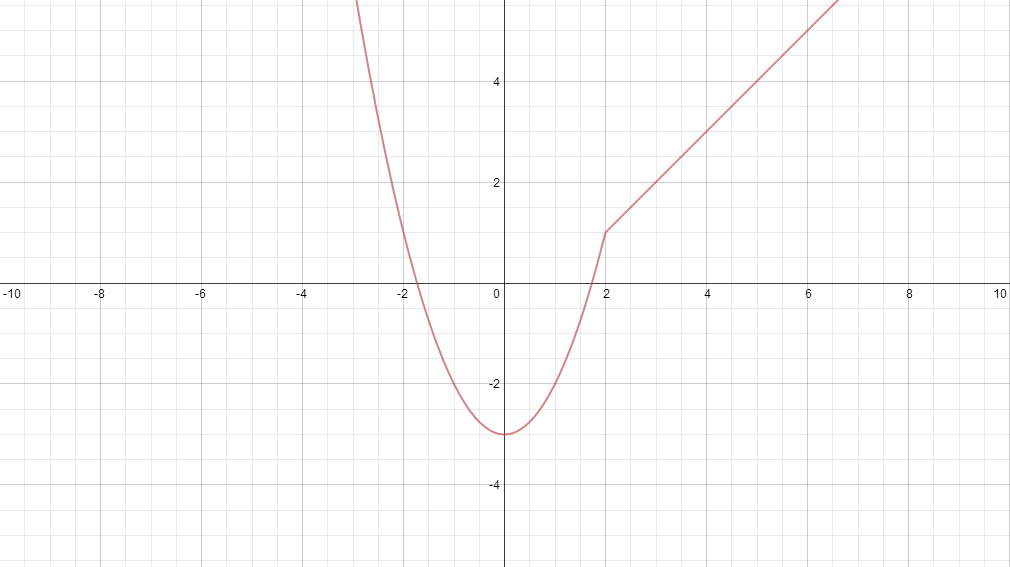
Image courtesy of mathcoachblog
We can see the the limit of as it approaches the point from the left is equal to , and similarly, from the right, it is also . Finally, is defined at as . Thus, our function is continuous.
✏️ Practice Ensuring Continuity
Consider the function,
What must be set to for the function to be continuous?
To solve this problem, we will use the first part of the piecewise function to solve for at . First, let’s factor and cancel some terms:
Now, let’s plug in :
Finally, we set this equal to and solve:
📷 Visualizing Continuity
Graphs are an excellent way to see continuity (or the lack thereof). Use graphing tools to visualize the function and identify discontinuities. A continuous graph can be drawn without lifting your pencil!
✏️ Practice Visualizing Continuity
Graph the function over the interval . Is it continuous? Can you make it continuous?
The graph of this function looks like so:
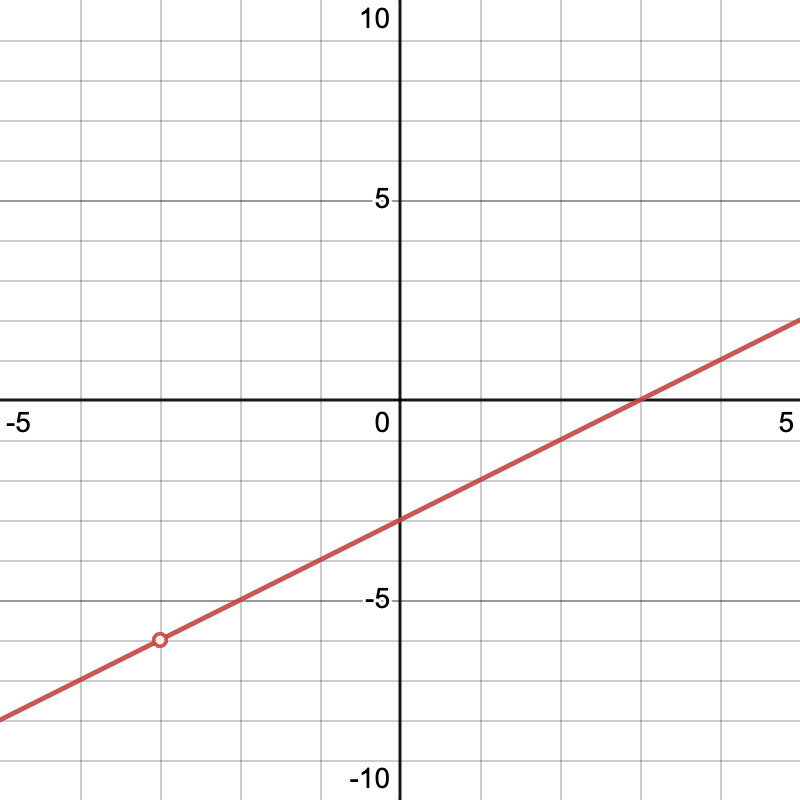
Image courtesy of Emery
You can see that there is a discontinuity at . But, we can remove it by factoring!
Plugging in , we find that at , making our function continuous.
⭐ Closing
📚 AP Calc is practice-driven! Attempt more problems, especially from past AP exams, to strengthen your understanding. Always check for continuity and practice "patching up" those functions. Great work! 👏
Key Terms to Review (12)
Continuity
: Continuity describes whether or not there are any breaks, holes, or jumps in a function. A continuous function has no interruptions and can be drawn without lifting your pen from the paper.Differentiability
: Differentiability refers to the property of a function where it has a derivative at every point in its domain. In other words, the function is smooth and has a well-defined slope at each point.Discontinuities
: Discontinuities occur when there are breaks or interruptions in the graph of a function, resulting in undefined or non-existent values at certain points.Essential Discontinuity
: An essential discontinuity occurs when there is no limit for the value of a function as it approaches a particular point, resulting in either infinite or undefined behavior.Factoring
: Factoring is the process of breaking down a mathematical expression into its simplest form by finding its factors. It involves identifying common factors and using distributive property to simplify the expression.Infinite Discontinuity
: An infinite discontinuity occurs when either one or both one-sided limits of a function approach positive or negative infinity at a certain point.Jump Discontinuity
: A jump discontinuity occurs when there is an abrupt change in the value of a function at a specific point, resulting in two separate pieces of the graph.Limit
: The limit of a function is the value that the function approaches as the input approaches a certain value or infinity. It represents the behavior of the function near a specific point.One-sided Limits
: One-sided limits are used to determine what value a function approaches from either the left side (approaching from values less than x) or right side (approaching from values greater than x). They help analyze behavior near specific points on graphs.Piecewise Functions
: Piecewise functions are functions defined by different rules for different intervals within their domain. Each rule applies to specific ranges of inputs and together they form one complete function.Rationalization
: Rationalization is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate expression. It helps simplify fractions and make them easier to work with.Removable Discontinuity
: A removable discontinuity occurs when a function has a hole at a certain point, but the limit of the function exists at that point.1.13 Removing Discontinuities
5 min read•february 15, 2024
In this guide, we’ll be diving into the fascinating world of discontinuities. Ever looked at a graph and noticed it suddenly jumps or has holes? These are discontinuities, and sometimes, we can remove them. Let's explore how we can smooth out these mathematical speed bumps and make our functions continuous.
⭕ What are Discontinuities?
Before we patch things up, let's first understand what we're dealing with. Discontinuities occur where a function "breaks." There are three types: removable, jump, and infinite. Today, we are going to focus on removable discontinuities.

Image courtesy of LibreTexts Mathematics
📍Removable Discontinuities
Removable discontinuities are also sometimes called “holes” in a graph. They exist when a function is undefined at a point, but its limit exists. We can fill this hole to make the graph continuous. Here’s an example:

Image courtesy of LibreTexts Mathematics
We can see in this graph, the limit as approaches exists, it’s just undefined at that point. But, if we color in the circle (in other words, remove the discontinuity), the graph will be continuous over the interval in the image.
🌀 Filling the Gap
To remove a discontinuity, we redefine the function's value at that point to equal the limit of the function as x approaches that point. For example:
To remove this discontinuity, we can factor the denominator and cancel like terms, like so:
This function no longer has a discontinuity at , instead, it is defined as .
✏️ Practice Filling the Gap
Consider the function defined as follows:
where is a constant. Determine the value of that would make continuous at .
Here’s the solution! ⬇️
First, we need to factor our numerator. This will allow us to see whether we can cancel out the denominator, which is what is causing our discontinuity.
We see that there is an term in our numerator, so we can cancel it with the in the denominator!
For ,
📈 Piecewise Functions
For piecewise functions, we can ensure continuity by checking the right and left limit of the function, and assuring that the value is the same as the one defined at the point.
✔️ Ensuring Continuity
Consider defined by two pieces of a function on either side of :
- On the left side, approaches as approaches .
- On the right side, approaches as approaches .
For to be continuous at , we need .
For example, this image depicts the continuous, piecewise function

Image courtesy of mathcoachblog
We can see the the limit of as it approaches the point from the left is equal to , and similarly, from the right, it is also . Finally, is defined at as . Thus, our function is continuous.
✏️ Practice Ensuring Continuity
Consider the function,
What must be set to for the function to be continuous?
To solve this problem, we will use the first part of the piecewise function to solve for at . First, let’s factor and cancel some terms:
Now, let’s plug in :
Finally, we set this equal to and solve:
📷 Visualizing Continuity
Graphs are an excellent way to see continuity (or the lack thereof). Use graphing tools to visualize the function and identify discontinuities. A continuous graph can be drawn without lifting your pencil!
✏️ Practice Visualizing Continuity
Graph the function over the interval . Is it continuous? Can you make it continuous?
The graph of this function looks like so:

Image courtesy of Emery
You can see that there is a discontinuity at . But, we can remove it by factoring!
Plugging in , we find that at , making our function continuous.
⭐ Closing
📚 AP Calc is practice-driven! Attempt more problems, especially from past AP exams, to strengthen your understanding. Always check for continuity and practice "patching up" those functions. Great work! 👏
Key Terms to Review (12)
Continuity
: Continuity describes whether or not there are any breaks, holes, or jumps in a function. A continuous function has no interruptions and can be drawn without lifting your pen from the paper.Differentiability
: Differentiability refers to the property of a function where it has a derivative at every point in its domain. In other words, the function is smooth and has a well-defined slope at each point.Discontinuities
: Discontinuities occur when there are breaks or interruptions in the graph of a function, resulting in undefined or non-existent values at certain points.Essential Discontinuity
: An essential discontinuity occurs when there is no limit for the value of a function as it approaches a particular point, resulting in either infinite or undefined behavior.Factoring
: Factoring is the process of breaking down a mathematical expression into its simplest form by finding its factors. It involves identifying common factors and using distributive property to simplify the expression.Infinite Discontinuity
: An infinite discontinuity occurs when either one or both one-sided limits of a function approach positive or negative infinity at a certain point.Jump Discontinuity
: A jump discontinuity occurs when there is an abrupt change in the value of a function at a specific point, resulting in two separate pieces of the graph.Limit
: The limit of a function is the value that the function approaches as the input approaches a certain value or infinity. It represents the behavior of the function near a specific point.One-sided Limits
: One-sided limits are used to determine what value a function approaches from either the left side (approaching from values less than x) or right side (approaching from values greater than x). They help analyze behavior near specific points on graphs.Piecewise Functions
: Piecewise functions are functions defined by different rules for different intervals within their domain. Each rule applies to specific ranges of inputs and together they form one complete function.Rationalization
: Rationalization is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate expression. It helps simplify fractions and make them easier to work with.Removable Discontinuity
: A removable discontinuity occurs when a function has a hole at a certain point, but the limit of the function exists at that point.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.