
5.1 Using the Mean Value Theorem
4 min read•february 15, 2024
In the previous unit, we learned all about applying derivatives to different real-world contexts. What else are derivatives useful for? Turns out, we can also use derivatives to determine and analyze the behaviors of functions! 👀
📈 Mean Value Theorem
The Mean Value Theorem states that if a function f is continuous over the interval and differentiable over the interval , then there exists a point within that open interval where the instantaneous rate of change of the function at equals the average rate of change of the function over the interval .
In other words, if a function f is continuous over the interval and differentiable over the interval , there exists some on such that .

Image Courtesy of Sumi Vora and Ethan Bilderbeek
Yet another way to phrase this theorem is that if the stated conditions of continuity and differentiability are satisfied, there is a point where the slope of the tangent line is equivalent to the slope of the secant line between and .
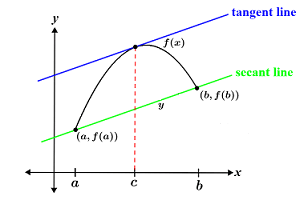
Image Courtesy of Math.net
Remember from Unit 1, to be continuous over means that there are no holes, asymptotes, or jump discontinuities between points a and b. Because the interval contains closed brackets, the graph must also be continuous at points and .
Additionally, if we recall from previous guides, to be differentiable over means that the function is continuous over the interval and that for any point over the interval, exists.
✏️ Mean Value Theorem: Walkthrough
We can use the Mean Value Theorem to justify conclusions about functions by applying it over an interval. For example:
Let be a differentiable function. The table gives its selected values:
Can we use the Mean Value Theorem to say the equation has a solution where ?
Since it is given that is differentiable, we can apply the Mean Value Theorem (MVT) on the interval . This is what we should write out!
Since is continuous and differentiable on , MVT can be applied. The MVT states that there exists a on such that
so MVT cannot be used to say that has a solution.
📝 Mean Value Theorem: Practice Problems
Now, it’s time for you to do some practice on your own! 🍀
❓ Mean Value Theorem: Practice
Question 1: Mean Value Theorem
Let and let be the number that satisfies the Mean Value Theorem for on the interval .
What is
Question 2: Mean Value Theorem
Let be a differentiable function. The table gives its selected values:
Can we use the Mean Value Theorem to say the equation has a solution where ?
✅ Mean Value Theorem: Answers and Solutions
Question 1: Mean Value Theorem
Since is a polynomial, is continuous on and differentiable on . Therefore, the Mean Value Theorem can be applied. By the Mean Value Theorem, there exists a on such that…
To find , we need to differentiate and find such that
By the quadratic formula, we have .
Since only is in the interval , Great work! Make sure you remember to check if the value(s) you get are in the given interval.
Question 2: Mean Value Theorem
Since it is given that is differentiable, we can apply the Mean Value Theorem (MVT) on the interval .
The MVT states that there exists a on such that so MVT cannot be used to say that has a solution.
💫 Closing
The Mean Value Theorem states that for any continuous function on a closed interval, there exists a value c in the interval such that the value of the derivative of the function at c is equal to the average rate of change of the function over the interval. By using this theorem, we can find the mean value of a function on a given interval, which can provide useful information about the behavior of the function. 🧐
Key Terms to Review (15)
Absolute Value Function
: The absolute value function is a mathematical function that gives the distance of a number from zero on the number line. It returns the positive value of any given input.Average Rate of Change
: The average rate of change calculates how much one variable changes in relation to another variable over an interval. It measures the slope or steepness between two points on a graph.Closed Interval
: A closed interval is a set of real numbers that includes both of its endpoints. It is denoted by square brackets [ ].Continuous
: A function is continuous if there are no breaks, jumps, or holes in its graph. In other words, you can draw the graph of a continuous function without lifting your pencil.Corner
: In calculus, a corner refers to a point on the graph of a function where two distinct lines meet, forming an angle greater than 180 degrees.Derivative
: A derivative represents the rate at which a function is changing at any given point. It measures how sensitive one quantity is to small changes in another quantity.Differentiable
: A function is differentiable if it has a derivative at every point in its domain. This means that you can find the slope of the tangent line at any point on its graph.f'(c) = [f(b)-f(a)]/b-a
: This formula represents the average rate of change (slope) between two points on a curve or graph. It calculates how much y changes per unit change in x over an interval [a,b].Instantaneous Rate of Change
: The instantaneous rate of change refers to the rate at which a function is changing at a specific point. It measures how quickly the output of a function is changing with respect to the input at that particular instant.lim x->a [f(x) - f(a)]/(x - a)
: The limit expression "lim x->a [f(x) - f(a)]/(x - a)" represents how a function approaches a specific value (a) as x gets arbitrarily close to that value.Mean Value Theorem
: The Mean Value Theorem states that if a function is continuous on a closed interval [a, b] and differentiable on an open interval (a, b), then there exists at least one point c in (a, b) where the instantaneous rate of change (derivative) equals the average rate of change over the interval.Open Interval
: An open interval is a set of real numbers between two endpoints, where the endpoints are not included in the interval.Rolle's Theorem
: Rolle's Theorem states that if a function is continuous on a closed interval [a, b], differentiable on an open interval (a, b), and has equal values for its endpoints, then there exists at least one point c in (a, b) where the derivative equals zero.Secant Line
: A secant line is a straight line that intersects a curve at two points. It represents the average rate of change between those two points on the curve.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.5.1 Using the Mean Value Theorem
4 min read•february 15, 2024
In the previous unit, we learned all about applying derivatives to different real-world contexts. What else are derivatives useful for? Turns out, we can also use derivatives to determine and analyze the behaviors of functions! 👀
📈 Mean Value Theorem
The Mean Value Theorem states that if a function f is continuous over the interval and differentiable over the interval , then there exists a point within that open interval where the instantaneous rate of change of the function at equals the average rate of change of the function over the interval .
In other words, if a function f is continuous over the interval and differentiable over the interval , there exists some on such that .

Image Courtesy of Sumi Vora and Ethan Bilderbeek
Yet another way to phrase this theorem is that if the stated conditions of continuity and differentiability are satisfied, there is a point where the slope of the tangent line is equivalent to the slope of the secant line between and .

Image Courtesy of Math.net
Remember from Unit 1, to be continuous over means that there are no holes, asymptotes, or jump discontinuities between points a and b. Because the interval contains closed brackets, the graph must also be continuous at points and .
Additionally, if we recall from previous guides, to be differentiable over means that the function is continuous over the interval and that for any point over the interval, exists.
✏️ Mean Value Theorem: Walkthrough
We can use the Mean Value Theorem to justify conclusions about functions by applying it over an interval. For example:
Let be a differentiable function. The table gives its selected values:
Can we use the Mean Value Theorem to say the equation has a solution where ?
Since it is given that is differentiable, we can apply the Mean Value Theorem (MVT) on the interval . This is what we should write out!
Since is continuous and differentiable on , MVT can be applied. The MVT states that there exists a on such that
so MVT cannot be used to say that has a solution.
📝 Mean Value Theorem: Practice Problems
Now, it’s time for you to do some practice on your own! 🍀
❓ Mean Value Theorem: Practice
Question 1: Mean Value Theorem
Let and let be the number that satisfies the Mean Value Theorem for on the interval .
What is
Question 2: Mean Value Theorem
Let be a differentiable function. The table gives its selected values:
Can we use the Mean Value Theorem to say the equation has a solution where ?
✅ Mean Value Theorem: Answers and Solutions
Question 1: Mean Value Theorem
Since is a polynomial, is continuous on and differentiable on . Therefore, the Mean Value Theorem can be applied. By the Mean Value Theorem, there exists a on such that…
To find , we need to differentiate and find such that
By the quadratic formula, we have .
Since only is in the interval , Great work! Make sure you remember to check if the value(s) you get are in the given interval.
Question 2: Mean Value Theorem
Since it is given that is differentiable, we can apply the Mean Value Theorem (MVT) on the interval .
The MVT states that there exists a on such that so MVT cannot be used to say that has a solution.
💫 Closing
The Mean Value Theorem states that for any continuous function on a closed interval, there exists a value c in the interval such that the value of the derivative of the function at c is equal to the average rate of change of the function over the interval. By using this theorem, we can find the mean value of a function on a given interval, which can provide useful information about the behavior of the function. 🧐
Key Terms to Review (15)
Absolute Value Function
: The absolute value function is a mathematical function that gives the distance of a number from zero on the number line. It returns the positive value of any given input.Average Rate of Change
: The average rate of change calculates how much one variable changes in relation to another variable over an interval. It measures the slope or steepness between two points on a graph.Closed Interval
: A closed interval is a set of real numbers that includes both of its endpoints. It is denoted by square brackets [ ].Continuous
: A function is continuous if there are no breaks, jumps, or holes in its graph. In other words, you can draw the graph of a continuous function without lifting your pencil.Corner
: In calculus, a corner refers to a point on the graph of a function where two distinct lines meet, forming an angle greater than 180 degrees.Derivative
: A derivative represents the rate at which a function is changing at any given point. It measures how sensitive one quantity is to small changes in another quantity.Differentiable
: A function is differentiable if it has a derivative at every point in its domain. This means that you can find the slope of the tangent line at any point on its graph.f'(c) = [f(b)-f(a)]/b-a
: This formula represents the average rate of change (slope) between two points on a curve or graph. It calculates how much y changes per unit change in x over an interval [a,b].Instantaneous Rate of Change
: The instantaneous rate of change refers to the rate at which a function is changing at a specific point. It measures how quickly the output of a function is changing with respect to the input at that particular instant.lim x->a [f(x) - f(a)]/(x - a)
: The limit expression "lim x->a [f(x) - f(a)]/(x - a)" represents how a function approaches a specific value (a) as x gets arbitrarily close to that value.Mean Value Theorem
: The Mean Value Theorem states that if a function is continuous on a closed interval [a, b] and differentiable on an open interval (a, b), then there exists at least one point c in (a, b) where the instantaneous rate of change (derivative) equals the average rate of change over the interval.Open Interval
: An open interval is a set of real numbers between two endpoints, where the endpoints are not included in the interval.Rolle's Theorem
: Rolle's Theorem states that if a function is continuous on a closed interval [a, b], differentiable on an open interval (a, b), and has equal values for its endpoints, then there exists at least one point c in (a, b) where the derivative equals zero.Secant Line
: A secant line is a straight line that intersects a curve at two points. It represents the average rate of change between those two points on the curve.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.