
Quantitative / Qualitative Translation
6 min read•november 2, 2020
Peter Apps
Peter Apps
The Qualitative / Quantitative Translation is one of the 5 FRQs that appear on the AP Physics 1 Exam. This particular question is usually worth 12 points (out of a total of 45) and is suggested to take around 25 minutes to complete. The word qualitative implies the use of words. The word quantitative implies the use of mathematics. This means that a QQT is a question that requires you to go between words and mathematics in describing and analyzing a situation.
What you might be asked to do on a QQT
Work with multiple representations - You may be given one representation of a situation and asked to create another representation of the same situation. Representations can include math equations, word descriptions, graphs, diagrams, and data tables.
Evaluate a student’s words - You will be presented with a situation, a question, and one or two students’ answers or arguments over what the answer is. You will be asked to break down their reasoning, identifying each feature that is correct or incorrect. Sometimes you will have to connect the correct (or incorrect) features of arguments to physics principles or equations. After figuring out what is right and wrong, you may be asked to construct a completely correct argument based on the “rights” and “wrongs” you found. Evaluate a student’s representations - You may be shown a student’s graph or work that describes the situation, but there may be features of the graph or equation that are wrong. You will need to identify the correct or incorrect features of the graph. You may be asked to then create a correct version of their representation.
What to look for:
Things to look for when evaluating a graph:
Does it have a slope (positive/negative/zero) that makes sense?
Ex. An object that is moving in the positive direction and speeding up should have a positive slope
Does it have an intercept (on the y-axis or x-axis or none at all) that makes sense?
Ex. A Period vs Length graph for a pendulum should have a 0,0 intercept.
Ex. A velocity vs time graph should have a y-intercept equal to the initial velocity
Should the graph be a line or a curve?
Is the relationship linear (Fs = kx) or quadratic (Us = 1/2kx^2)?
Things to look for when evaluating equations:
The symbols in the numerator - when they increase, does the quantity of interest increase?
The symbols in the denominator - when they increase, does the quantity of interest decrease?
Should a variable be inversely (one decreases if another increases, y=k/x) or directly related (one increases if another increases, y=1/2ax^2)?
Things to look for when evaluating a student’s words:
If the student uses proportional reasoning (sounds like this: “if the speed of a car doubles, then it has twice the energy”) check the equation that shows this relationship (in this case, K = 1/2mv^2) and see if there is actually a direct relationship (in this case, no it's a quadratic relationship). You would need to correct the student on this (it's actually four times the energy).
If the student says that something increases or decreases (sounds like this: “if the ball moves faster, then the time it takes to pass through the photogate increases”), check to see if that makes sense (“no it doesn’t—a faster ball would spend less time passing through a photogate). Get ready to correct the student’s wrong reasoning.
Sample Problem #1


The student should aim to the right of point C. In order to change the angular speed of the rod, a torque needs to be applied to it. The amount of torque depends on the force and the distance from the pivot. Increasing the distance from the pivot increases the torque which will increase the angular speed.

This equation agrees with my reasoning in part (a). If the distance from the pivot (x) is increased the angular speed 𝜔 increases as well.
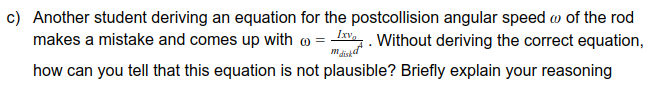
This equation shows that increasing the mass of the disk would result in a slower angular speed because mdisk is in the denominator. But a more massive disk has more angular momentum to transfer to the rod and should result in a larger angular speed. Also, a larger moment of inertia I makes the rod more difficult to rotate and should give a smaller angular speed not a larger one, so I should be in the denominator not the numerator.

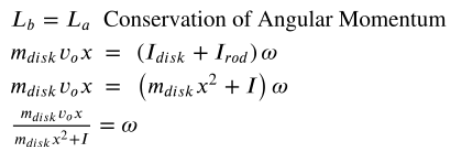

The disk bouncing off the rod has a larger change in angular momentum than when it sticks to the rod. This results in a larger angular speed in the rod afterwards because the total angular momentum of the rod-disk system has to remain constant.
Sample Problem #2
(From National Math + Science Initiative)

Two cases are shown:
Case 1 in which the block on the table is initially moving to the right, and Case 2 in which the block on the table is initially moving to the left. The two students are arguing over which case has greater acceleration and which case has greater tension in the string.
Student X: “Both cases have the same hanging mass, so both cases have the same net force on the two-block system. Both cases have the same mass on the table, so both cases have the same frictional force on the table block. If both cases have the same forces and the same masses, they must have the same accelerations and the same tensions.”
Student Y: “But you are not taking into account the direction of the friction force. In Case 1, the friction and hanging weight forces work together to create a greater net force than in Case 2. A greater net force means a greater acceleration in Case 1. If the acceleration is greater, then the tension pulling the block on the table must be greater in Case 1 as well.”
i. Which aspects of Student X’s reasoning are correct? Explain why they are correct.
Student X correctly states that both cases have the same hanging mass (shown in diagram), same force of friction on the table (Same mass on the table and same coefficient of friction, so Ff = 𝜇Fn will be the same) ii. Which aspects of Student X’s reasoning are incorrect? Explain why they are wrong.
The forces between the 2 trials are not the same. In case 1 the frictional force and the weight of the hanging block are in the same direction (right / down) and result in a larger net force. This leads to a larger acceleration for case 1. The tension on the string in case 1 is smaller, since the acceleration is greater for the hanging block (mg-T=ma) In case 2, the frictional force is to the left and is opposing the weight of the hanging block, which gives a smaller net force and acceleration. The tension is greater in case 2 as well. iii. Which aspects of Student Y’s reasoning are correct? Explain why they are correct.
Student Y correctly states that the frictional force changes direction (opposes the motion of the blocks) which gives a greater net force & acceleration in Case 1 (see reasoning in part ii for more detailed explanation) iv. Which aspects of Student Y’s reasoning are incorrect? Explain why they are wrong
Greater acceleration doesn't mean greater tension in the cord. In fact the opposite is true. Looking just at the hanging block, we can derive a Newton's 2nd Law equation to show this.
F = ma
mg - T = ma
T = mg - ma <-- a larger acceleration means a smaller tension!
Key Terms to Review (21)
Angular momentum
: Angular momentum refers to the rotational equivalent of linear momentum. It describes how fast an object rotates around an axis and depends on its mass distribution and rotational speed.Angular speed (𝜔)
: Angular speed represents how quickly an object rotates around its axis. It is measured in radians per second (rad/s).Data tables
: Data tables organize information systematically by presenting it in rows and columns. They allow us to record and compare data values efficiently.Diagrams
: Diagrams are visual representations used to illustrate concepts or processes. They often include labeled parts or steps, helping us understand complex ideas more easily.Equations
: Equations are mathematical expressions that represent relationships between different variables. In physics, equations are used to describe various physical phenomena and solve problems.Graphs
: Graphs are visual representations of data that show the relationship between variables. They use axes to plot points or lines, allowing us to analyze patterns and trends.Kinetic energy (K = 1/2mv^2)
: Kinetic energy is the energy an object possesses due to its motion. It depends on both mass and velocity and can be calculated using the formula K = 1/2mv^2.Linear relationship
: A linear relationship describes two variables that have an equal rate of change and can be represented by drawing straight lines when plotted on a graph.Moment of inertia (I)
: Moment of inertia refers to how resistant an object is to changes in its rotational motion. It depends on both mass distribution and shape.Net Force
: The net force is the overall force acting on an object, taking into account both magnitude and direction. It determines the object's acceleration or deceleration.Normal force (Fn)
: The normal force is the force exerted by a surface to support the weight of an object resting on it. It acts perpendicular to the surface.Photogate
: A photogate is an electronic sensor that uses light beams to detect objects passing through it and measures their speed or time.Physics principles
: Physics principles are fundamental concepts and laws that explain the behavior of matter and energy in the universe. They provide a framework for understanding and predicting physical phenomena.Pivot Point
: The pivot point is the fixed point around which an object rotates or turns.Proportional reasoning
: Proportional reasoning refers to the ability to understand and solve problems involving proportional relationships, where one quantity changes in direct proportion to another quantity.Quadratic relationship
: A quadratic relationship is a mathematical relationship between two variables that can be represented by a quadratic equation, where the variable is raised to the power of 2.Qualitative / Quantitative Translation
: Qualitative / Quantitative Translation refers to the process of converting information from a qualitative description to a quantitative representation or vice versa. It involves expressing observations or data in either descriptive or numerical form.Slope
: Slope refers to the steepness or incline of a line on a graph. It represents how much one variable changes with respect to another variable.Torque
: Torque refers to the measure of how effectively a force can cause an object to rotate around a fixed axis. It depends on both the magnitude and direction of the applied force.X-intercept
: The x-intercept is the point where a line crosses or intersects the x-axis on a graph.Y-intercept
: The y-intercept is the point where a line crosses or intersects the y-axis on a graph.Quantitative / Qualitative Translation
6 min read•november 2, 2020
Peter Apps
Peter Apps
The Qualitative / Quantitative Translation is one of the 5 FRQs that appear on the AP Physics 1 Exam. This particular question is usually worth 12 points (out of a total of 45) and is suggested to take around 25 minutes to complete. The word qualitative implies the use of words. The word quantitative implies the use of mathematics. This means that a QQT is a question that requires you to go between words and mathematics in describing and analyzing a situation.
What you might be asked to do on a QQT
Work with multiple representations - You may be given one representation of a situation and asked to create another representation of the same situation. Representations can include math equations, word descriptions, graphs, diagrams, and data tables.
Evaluate a student’s words - You will be presented with a situation, a question, and one or two students’ answers or arguments over what the answer is. You will be asked to break down their reasoning, identifying each feature that is correct or incorrect. Sometimes you will have to connect the correct (or incorrect) features of arguments to physics principles or equations. After figuring out what is right and wrong, you may be asked to construct a completely correct argument based on the “rights” and “wrongs” you found. Evaluate a student’s representations - You may be shown a student’s graph or work that describes the situation, but there may be features of the graph or equation that are wrong. You will need to identify the correct or incorrect features of the graph. You may be asked to then create a correct version of their representation.
What to look for:
Things to look for when evaluating a graph:
Does it have a slope (positive/negative/zero) that makes sense?
Ex. An object that is moving in the positive direction and speeding up should have a positive slope
Does it have an intercept (on the y-axis or x-axis or none at all) that makes sense?
Ex. A Period vs Length graph for a pendulum should have a 0,0 intercept.
Ex. A velocity vs time graph should have a y-intercept equal to the initial velocity
Should the graph be a line or a curve?
Is the relationship linear (Fs = kx) or quadratic (Us = 1/2kx^2)?
Things to look for when evaluating equations:
The symbols in the numerator - when they increase, does the quantity of interest increase?
The symbols in the denominator - when they increase, does the quantity of interest decrease?
Should a variable be inversely (one decreases if another increases, y=k/x) or directly related (one increases if another increases, y=1/2ax^2)?
Things to look for when evaluating a student’s words:
If the student uses proportional reasoning (sounds like this: “if the speed of a car doubles, then it has twice the energy”) check the equation that shows this relationship (in this case, K = 1/2mv^2) and see if there is actually a direct relationship (in this case, no it's a quadratic relationship). You would need to correct the student on this (it's actually four times the energy).
If the student says that something increases or decreases (sounds like this: “if the ball moves faster, then the time it takes to pass through the photogate increases”), check to see if that makes sense (“no it doesn’t—a faster ball would spend less time passing through a photogate). Get ready to correct the student’s wrong reasoning.
Sample Problem #1


The student should aim to the right of point C. In order to change the angular speed of the rod, a torque needs to be applied to it. The amount of torque depends on the force and the distance from the pivot. Increasing the distance from the pivot increases the torque which will increase the angular speed.

This equation agrees with my reasoning in part (a). If the distance from the pivot (x) is increased the angular speed 𝜔 increases as well.
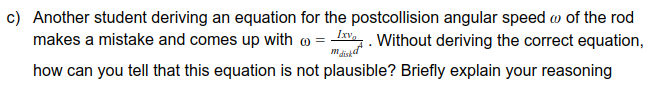
This equation shows that increasing the mass of the disk would result in a slower angular speed because mdisk is in the denominator. But a more massive disk has more angular momentum to transfer to the rod and should result in a larger angular speed. Also, a larger moment of inertia I makes the rod more difficult to rotate and should give a smaller angular speed not a larger one, so I should be in the denominator not the numerator.

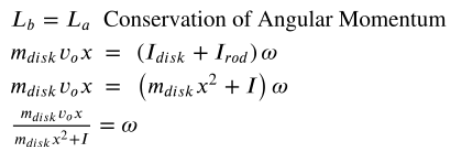

The disk bouncing off the rod has a larger change in angular momentum than when it sticks to the rod. This results in a larger angular speed in the rod afterwards because the total angular momentum of the rod-disk system has to remain constant.
Sample Problem #2
(From National Math + Science Initiative)

Two cases are shown:
Case 1 in which the block on the table is initially moving to the right, and Case 2 in which the block on the table is initially moving to the left. The two students are arguing over which case has greater acceleration and which case has greater tension in the string.
Student X: “Both cases have the same hanging mass, so both cases have the same net force on the two-block system. Both cases have the same mass on the table, so both cases have the same frictional force on the table block. If both cases have the same forces and the same masses, they must have the same accelerations and the same tensions.”
Student Y: “But you are not taking into account the direction of the friction force. In Case 1, the friction and hanging weight forces work together to create a greater net force than in Case 2. A greater net force means a greater acceleration in Case 1. If the acceleration is greater, then the tension pulling the block on the table must be greater in Case 1 as well.”
i. Which aspects of Student X’s reasoning are correct? Explain why they are correct.
Student X correctly states that both cases have the same hanging mass (shown in diagram), same force of friction on the table (Same mass on the table and same coefficient of friction, so Ff = 𝜇Fn will be the same) ii. Which aspects of Student X’s reasoning are incorrect? Explain why they are wrong.
The forces between the 2 trials are not the same. In case 1 the frictional force and the weight of the hanging block are in the same direction (right / down) and result in a larger net force. This leads to a larger acceleration for case 1. The tension on the string in case 1 is smaller, since the acceleration is greater for the hanging block (mg-T=ma) In case 2, the frictional force is to the left and is opposing the weight of the hanging block, which gives a smaller net force and acceleration. The tension is greater in case 2 as well. iii. Which aspects of Student Y’s reasoning are correct? Explain why they are correct.
Student Y correctly states that the frictional force changes direction (opposes the motion of the blocks) which gives a greater net force & acceleration in Case 1 (see reasoning in part ii for more detailed explanation) iv. Which aspects of Student Y’s reasoning are incorrect? Explain why they are wrong
Greater acceleration doesn't mean greater tension in the cord. In fact the opposite is true. Looking just at the hanging block, we can derive a Newton's 2nd Law equation to show this.
F = ma
mg - T = ma
T = mg - ma <-- a larger acceleration means a smaller tension!
Key Terms to Review (21)
Angular momentum
: Angular momentum refers to the rotational equivalent of linear momentum. It describes how fast an object rotates around an axis and depends on its mass distribution and rotational speed.Angular speed (𝜔)
: Angular speed represents how quickly an object rotates around its axis. It is measured in radians per second (rad/s).Data tables
: Data tables organize information systematically by presenting it in rows and columns. They allow us to record and compare data values efficiently.Diagrams
: Diagrams are visual representations used to illustrate concepts or processes. They often include labeled parts or steps, helping us understand complex ideas more easily.Equations
: Equations are mathematical expressions that represent relationships between different variables. In physics, equations are used to describe various physical phenomena and solve problems.Graphs
: Graphs are visual representations of data that show the relationship between variables. They use axes to plot points or lines, allowing us to analyze patterns and trends.Kinetic energy (K = 1/2mv^2)
: Kinetic energy is the energy an object possesses due to its motion. It depends on both mass and velocity and can be calculated using the formula K = 1/2mv^2.Linear relationship
: A linear relationship describes two variables that have an equal rate of change and can be represented by drawing straight lines when plotted on a graph.Moment of inertia (I)
: Moment of inertia refers to how resistant an object is to changes in its rotational motion. It depends on both mass distribution and shape.Net Force
: The net force is the overall force acting on an object, taking into account both magnitude and direction. It determines the object's acceleration or deceleration.Normal force (Fn)
: The normal force is the force exerted by a surface to support the weight of an object resting on it. It acts perpendicular to the surface.Photogate
: A photogate is an electronic sensor that uses light beams to detect objects passing through it and measures their speed or time.Physics principles
: Physics principles are fundamental concepts and laws that explain the behavior of matter and energy in the universe. They provide a framework for understanding and predicting physical phenomena.Pivot Point
: The pivot point is the fixed point around which an object rotates or turns.Proportional reasoning
: Proportional reasoning refers to the ability to understand and solve problems involving proportional relationships, where one quantity changes in direct proportion to another quantity.Quadratic relationship
: A quadratic relationship is a mathematical relationship between two variables that can be represented by a quadratic equation, where the variable is raised to the power of 2.Qualitative / Quantitative Translation
: Qualitative / Quantitative Translation refers to the process of converting information from a qualitative description to a quantitative representation or vice versa. It involves expressing observations or data in either descriptive or numerical form.Slope
: Slope refers to the steepness or incline of a line on a graph. It represents how much one variable changes with respect to another variable.Torque
: Torque refers to the measure of how effectively a force can cause an object to rotate around a fixed axis. It depends on both the magnitude and direction of the applied force.X-intercept
: The x-intercept is the point where a line crosses or intersects the x-axis on a graph.Y-intercept
: The y-intercept is the point where a line crosses or intersects the y-axis on a graph.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.