
What is a Limit?
3 min read•october 28, 2020
Rupi Adhikary
Rupi Adhikary
What is a limit?
A limit denotes the behavior of a function as it approaches a certain value which is especially important in calculus. In mathematical terms, the limit is asking the question "What value is 'y' getting close to as 'x' approaches a number?" and its represented by the expression:
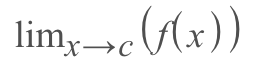
Out loud, this would sound something like "the limit of f(x) as x approaches c"
- The 'lim' shows that we're finding the limit and not the value of the function
- The 'x →c' tells us the value that x is getting closer and closer to but never actually reaching
- The 'f(x)' is meant to represent the functions you're working with
🎥Live Stream Replay: Algebraic Limits
Three Criteria for Limits to Exist
Study Guide: Determining Procedures for Determining Limits
1.) The limit of the function approaching from the right exists
- Graphically, this would look like following a function to a certain point on the x-axis from the right
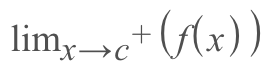
2.) The limit of the function approaching from the left exists
- Graphically, this would look like following a function to a certain point on the x-axis from the left
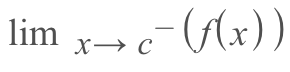
3.) The limit from the right equals the limit from the left
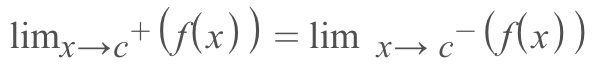
Study Guide: Determining Limits using the Squeeze Theorem
When doesn't a limit exist?
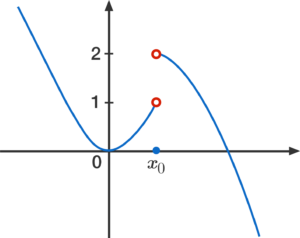
A limit MUST meet all three criteria in order for it to exist, which is important to remember especially when FRQ's come into play. If the limit from the left and the limit from the right are not equal, then the limit does not exist. An example of this would look something like this graph:
Here we can see that as we follow the function from the right hand side, it's going towards y = 2. On the left hand side, we see that the function is approaching y = 1. Since 2 ≄ 1, the limit does not exist at x = 1.
Study Guide: Exploring Types of Discontinuities
Limits Approaching Infinity
👉 Watch AP Calculus teacher Suzanne Ferrell-Locke explain limits @ infinity.
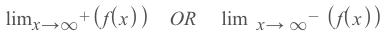
1.) Top-heavy
This is when the degree of the polynomial on the top of the function is greater than the degree of the polynomial in the denominator In this case, the answer you are finding is all dependent on whether or not you're being asked to be approaching negative or positive infinity. If you're approaching positive infinity, then the limit of a top-heavy function will also be infinity and vice versa.
2.) Middle-heavy
This is when the degrees of the numerator and denominator are the same. To find the limit here, you'll need to divide the leading coefficients of the numerator and denominator by each other.

For example, here we see that the degrees of the top and bottom are 3 and that the leading coefficient of the numerator is 5 and 2 for the denominator. Therefore, the limit of f(x) as x approaches positive infinity is 5/2.
3.) Bottom-heavy
This is when the degree of the denominator is greater than that of the numerator. If a function is bottom heavy, then the limit is zero, regardless if it is approaching positive or negative infinity
🎥Live Stream Replay: Continuity Part I
🎥Live Stream Replay: Continuity Part II
📌Here are some extra resources to help you out on limits approaching infinity!
- https://www.mathwarehouse.com/calculus/limits/what-is-a-limit.php
- https://unit8limits.weebly.com/infinite-limits.html
🎥Live Stream Replay: L'Hospital's Rule
What is a Limit?
3 min read•october 28, 2020
Rupi Adhikary
Rupi Adhikary
What is a limit?
A limit denotes the behavior of a function as it approaches a certain value which is especially important in calculus. In mathematical terms, the limit is asking the question "What value is 'y' getting close to as 'x' approaches a number?" and its represented by the expression:
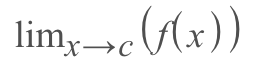
Out loud, this would sound something like "the limit of f(x) as x approaches c"
- The 'lim' shows that we're finding the limit and not the value of the function
- The 'x →c' tells us the value that x is getting closer and closer to but never actually reaching
- The 'f(x)' is meant to represent the functions you're working with
🎥Live Stream Replay: Algebraic Limits
Three Criteria for Limits to Exist
Study Guide: Determining Procedures for Determining Limits
1.) The limit of the function approaching from the right exists
- Graphically, this would look like following a function to a certain point on the x-axis from the right
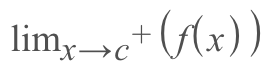
2.) The limit of the function approaching from the left exists
- Graphically, this would look like following a function to a certain point on the x-axis from the left
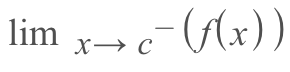
3.) The limit from the right equals the limit from the left
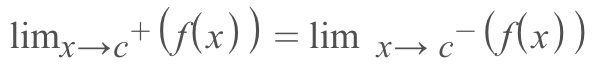
Study Guide: Determining Limits using the Squeeze Theorem
When doesn't a limit exist?
A limit MUST meet all three criteria in order for it to exist, which is important to remember especially when FRQ's come into play. If the limit from the left and the limit from the right are not equal, then the limit does not exist. An example of this would look something like this graph:
Here we can see that as we follow the function from the right hand side, it's going towards y = 2. On the left hand side, we see that the function is approaching y = 1. Since 2 ≄ 1, the limit does not exist at x = 1.

Study Guide: Exploring Types of Discontinuities
Limits Approaching Infinity
👉 Watch AP Calculus teacher Suzanne Ferrell-Locke explain limits @ infinity.
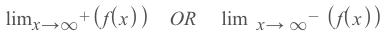
1.) Top-heavy
This is when the degree of the polynomial on the top of the function is greater than the degree of the polynomial in the denominator In this case, the answer you are finding is all dependent on whether or not you're being asked to be approaching negative or positive infinity. If you're approaching positive infinity, then the limit of a top-heavy function will also be infinity and vice versa.
2.) Middle-heavy
This is when the degrees of the numerator and denominator are the same. To find the limit here, you'll need to divide the leading coefficients of the numerator and denominator by each other.

For example, here we see that the degrees of the top and bottom are 3 and that the leading coefficient of the numerator is 5 and 2 for the denominator. Therefore, the limit of f(x) as x approaches positive infinity is 5/2.
3.) Bottom-heavy
This is when the degree of the denominator is greater than that of the numerator. If a function is bottom heavy, then the limit is zero, regardless if it is approaching positive or negative infinity
🎥Live Stream Replay: Continuity Part I
🎥Live Stream Replay: Continuity Part II
📌Here are some extra resources to help you out on limits approaching infinity!
- https://www.mathwarehouse.com/calculus/limits/what-is-a-limit.php
- https://unit8limits.weebly.com/infinite-limits.html
🎥Live Stream Replay: L'Hospital's Rule

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.