
Unit 7 Overview: Differential Equations
5 min read•february 15, 2024
Jacob Jeffries
Kashvi Panjolia
Jacob Jeffries
Kashvi Panjolia
Exam Weighting
Unit 7 makes up 6-12% of the AP Calculus AB exam and 6-9% of the AP Calculus BC exam. Euler's method and logistic differential equations/logistic growth are BC-only topics.
About Differential Equations
Differential equations are at the heart of mathematical modeling for all the sciences: physical, social, financial, et cetera.
Mathematical modeling is the use of math to describe physical situations. Essentially, math functions as a language. While some sciences prefer to put emphasis on traditional language to describe phenomena (we use words to describe explain biological happenings, for example) other sciences, like physics, rely on mathematical modeling to express ideas and concepts.
Mathematical modeling is useful because it often yields logical derivations that could not have been predicted in the first place. For example, the mathematical modeling of the behavior of particles directly led to the conclusion that subatomic particles can travel through a barrier of infinite energy, a deduction that would seem impossible through a different lens*.
Mathematical modeling also helps scientists confirm logical conclusions. Predictable actions like the behavior of a swinging pendulum with significant air friction** or the diffusion of diseases*** are supported and confirmed by mathematical modeling.
Differential equations serve as scaffolding for mathematical modeling because they relate something’s rate of change to itself. For example, the most popular model for long-term population-change is a logistic differential equation****:
.png?alt=media&token=847bb126-9e62-4d5a-ae87-934e4439c932)
In this case, P is the population (a function of time, t), L is the carrying capacity, and k is a constant.
Expressed literally, Eq. 1 says that this function is proportional to its first derivative and that (L-P) is proportional to its first derivative. This specific model will be discussed in more detail in section 7.6.
Differential equations are also very handy in finance. Specifically, differential equations are used for examining stock investments. The value of a stock will change over time relative to how many people are willing to invest in the stock, which is also a function of the price of the stock. The changing relationship of a stock’s rate of change to itself screams “differential equation,” as the stock’s value changes over time in relation to the original price of the stock.
Slope Fields
A slope field, also known as a direction field, is a graphical representation of a differential equation in the form dy/dx = f(x,y). It is a visual tool that can help you understand the behavior of the solution to the differential equation.
To create a slope field, you start by drawing a grid of evenly spaced horizontal and vertical lines on a graph. Then, at each point on the grid, you draw a small line segment with a slope that is determined by the value of f(x,y) at that point. The slope of the line segment at each point indicates the direction in which the solution to the differential equation is heading at that point. If f(x,y) evaluated to -4, the slope of the line segment at (x,y) would be negative and fairly steep. You do not have to be exact with slope fields, but you should be relatively correct. That is, the line segment for -4 should be steeper than the line segment for -1.
For example, if the value of f(x,y) is positive at a point, the slope of the line segment at that point will be positive, indicating that the solution is increasing at that point. If the value of f(x,y) is negative at a point, the slope of the line segment at that point will be negative, indicating that the solution is decreasing at that point.
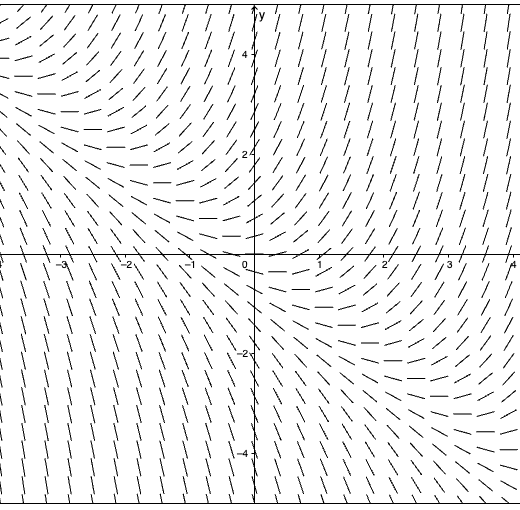
Image courtesy of GeoGebra.
This is an example of a slope field for the differential equation dy/dx = x + y. A slope field shows the different possible solutions for a general solution of a differential equation by translating the equation up and down the graph. At (0,1), dy/dx equals 1 because 0+1=1 when the x and y values are substituted into the right side of the differential equation. This means the slope of the line segment at (0,1) on the slope field is positive 1.
Euler's Method (BC only)
Euler's method is a formula for approximating the solution to a differential equation with a given initial value. It can be used to approximate the solution at discrete time intervals, starting from the initial value and working forward in time.
The basic idea behind Euler's method is to approximate the derivative dy/dx at a given point by using the slope of the tangent line to the solution curve at that point. The slope of the tangent line is given by the value of f(x,y), which is known.
To use Euler's method, you start by choosing a small step size h and a starting point (x0, y0). Then, you keep using the formula by substituting the values obtained in the previous iteration of the formula as your new x and y values to approximate the solution at each subsequent point using the formula:
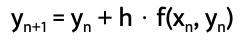
Practice Problems
.png?alt=media&token=75313da3-d109-487c-8dcf-0321b1bdebe0)
.png?alt=media&token=77d0c6c7-489b-488c-9989-efe39f4209be)
.png?alt=media&token=5f9a06ad-6792-4684-b136-9d4d32f7901b)
.png?alt=media&token=4d649f74-bf25-4a2f-b6be-a16f250c55d5)
.png?alt=media&token=369f5811-187f-4bc7-bc08-e4cfd068a29d)
.png?alt=media&token=54e54e75-285e-4ecd-9782-4e7fe23242f6)
.png?alt=media&token=68b382b1-b708-48e4-a003-7f0f7aedf659)
.png?alt=media&token=52993d29-19e0-4f04-a728-42d6ef536e7e)
.png?alt=media&token=a69886e4-0bb5-4947-8a8e-b629bdd29c86)
.png?alt=media&token=5518847f-3a34-46b1-b32f-367ab3f91019)
.png?alt=media&token=5f4ba147-0d59-4197-9335-d4f9e04e4cc9)
.png?alt=media&token=93512e09-d55d-49a6-975f-454c4025fb9d)
.png?alt=media&token=fce75257-5ea8-44e8-8b7f-d90290c50712)
.png?alt=media&token=3db7e321-4e07-4d66-bd54-4c4394c72daa)
.png?alt=media&token=7f4fe5eb-0daa-4bce-ab72-37a5aa90e62e)
Answers
B
A
D
D
B
C
A
C
A
A
A
C
B
B
C
Footnotes
*This is true because the differential equation that describes the probability density of a particle’s position under a delta function potential gives non-zero probability solutions for a particle tunneling through an infinite-potential barrier (if confined to a single axis):
.png?alt=media&token=ef1eb593-568b-41a5-8f86-b047d0f1f519)
**We logically expect the position of a swinging pendulum to look like a cosine graph that decreases in height with time. This matches the solution under a certain set of parameters:
.png?alt=media&token=add54270-6412-4ba3-a01f-83c69aa250c7)
***The diffusion of diseases in humans is complicated because medical research and other social factors are variables that are computationally difficult to account for. However, for more vulnerable species, such as bananas, one would expect the area of effect of the disease to exponentially increase with time, which approximately matches statistical data.
****This differential equation is often more useful than the exponential differential equation because it accounts for population capacity. Notice that for P << L, the differential equation has exponential solutions.
Key Terms to Review (13)
Carrying Capacity
: Carrying capacity refers to the maximum number of individuals that an environment can sustainably support without causing long-term damage or depletion of resources.Direction Field
: Direction fields are graphical representations used to visualize the behavior and solutions of first-order ordinary differential equations. They indicate the direction in which solutions tend to move at different points on a plane.dy/dx = f(x,y)
: This notation represents a general form of a first-order ordinary differential equation, where y is dependent on x and its derivative dy/dx is equal to some function f(x,y). It describes the relationship between the rate of change of y with respect to x.Euler's Method
: Euler's Method is a numerical approximation technique used to estimate the value of a function at certain points when its derivative is known. It involves using small steps and linear approximations based on the slope at each point.First Derivative
: The first derivative represents the rate at which a function is changing at any given point. It measures the slope of the tangent line to the graph of a function at that point.Initial Value
: The initial value, also known as the starting value or y-intercept, refers to the value of a function when the independent variable (usually denoted as x) is equal to zero.Logistic Differential Equations
: Logistic differential equations are a type of differential equation that models population growth or decay with a limiting factor. It takes into account both the rate of change and the carrying capacity of the population.Logistic Growth
: Logistic growth refers to a type of population growth that starts with exponential growth but eventually levels off due to limited resources or other factors.Population Change
: Population change refers to the increase or decrease in the number of individuals within a population over a specific period of time.Slope Fields
: Slope fields are graphical representations of differential equations that show the slope at various points on a plane. They help visualize the behavior and solutions of differential equations.Step Size h
: Step size h refers to the width between two consecutive points on an interval when approximating values using numerical methods such as Euler's method or Riemann sums. It determines how accurate and precise our approximation will be.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.Unit 7
: Unit 7 refers to a specific section of the AP Calculus AB/BC curriculum that covers techniques and applications of integration. It includes topics such as integration by parts, trigonometric integrals, partial fractions, and applications of definite integrals.Unit 7 Overview: Differential Equations
5 min read•february 15, 2024
Jacob Jeffries
Kashvi Panjolia
Jacob Jeffries
Kashvi Panjolia
Exam Weighting
Unit 7 makes up 6-12% of the AP Calculus AB exam and 6-9% of the AP Calculus BC exam. Euler's method and logistic differential equations/logistic growth are BC-only topics.
About Differential Equations
Differential equations are at the heart of mathematical modeling for all the sciences: physical, social, financial, et cetera.
Mathematical modeling is the use of math to describe physical situations. Essentially, math functions as a language. While some sciences prefer to put emphasis on traditional language to describe phenomena (we use words to describe explain biological happenings, for example) other sciences, like physics, rely on mathematical modeling to express ideas and concepts.
Mathematical modeling is useful because it often yields logical derivations that could not have been predicted in the first place. For example, the mathematical modeling of the behavior of particles directly led to the conclusion that subatomic particles can travel through a barrier of infinite energy, a deduction that would seem impossible through a different lens*.
Mathematical modeling also helps scientists confirm logical conclusions. Predictable actions like the behavior of a swinging pendulum with significant air friction** or the diffusion of diseases*** are supported and confirmed by mathematical modeling.
Differential equations serve as scaffolding for mathematical modeling because they relate something’s rate of change to itself. For example, the most popular model for long-term population-change is a logistic differential equation****:
.png?alt=media&token=847bb126-9e62-4d5a-ae87-934e4439c932)
In this case, P is the population (a function of time, t), L is the carrying capacity, and k is a constant.
Expressed literally, Eq. 1 says that this function is proportional to its first derivative and that (L-P) is proportional to its first derivative. This specific model will be discussed in more detail in section 7.6.
Differential equations are also very handy in finance. Specifically, differential equations are used for examining stock investments. The value of a stock will change over time relative to how many people are willing to invest in the stock, which is also a function of the price of the stock. The changing relationship of a stock’s rate of change to itself screams “differential equation,” as the stock’s value changes over time in relation to the original price of the stock.
Slope Fields
A slope field, also known as a direction field, is a graphical representation of a differential equation in the form dy/dx = f(x,y). It is a visual tool that can help you understand the behavior of the solution to the differential equation.
To create a slope field, you start by drawing a grid of evenly spaced horizontal and vertical lines on a graph. Then, at each point on the grid, you draw a small line segment with a slope that is determined by the value of f(x,y) at that point. The slope of the line segment at each point indicates the direction in which the solution to the differential equation is heading at that point. If f(x,y) evaluated to -4, the slope of the line segment at (x,y) would be negative and fairly steep. You do not have to be exact with slope fields, but you should be relatively correct. That is, the line segment for -4 should be steeper than the line segment for -1.
For example, if the value of f(x,y) is positive at a point, the slope of the line segment at that point will be positive, indicating that the solution is increasing at that point. If the value of f(x,y) is negative at a point, the slope of the line segment at that point will be negative, indicating that the solution is decreasing at that point.

Image courtesy of GeoGebra.
This is an example of a slope field for the differential equation dy/dx = x + y. A slope field shows the different possible solutions for a general solution of a differential equation by translating the equation up and down the graph. At (0,1), dy/dx equals 1 because 0+1=1 when the x and y values are substituted into the right side of the differential equation. This means the slope of the line segment at (0,1) on the slope field is positive 1.
Euler's Method (BC only)
Euler's method is a formula for approximating the solution to a differential equation with a given initial value. It can be used to approximate the solution at discrete time intervals, starting from the initial value and working forward in time.
The basic idea behind Euler's method is to approximate the derivative dy/dx at a given point by using the slope of the tangent line to the solution curve at that point. The slope of the tangent line is given by the value of f(x,y), which is known.
To use Euler's method, you start by choosing a small step size h and a starting point (x0, y0). Then, you keep using the formula by substituting the values obtained in the previous iteration of the formula as your new x and y values to approximate the solution at each subsequent point using the formula:
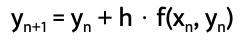
Practice Problems
.png?alt=media&token=75313da3-d109-487c-8dcf-0321b1bdebe0)
.png?alt=media&token=77d0c6c7-489b-488c-9989-efe39f4209be)
.png?alt=media&token=5f9a06ad-6792-4684-b136-9d4d32f7901b)
.png?alt=media&token=4d649f74-bf25-4a2f-b6be-a16f250c55d5)
.png?alt=media&token=369f5811-187f-4bc7-bc08-e4cfd068a29d)
.png?alt=media&token=54e54e75-285e-4ecd-9782-4e7fe23242f6)
.png?alt=media&token=68b382b1-b708-48e4-a003-7f0f7aedf659)
.png?alt=media&token=52993d29-19e0-4f04-a728-42d6ef536e7e)
.png?alt=media&token=a69886e4-0bb5-4947-8a8e-b629bdd29c86)
.png?alt=media&token=5518847f-3a34-46b1-b32f-367ab3f91019)
.png?alt=media&token=5f4ba147-0d59-4197-9335-d4f9e04e4cc9)
.png?alt=media&token=93512e09-d55d-49a6-975f-454c4025fb9d)
.png?alt=media&token=fce75257-5ea8-44e8-8b7f-d90290c50712)
.png?alt=media&token=3db7e321-4e07-4d66-bd54-4c4394c72daa)
.png?alt=media&token=7f4fe5eb-0daa-4bce-ab72-37a5aa90e62e)
Answers
B
A
D
D
B
C
A
C
A
A
A
C
B
B
C
Footnotes
*This is true because the differential equation that describes the probability density of a particle’s position under a delta function potential gives non-zero probability solutions for a particle tunneling through an infinite-potential barrier (if confined to a single axis):
.png?alt=media&token=ef1eb593-568b-41a5-8f86-b047d0f1f519)
**We logically expect the position of a swinging pendulum to look like a cosine graph that decreases in height with time. This matches the solution under a certain set of parameters:
.png?alt=media&token=add54270-6412-4ba3-a01f-83c69aa250c7)
***The diffusion of diseases in humans is complicated because medical research and other social factors are variables that are computationally difficult to account for. However, for more vulnerable species, such as bananas, one would expect the area of effect of the disease to exponentially increase with time, which approximately matches statistical data.
****This differential equation is often more useful than the exponential differential equation because it accounts for population capacity. Notice that for P << L, the differential equation has exponential solutions.
Key Terms to Review (13)
Carrying Capacity
: Carrying capacity refers to the maximum number of individuals that an environment can sustainably support without causing long-term damage or depletion of resources.Direction Field
: Direction fields are graphical representations used to visualize the behavior and solutions of first-order ordinary differential equations. They indicate the direction in which solutions tend to move at different points on a plane.dy/dx = f(x,y)
: This notation represents a general form of a first-order ordinary differential equation, where y is dependent on x and its derivative dy/dx is equal to some function f(x,y). It describes the relationship between the rate of change of y with respect to x.Euler's Method
: Euler's Method is a numerical approximation technique used to estimate the value of a function at certain points when its derivative is known. It involves using small steps and linear approximations based on the slope at each point.First Derivative
: The first derivative represents the rate at which a function is changing at any given point. It measures the slope of the tangent line to the graph of a function at that point.Initial Value
: The initial value, also known as the starting value or y-intercept, refers to the value of a function when the independent variable (usually denoted as x) is equal to zero.Logistic Differential Equations
: Logistic differential equations are a type of differential equation that models population growth or decay with a limiting factor. It takes into account both the rate of change and the carrying capacity of the population.Logistic Growth
: Logistic growth refers to a type of population growth that starts with exponential growth but eventually levels off due to limited resources or other factors.Population Change
: Population change refers to the increase or decrease in the number of individuals within a population over a specific period of time.Slope Fields
: Slope fields are graphical representations of differential equations that show the slope at various points on a plane. They help visualize the behavior and solutions of differential equations.Step Size h
: Step size h refers to the width between two consecutive points on an interval when approximating values using numerical methods such as Euler's method or Riemann sums. It determines how accurate and precise our approximation will be.Tangent Line
: A tangent line is a straight line that touches a curve at only one point without crossing through it. In calculus, we use tangent lines to approximate curves and find instantaneous rates of change.Unit 7
: Unit 7 refers to a specific section of the AP Calculus AB/BC curriculum that covers techniques and applications of integration. It includes topics such as integration by parts, trigonometric integrals, partial fractions, and applications of definite integrals.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.