
Unit 1 Review - Limits & Continuity
7 min read•october 28, 2020
Rachel Ikhilov
Rachel Ikhilov
AP Calculus Basics
We all know that iconic scene from Mean Girls. The one where Cady competes in the Mathletics competition and puts Marymount High to shame as she utters this famous line:

However, what exactly is a limit? How can we solve them? Here is an organized outline based on the 2019 College Board Course Description. You can use to form a study guide for your next AP Calc test, the actual AP exam, and (of course) to beat the Northshore High mathletes!
🤓 There's more AP Calculus review inside of Fiveable. Check out all the guides, slides, and videos!
Introducing Calculus: Can Change Occur at an Instant?
In AP Calculus, limits can be used to represent constant change in functions.
The rate of change of a function is equal to...
Δy/Δx or (y2-y1)/(x2-x1)
Because of this, if the x value does not change, the average rate of change would be undefined.
Defining Limits Using Limit Notation
⚡️Watch - AP Calculus AB/BC: Graphical Limits
A limit, is the y value a function approaches as it approaches a certain x value.
On the AP Exam, they will be written in this notation:

This means that as x approaches a, on the graph of f(x), the value on the y-axis that the function approaches is L
Limits can be solved for on a graph- follow the function to as close to the x value it approaches as possible and then look at what value you have reached
Also, limits can also be solved for by plugging in the x value: Plug the x value into the function and if you get 0/0 or indeterminate, then solve for it algebraically. If you get an actual number, then that's your answer!
Limits can be solved algebraically - simplify the function as much as possible, and when you are done, plug in the x value and you will get your answer!
Estimating Limit Values from Graphs
Limits that have a positive or negative sign at the top of the x value it is approaching are called single-handed limits. If it has a positive sign, you only follow the function from your right-hand side and see what y value it approaches as it approaches a certain x value from the right side. The function to the left should not influence your answer at all. With the left, vice versa.
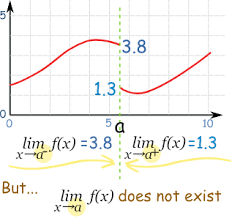
If there is no sign on top, that means that it is a double-handed limit and you have to find the limit of both the right and the left-hand limit.
If they are the same, that is your answer. Also, if they're different, like the example above, then "the limit does not exist!"
In addition, if a single or double-handed limit is going to either positive or negative infinity, then the limit does not exist either.
Estimating Limit Values from Tables and Determining Limits Using Algebraic Properties of Limits
⚡️Watch - AP Calculus AB/BC: Algebraic Limits
You can also find the limit as a function approaches a certain number through a table.

Since as x approaches 3, the y value is approaching 0.25, it is clear that as x approaches 3, the limit of the function on the table is 0.25.
This can also be used to find single-handed limits. For a left-handed limit, go from x values from negative infinity to 3 and for the right hand, look at the y values that correspond to the y values coming from 3 to positive infinity.
Determining Limits Using Algebraic Manipulation and Selecting Procedures for Determining Limits
There are multiple ways we can solve for limits. Not only can you find them on a graph or table, but you can find them algebraically!
When you have a double-handed limit to solve for, first try and plug in the value it is approaching as x. If you get a number, that's your limit.
If you get 0/0, that means that you need to simplify the function before plugging in the x-value. Simplify it as much as possible. Then plug in the x value the limit approaches as x and that is your answer.
Determining Limits Using the Squeeze Theorem
⚡ Read- AP Calculus AB/BC: Squeeze Theorem
Another way to solve for a limit is using the Squeeze Theorem.
If the limit of a certain function is too hard to solve for, you can solve for the limit of similar, easier functions to help you.
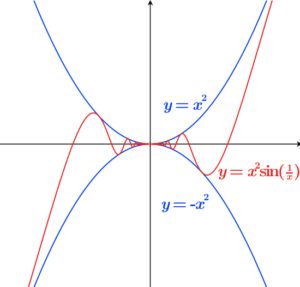
As you can see here, while the limit of the function in the red may be hard to solve for, the similar functions in the blue helps us figure out that the limit of the function will still be zero.
Exploring Types of Discontinuities
⚡️Watch- AP Calculus AB/BC: Continuity, Part II
Generally speaking, a discontinuity is a break in physical continuity or sequence in time. So, if applied here it is a break in the continuity of a function. In this course, you will need to know that functions have 3 types of discontinuities.
Jump discontinuity: If the left and right-handed limits aren't equal, then the double-handed limit does not exist. In this scenario, we would have a jump discontinuity. (DNE). The graph of that would look something like this:
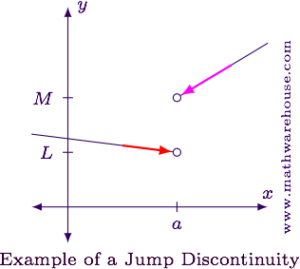
As you can see, there is a break in the physical continuity of the graph at x. If the limit from both sides is different, how can we find a specific value that the function approaches? We cant. Therefore, the limit DNE.
Infinite discontinuity: Also, if f(x) isn't approaching a specific y value and is approaching + or -, the limit does not exist. (DNE). In this scenario, we would have an infinite discontinuity. The graph would look something like this:

As you can see, as the graph gets closer and closer to x, the y-value just keeps increasing exponentially. It’s not approaching any kind of specific y value, it’s going to infinity. And therefore, the limit DNE.
Removable discontinuity: Finally, if f(x) is continuous with a hole at a, then the limit as x approaches a does exist, but you can’t just look at f(a) to find it. In this scenario, we would have a removable discontinuity. The graph would look something like this:
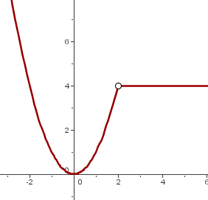
Defining Continuity at a Point of Interval
⚡️Watch- AP Calculus AB/BC: Continuity, Part I
As you can see, the double-sided limit here does exist because the function approaches the same value from both sides at x. But just looking at the graph at f(x) will not give you the answer because there is a discontinuity there.
We know a function is continuous at a certain point if the function continues and crosses that point without any break or interruption.
For instance, the function above is continuous at x=1 but not x=2.
If a function is defined only for a certain interval. (For instance: f(x)=x^2 for [1,5]), then the function will be continuous on that interval.
This works for functions like polynomial, logarithmic, and exponential.
Removing Discontinuities
On your exam, you may come across a piecewise function. These are very interesting because sometimes they can be continuous, but at other times, they cant be.
A piecewise function cant be continuous if the values of the functions on both sides of a boundary (defined by the piecewise function) are not equal.
If they are equal, then it would be continuous. For example, although the function below is piecewise, it is continuous.
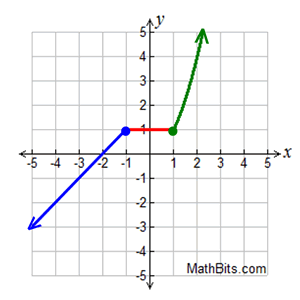
Connecting Infinite Limits and Vertical Asymptotes or Horizontal Asymptotes
An asymptote is a line that approaches a given curve but does not meet it at any distance. By now, we have already covered one of the asymptotes you need to know for this course. (Infinite discontinuities). This is a vertical asymptote. The value x is approaching is the asymptote because the function goes closer and closer to that x value. Meanwhile, the y value continues to increase. In other words, you have a vertical asymptote if
lim x→a- f(x)=±∞ or lim x→a+ f(x)= ±∞
...and if that is the case, them x= a is your vertical asymptote.
However, there is another type of asymptote (Horizontal asymptote)
If limx→a=±∞f(x)=k, and k=ℝ, then y=k is a horizontal asymptote.
As the x value continues to increase and goes to infinity, the function will be getting closer and closer to k, but it won't cross it. Therefore, y=k would have to be the horizontal asymptote.
Working with the Intermediate Value Theorem
⚡ Read- AP Calculus AB/BC: The Intermediate Value Theorem
If a function is continuous on a certain domain or interval, and a certain value (c) is a y value corresponding to a x value in the domain, then it has to hit that y value at least once in that interval.
If f is continuous on the closed interval [a,b], and k is any number between f(a) and f(b), then there is at least one number c in [a,b] such that f(c) = k. (Taken from Larson Hostetler Edwrds calculus eighth edition textbook)
I hope this article was useful to you. Best of luck on your exam! 😁
Unit 1 Review - Limits & Continuity
7 min read•october 28, 2020
Rachel Ikhilov
Rachel Ikhilov
AP Calculus Basics
We all know that iconic scene from Mean Girls. The one where Cady competes in the Mathletics competition and puts Marymount High to shame as she utters this famous line:

However, what exactly is a limit? How can we solve them? Here is an organized outline based on the 2019 College Board Course Description. You can use to form a study guide for your next AP Calc test, the actual AP exam, and (of course) to beat the Northshore High mathletes!
🤓 There's more AP Calculus review inside of Fiveable. Check out all the guides, slides, and videos!
Introducing Calculus: Can Change Occur at an Instant?
In AP Calculus, limits can be used to represent constant change in functions.
The rate of change of a function is equal to...
Δy/Δx or (y2-y1)/(x2-x1)
Because of this, if the x value does not change, the average rate of change would be undefined.
Defining Limits Using Limit Notation
⚡️Watch - AP Calculus AB/BC: Graphical Limits
A limit, is the y value a function approaches as it approaches a certain x value.
On the AP Exam, they will be written in this notation:

This means that as x approaches a, on the graph of f(x), the value on the y-axis that the function approaches is L
Limits can be solved for on a graph- follow the function to as close to the x value it approaches as possible and then look at what value you have reached
Also, limits can also be solved for by plugging in the x value: Plug the x value into the function and if you get 0/0 or indeterminate, then solve for it algebraically. If you get an actual number, then that's your answer!
Limits can be solved algebraically - simplify the function as much as possible, and when you are done, plug in the x value and you will get your answer!
Estimating Limit Values from Graphs
Limits that have a positive or negative sign at the top of the x value it is approaching are called single-handed limits. If it has a positive sign, you only follow the function from your right-hand side and see what y value it approaches as it approaches a certain x value from the right side. The function to the left should not influence your answer at all. With the left, vice versa.

If there is no sign on top, that means that it is a double-handed limit and you have to find the limit of both the right and the left-hand limit.
If they are the same, that is your answer. Also, if they're different, like the example above, then "the limit does not exist!"
In addition, if a single or double-handed limit is going to either positive or negative infinity, then the limit does not exist either.
Estimating Limit Values from Tables and Determining Limits Using Algebraic Properties of Limits
⚡️Watch - AP Calculus AB/BC: Algebraic Limits
You can also find the limit as a function approaches a certain number through a table.

Since as x approaches 3, the y value is approaching 0.25, it is clear that as x approaches 3, the limit of the function on the table is 0.25.
This can also be used to find single-handed limits. For a left-handed limit, go from x values from negative infinity to 3 and for the right hand, look at the y values that correspond to the y values coming from 3 to positive infinity.
Determining Limits Using Algebraic Manipulation and Selecting Procedures for Determining Limits
There are multiple ways we can solve for limits. Not only can you find them on a graph or table, but you can find them algebraically!
When you have a double-handed limit to solve for, first try and plug in the value it is approaching as x. If you get a number, that's your limit.
If you get 0/0, that means that you need to simplify the function before plugging in the x-value. Simplify it as much as possible. Then plug in the x value the limit approaches as x and that is your answer.
Determining Limits Using the Squeeze Theorem
⚡ Read- AP Calculus AB/BC: Squeeze Theorem
Another way to solve for a limit is using the Squeeze Theorem.
If the limit of a certain function is too hard to solve for, you can solve for the limit of similar, easier functions to help you.

As you can see here, while the limit of the function in the red may be hard to solve for, the similar functions in the blue helps us figure out that the limit of the function will still be zero.
Exploring Types of Discontinuities
⚡️Watch- AP Calculus AB/BC: Continuity, Part II
Generally speaking, a discontinuity is a break in physical continuity or sequence in time. So, if applied here it is a break in the continuity of a function. In this course, you will need to know that functions have 3 types of discontinuities.
Jump discontinuity: If the left and right-handed limits aren't equal, then the double-handed limit does not exist. In this scenario, we would have a jump discontinuity. (DNE). The graph of that would look something like this:

As you can see, there is a break in the physical continuity of the graph at x. If the limit from both sides is different, how can we find a specific value that the function approaches? We cant. Therefore, the limit DNE.
Infinite discontinuity: Also, if f(x) isn't approaching a specific y value and is approaching + or -, the limit does not exist. (DNE). In this scenario, we would have an infinite discontinuity. The graph would look something like this:

As you can see, as the graph gets closer and closer to x, the y-value just keeps increasing exponentially. It’s not approaching any kind of specific y value, it’s going to infinity. And therefore, the limit DNE.
Removable discontinuity: Finally, if f(x) is continuous with a hole at a, then the limit as x approaches a does exist, but you can’t just look at f(a) to find it. In this scenario, we would have a removable discontinuity. The graph would look something like this:

Defining Continuity at a Point of Interval
⚡️Watch- AP Calculus AB/BC: Continuity, Part I
As you can see, the double-sided limit here does exist because the function approaches the same value from both sides at x. But just looking at the graph at f(x) will not give you the answer because there is a discontinuity there.
We know a function is continuous at a certain point if the function continues and crosses that point without any break or interruption.
For instance, the function above is continuous at x=1 but not x=2.
If a function is defined only for a certain interval. (For instance: f(x)=x^2 for [1,5]), then the function will be continuous on that interval.
This works for functions like polynomial, logarithmic, and exponential.
Removing Discontinuities
On your exam, you may come across a piecewise function. These are very interesting because sometimes they can be continuous, but at other times, they cant be.
A piecewise function cant be continuous if the values of the functions on both sides of a boundary (defined by the piecewise function) are not equal.
If they are equal, then it would be continuous. For example, although the function below is piecewise, it is continuous.

Connecting Infinite Limits and Vertical Asymptotes or Horizontal Asymptotes
An asymptote is a line that approaches a given curve but does not meet it at any distance. By now, we have already covered one of the asymptotes you need to know for this course. (Infinite discontinuities). This is a vertical asymptote. The value x is approaching is the asymptote because the function goes closer and closer to that x value. Meanwhile, the y value continues to increase. In other words, you have a vertical asymptote if
lim x→a- f(x)=±∞ or lim x→a+ f(x)= ±∞
...and if that is the case, them x= a is your vertical asymptote.
However, there is another type of asymptote (Horizontal asymptote)
If limx→a=±∞f(x)=k, and k=ℝ, then y=k is a horizontal asymptote.
As the x value continues to increase and goes to infinity, the function will be getting closer and closer to k, but it won't cross it. Therefore, y=k would have to be the horizontal asymptote.
Working with the Intermediate Value Theorem
⚡ Read- AP Calculus AB/BC: The Intermediate Value Theorem
If a function is continuous on a certain domain or interval, and a certain value (c) is a y value corresponding to a x value in the domain, then it has to hit that y value at least once in that interval.
If f is continuous on the closed interval [a,b], and k is any number between f(a) and f(b), then there is at least one number c in [a,b] such that f(c) = k. (Taken from Larson Hostetler Edwrds calculus eighth edition textbook)
I hope this article was useful to you. Best of luck on your exam! 😁

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.