Constrained optimization problems are all about finding the best solution while playing by the rules. We're trying to maximize or minimize something important, like profit or efficiency, but we can't just do whatever we want. We have to follow certain restrictions.
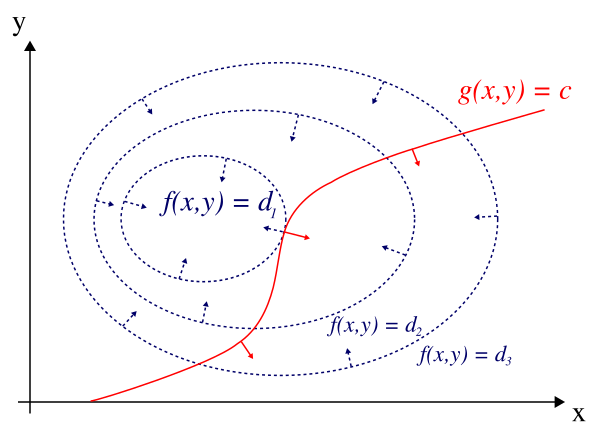
These problems have three key parts: the objective function (what we're trying to optimize), constraints (the rules we have to follow), and the feasible region (where we're allowed to look for solutions). It's like a puzzle where we need to find the best answer within specific boundaries.
Optimization Problem Components
Constrained Optimization Fundamentals
- Constrained optimization involves finding the optimal solution to a problem while satisfying certain restrictions or limitations
- An objective function represents the quantity or goal to be maximized or minimized in the optimization problem (profit, cost, efficiency)
- A constraint equation defines the limitations or restrictions that must be satisfied while optimizing the objective function (budget, resources, physical limitations)
- The feasible region consists of all possible solutions that satisfy the given constraints in the optimization problem
Constraint Classifications
- Equality constraints require the solution to exactly meet a specific condition or value ($x + y = 10$)
- Inequality constraints allow the solution to be less than or greater than a specific value or within a certain range ($x \leq 5$, $y \geq 3$)

Constraint Types
Binding and Non-Binding Constraints
- Binding constraints are active constraints that directly impact the optimal solution by limiting the feasible region (budget constraint in a production optimization problem)
- Non-binding constraints are inactive constraints that do not affect the optimal solution as they are not restricting the feasible region (a constraint that is automatically satisfied by the optimal solution)
Identifying Constraint Types
- Determine if a constraint is binding by checking if the optimal solution lies on the boundary of the constraint
- Non-binding constraints can be identified when the optimal solution is not limited by the constraint and lies within the feasible region
Optimal Solutions
Local and Global Extrema
- Local extrema are the optimal solutions within a specific neighborhood or region of the feasible set (a local maximum or minimum point)
- Global extrema are the overall best solutions in the entire feasible region, considering all possible local extrema (the absolute maximum or minimum point)
Finding Optimal Solutions
- Identify the objective function and constraints of the optimization problem
- Determine the feasible region by graphing the constraints or using analytical methods
- Locate the local extrema by finding the points where the objective function reaches a maximum or minimum value within the feasible region (using derivatives, critical points, or graphical methods)
- Compare the local extrema to identify the global extrema, which yields the optimal solution to the problem (by evaluating the objective function at each local extremum)