8.2 The method of Lagrange multipliers

Lagrange multipliers are a powerful tool for solving constrained optimization problems. They allow us to find the maximum or minimum values of a function subject to specific constraints, turning complex problems into simpler ones.

This method introduces a new variable, λ, which helps balance the objective function and constraints. By using Lagrange multipliers, we can tackle real-world problems like maximizing profits or minimizing costs while working within given limitations.

Lagrange Multipliers and Lagrangian Function

Lagrange Multiplier and Lagrangian Function

Top images from around the web for Lagrange Multiplier and Lagrangian Function

• 

  Lagrange Multipliers · Calculus View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

• 

  Lagrange Multipliers · Calculus View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

1 of 3

Top images from around the web for Lagrange Multiplier and Lagrangian Function

• 

  Lagrange Multipliers · Calculus View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

• 

  Lagrange Multipliers · Calculus View original

  Is this image relevant?

• 

  Lagrange multiplier - Wikipedia View original

  Is this image relevant?

1 of 3

• Lagrange multiplier ($\lambda$) introduced to solve constrained optimization problems
• Converts a constrained optimization problem into an unconstrained one by incorporating the constraints into the objective function
• Lagrangian function ($L$) formed by combining the objective function $f(x, y)$ and the constraint function $g(x, y)$ using Lagrange multipliers
  • $L(x, y, \lambda) = f(x, y) + \lambda g(x, y)$
  • Example: Minimize $f(x, y) = x^2 + y^2$ subject to $g(x, y) = x + y - 1 = 0$
    • Lagrangian function: $L(x, y, \lambda) = x^2 + y^2 + \lambda(x + y - 1)$

Critical Points and Lagrange Multiplier Theorem

• Critical points of the Lagrangian function found by setting the partial derivatives equal to zero
  • $\frac{\partial L}{\partial x} = 0$, $\frac{\partial L}{\partial y} = 0$, and $\frac{\partial L}{\partial \lambda} = 0$
  • Solving this system of equations yields the critical points $(x, y, \lambda)$
• Lagrange multiplier theorem states that if $(x_0, y_0)$ is a local extremum of $f(x, y)$ subject to the constraint $g(x, y) = 0$, then there exists a Lagrange multiplier $\lambda_0$ such that $(x_0, y_0, \lambda_0)$ is a critical point of the Lagrangian function
  • Provides a necessary condition for constrained optimization problems
  • Example: For the problem above, the critical points are $(0, 1, -2)$ and $(1, 0, -2)$

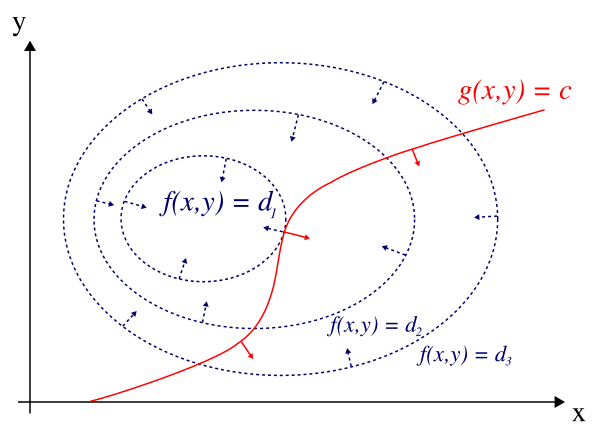
Gradient Vectors and Parallel Gradients

Gradient Vectors and Parallel Gradients

• Gradient vector $\nabla f(x, y)$ is a vector perpendicular to the level curve of $f(x, y)$ at a given point
  • $\nabla f(x, y) = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)$
• At the optimal solution, the gradient vectors of the objective function and the constraint function are parallel
  • $\nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0)$
  • Geometrically, this means that the level curves of $f(x, y)$ and $g(x, y)$ are tangent at the optimal point

First-Order Necessary and Second-Order Sufficient Conditions

• First-order necessary conditions for a point $(x_0, y_0)$ to be a local extremum of $f(x, y)$ subject to $g(x, y) = 0$
  1. $g(x_0, y_0) = 0$ (the point satisfies the constraint)
  2. $\nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0)$ for some $\lambda$ (gradient vectors are parallel)
• Second-order sufficient conditions help classify the critical points as local minima, local maxima, or saddle points
  • Involves examining the Hessian matrix of the Lagrangian function at the critical points
  • Example: For the problem above, $(0, 1, -2)$ is a local minimum, and $(1, 0, -2)$ is a local maximum

Constrained Optimization

Saddle Points and Multiple Constraints

• Saddle points are critical points that are neither local minima nor local maxima
  • Occur when the Hessian matrix of the Lagrangian function has both positive and negative eigenvalues
  • Represent points where the objective function increases in some directions and decreases in others
• Problems with multiple constraints can be solved using Lagrange multipliers by introducing a Lagrange multiplier for each constraint
  • Lagrangian function: $L(x, y, \lambda_1, \lambda_2, \ldots, \lambda_n) = f(x, y) + \lambda_1 g_1(x, y) + \lambda_2 g_2(x, y) + \ldots + \lambda_n g_n(x, y)$
  • First-order necessary conditions: $\nabla f(x_0, y_0) = \lambda_1 \nabla g_1(x_0, y_0) + \lambda_2 \nabla g_2(x_0, y_0) + \ldots + \lambda_n \nabla g_n(x_0, y_0)$
  • Example: Minimize $f(x, y) = x^2 + y^2$ subject to $g_1(x, y) = x + y - 1 = 0$ and $g_2(x, y) = x - y - 1 = 0$
    • Lagrangian function: $L(x, y, \lambda_1, \lambda_2) = x^2 + y^2 + \lambda_1(x + y - 1) + \lambda_2(x - y - 1)$