
AP Stats Practice FRQ Responses & Feedback (Unit 4)
14 min read•january 5, 2021
Jerry Kosoff
Jerry Kosoff
Practicing with FRQs is a great way to prep for the AP exam! Work through this prompt from Unit 3, then review student responses and corresponding feedback from Fiveable teacher Jerry Kosoff!
The Practice FRQ Prompt
A large group of voters in two nearby counties were surveyed about which political party they prefer between parties X, Y, and Z. The relative frequencies in the table below summarize the results of the survey.
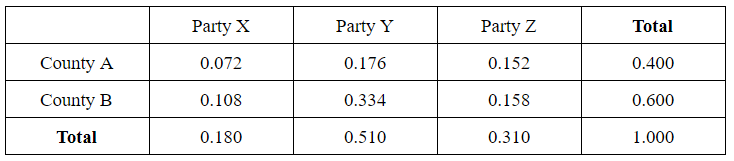
a. If one surveyed person is selected at random:
i. What is the probability that the person lives in County A and prefers Party Z
ii. What is the probability that the person lives in County A or prefers Party Z?
iii. What is the probability that the person lives in County A, given that they prefer Party Z?
b. In the survey, are the events “Lives in County B” and “Prefers Party X” independent? Explain why or why not.
c. Assume that the distribution of party preference shown in the table holds true in the entire state. If 5 voters from the state are selected at random, what is the probability that exactly 2 of them prefer Party Y?
FRQ Writing Samples and Teacher Feedback
Student Response 1
a) i. P(County A and Party Z) = 0.152. There is a 0.152 probability that the person lives in County A and prefers Party Z.
ii) P(County A or Party Z) = P(County A) + P(Party Z) - P(County A and Party Z)
P(County A or Party Z) = 0.4 + 0.31 - 0.152 = 0.558. There is a 0.558 probability that the person lives in County A or prefers Party Z.
iii) P(County A|Party Z) = P(County A and Party Z) / P(Party Z) = 0.152 / 0.31 = 0.49. There is a 0.49 probability that the person lives in County A, given that they prefer Party Z.
b) If independent, P(Lives in County B and Prefers Party X) = P(Lives in County B) * P(Prefers Party X).
0.108 = 0.6 * 0.18 = 0.108
The events “Lives in County B” and “Prefers Party X” are independent, as the two events satisfy the multiplication rule for independent events.
c) Binomial Distribution Conditions - Binary - Party Y or not Party Y, Independent - reasonable to assume preferences of 5 voters are independent from each other, Number of Trials = 5 voters are selected at random (n=5), S = probability of selecting a voter who prefers Party Y is the same for every voter selected (p = 0.51)
X = the number of voters who prefer Party Y when the distribution of X is binomial with p = 0.51 and n = 5
P(X=2) = 0.306 using binomialpdf with p = 0.51, n = 5, and successes = 2.
There is a 0.306 probability that exactly two voters prefer Party Y if 5 voters from the state are selected at random.
Teacher Feedback
Well done! All three parts show strong command of statistical notation, and clear communication. Your answers are all correct and would all earn credit.
Student Response 2
a.) i. P(County A AND Party Z)= 0.152. There is a 15.2% chance that the person lives in County A and prefers Party Z.
ii.) P(County A OR Party Z)=0.400+0.310-0.152=0.558. There is a 55.8% chance that the person lives in County A or prefers Party Z
iii.) P(County A|Party Z)=0.152/0.310=0.490. There is a 49% chance that the person lives in County A given that they prefer Party Z.
b.) P(County B)= 0.600, P(County B|Party X)=0.108/0.180=0.60. Because the two probabilities are the same, the events “Live in County B” and “Prefers Party X” are independent.
c.) This scenario has each trial ends is either a success or failure, they are independent, the 2 selected are set, and the probability for those who prefer Party Y is the same at 0.510. Therefore, this is a binomial probability.
P(X=2)= BinomPDF(n=5, p=0.510, x=2)=0.306
There is a 30.6% chance that if 5 voters from the state are selected at random, exactly 2 of them will prefer Party Y.
Teacher Feedback
In all three parts, your answers are correct and presented with accompanying work and appropriate notation. You would get full credit for each part! Part ( c ) provides a good contrast to your work on Unit 4 FRQ #2 - by saying “the probability for those who prefer Party Y is the same at 0.510,” you provide an in-context reason for the scenario being binomial. Well done!
Student Response 3
A i. P(County A and Party Z)=.152/1=.152
ii. P(County A or Party Z)= .400+.310-.152=.558
iii. P(County A/Party Z)= .152/.310=.490
B. Yes, “lives in county B” and “prefers party x” are independent because:
P(County B/Party X)= P(County B): P(.6)= P(.600)
P(Party X/County B)= P(Party X): P(.18)= P(.180)
C. The probability that exactly 2 of them prefer Party Y is .306.
To find out I first check the binomial distribution requirements:
- Each trial has 2 possible outcomes (Party Y or not party Y)
- There are fixed number of trials (n=5)
- Outcomes are independent
- Probability of success is the same for each trial (p=.510)
I then proceeded to put on my calculator binompdf( 5, .510, 2). I knew to use the function binompdf because the problem is asking to find exactly 2 voters.
Teacher Feedback
All calculations and explanations are correct, with appropriate work shown. However, in part (b), you make a small notation error. P(County B | Party X) = P(County B) = 0.6. The probabilities themselves should not be inside the P( ) notation. Think of it like input/output function notation - inside the P( ) is what probability you’re finding (in words or symbols), while outside on the other side of the equals sign is the numerical answer.
Student Response 4
a i) The probability that a person lives in Country A and prefers Party Z is 0.152.
ii) The probability that the person lives in County A or prefers Party Z is 0.558.
P(AUB) = P(person lives in county A) + P(Person prefers Party Z) - P(person who lives in Country A and prefers Party Z)= 0.558
iii) P(Person lives in County A | Person prefers Party Z) = 0.152/0.310= 0.490
b) P(Living in County B)= 0.600 P(Living in County B | Prefers Party X)=0.108/ 0.180= 0.6
The events “Lives in County B” and "Prefers Party X"are independent as the probability of Living in County B equals the probability of living in county B given preferring Party X.
c. Binomial Distribution conditions:
Binary: Prefer Party Y or not prefer Party Y.
Independent: Sample size of 5 voters is less that 10% of the population(voters from the entire state)
Number of trials: There are a set number of trials (5) n=5
Same probability of success: p= 0.510
Calculator: P(x=2)= Binom (n=5, p=0.50, x=2) = 0.306
If 5 voters from the state are selected at random, the probability that exactly 2 of them prefer Party Y is 0.306.
Teacher Feedback
Small thing: for part a-ii, you provide the correct answer and use correct notation. However, you don’t show the numbers that go into the calculation, so on some rubrics that would be considered a “naked” answer in that you didn’t show the numbers along the way. Taking the extra step to show calculations with probability scenarios is always helpful. Everything else should receive full credit.
Student Response 5
a) i. P(county A and prefers party z)=.152 --> There’s a 15.2% chance that a person lives in county A and prefers party z.
ii. P(county A or prefers party z)= P(county A) + P(party z) - P(county A and party z) --> .4 + .31 - .152=.558 or 55.8% --> There’s a 55.8% chance that a person lives in county A or prefers party Z.
iii. P(county A|party z)= P(county A and party z)/P(party z) --> .152/.31=.49 --> There’s a 49% chance that the person lives in county A given that they prefer party Z.
b) P(Lives in county B|party x) --> P(county b and party x)/P(party x) = P(county B) <-- if this is true, the two events are independent
P(.108)/P(.18)=.6 which equals P(.6). This statement is true, which shows that these two events are independent of each other.
c) This is a binomial random variable because there is 2 outcomes for each trial – prefer party y (.51) or don’t prefer party y (.49). There is a set number of trials – 5 randomly selected voters from this state. The trials are independent of each other – seen in part b. Lastly, the probability of a success will not change in each trial (p=.51).
P(exactly 2/5 of randomly selected voters from the state prefer party y) = (5 2) = 5!/2!(5-2)! --> 10(.51)^2(.49)^3 = .306 --> There’s a 30.6% chance that exactly 2/5 of the randomly selected voters from the state prefer party Y.
Teacher Feedback
Nice job on your calculations (and super shout-out for going by hand - or at least writing it all out by hand - on the binomial calculations). Be really careful with your notation on part (b). Probability notation is kind of like function notation f(x) from algebra. The “stuff” inside the parentheses is like an input - and should represent what we’re finding the probability of. This will include variables and equality/inequality statements in some cases, but not just “plain numbers”, since those are the “output” in this situation. So P(.108) isn’t a thing - it should be P(B and X) = .108. That is, you already wrote the notations correctly - just put the actual numbers on your second line for part (b), and you’ll be good to go to say yes for independence.
Student Response 6
a) i) the probability that a person lives in country A and prefers party Z is 0.152
ii) the probability that a person lives in country A or prefers party Z is 0.4+0.31-0.152 = 0.558
iii) the probability that they live in country A given that they prefer party Z is 0.152/0.31 = 0.49032
b) for the events of living in country B and preferring party X to be independent the probability that a person lives in country B and the probability. that. they live in B given that. they prefer party X has to be equal. P(B) = 0.6 P(BㅣX) = 0.6549 since the probabilities are not equal, the two events are not independent.
c) binomial probability
binompdf (trials : 5, p : 0.51, x value : 2) = 0.306
Teacher Feedback
On part (a) and part ( c ), you’ve done all calculations correctly. For part (b), you’ve defined what we need to find to show independence… but your calculation P(B | X) is incorrect. You should get 0.108 / 0.18 = 0.6, so it would be independent. Double check what you did. Given what probability you got, you made an appropriate conclusion, so you’d still be eligible for partial credit.
Student Response 7
a) i) P(A∩Z)=0.152
ii) P(AUZ)=P(A)+P(Z)-P(A∩Z)=0.400+0.310-0.152=0.558
iii) P(AIZ)=P(A∩Z)/P(Z)=0.152/0.310=0.490323
b)When the situation is Independent P(A∩B)=P(A)×P(B)
0.108=0.600×0.180
So the events “Lives in County B” and “Prefers Party X” are Independent.
c) We know this is a Binomial Distribution since it’s Binary, Independent, & fixed number of trials.
binomCdf(n=5,p=0.510,x=2)=0.306005
Teacher Feedback
Good on all three parts!
Student Response 8
a.i. P(AandZ)=.152
ii. P(AorZ)=.400+.310-.152=.558
iii. P(AgivenZ)=.152/.31=.49
b. Yes they are independent because P(BandX)=.108 and P(B)*P(X)=.108. Since these two numbers are the same then the events are independent.
c. This is a binomial distribution because there is a success or failure as to whether the voters prefer Party Y or not, each voter chosen is independent of one another, Number of trials is fixed at 5, and there is a set number of probabilities for each choice. Binompdf(trials=5,p=.510,x=2)=.306
There is a .306 probability that exactly 2 of the 5 voters prefer Party Y.
Teacher Feedback
In part (b), you should do a little more to show where the P(B)*P(X) = 0.108 comes from. P(B and X) comes directly off the table so there’s no additional work to show, but P(B)*P(X) required a calculation, so you should show the numbers you multiplied. All other parts have appropriate work and correct answers.
Student Response 9
a. i. There is a 15.2% chance that the person lives in County A and prefers party Z
ii. There is a 55.8% chance that the person lives in County A or prefers Party Z.
iii. There is about a 49% chance that a person lives in County A, given that they prefer Party Z.
b. Yes, the events “Lives in County B” and “Prefers Party X” are independent. For two events to be independent, the P(A) must be equal to the P(A|B). The P(Lives in County B) is 60%, and then the P( Lives in County B | Prefers Party X)= .108/.18=.6=60%
c. P(X=2) = ( 5 2 )(.51)^2(1-.51)^5-2= .306
If 5 voters from the state are selected at random, the probability that exactly 2 of them prefer Party Y is 30.6%
Teacher Feedback
All answers are correct. However your work is not shown in part a-ii or a-iii, and should be, since it involved calculations of some kind. Anytime you need to add/subtract/multiply/divide to get an answer, you should show that work. Parts (b) and ( c ) show appropriate work.
Student Response 10
a. i.P(A and Z) = .152. There is a .152 probability that a randomly selected person lives in Country A and prefers Party Z.
ii. P(A or Z)= p(a) +p(z)- overlap or p(a and z) so .4+.310-.152 = .558. There is a .558 probability that a randomly selected person lives in Country A or prefers Party Z.
iii. P(a|z)= p(a and z) / P(z) or .152/.310 = .490. There is a .490 probability that a randomly selected person lives in Country A given that they prefer Party Z.
b. Independence means the probability of one variable is not affected if we know the other or in context P(lives in country B) = P(lives in country b|prefers party x)
P(b)= .6
P(b|x) = .108
.6 does not equal .108 so the events lives in country b and prefer party x are not independent.
c. P(2/5 prefer y)
n= 5 randomly selected people
p = .510 chance of success of preferring party y
x= 2 people exactly given to prefer party y
Each trial independent as same probability of success each time, fixed number of trials(5), and outcome is success or failure(person doesn’t prefer party y)
binompdf(5,.51,2)= .36. There is a .36 probability that exactly 2/5 voters selected at random prefer Party Y
Teacher Feedback
Solid work - in part (a), you give all probabilities correctly with supporting work. In part (b), you give the appropriate definition of independence, but unfortunately do not execute correctly - you gave P(b and x) and not P(b | x), which would be .108/.180 = 0.6… so the actual answer would be “yes”. You would get partial credit for defining independence, but making a mistake with execution. Part ( c) is all good.
Student Response 11
(a) (I would show all of the probability formulas for each question on paper during the test)
i. The probability that a person lives in County A and prefers Party Z is 0.152.
ii The probability that a person lives in County A or prefers Party Z is 0.4 + 0.31 - 0.152 = 0.558
iii. The probability that a person lives in County A given that they prefer Party Z is 0.152/0.31 = 0.49
(b) The events “lives in County B” and “Prefers Party X” are independent only if the probability of a person living in living in County B given that they prefer party X is equal to the probability of a person living in County B. The first probability is 0.108/0.180 = 0.6, while the second probability is 0.6. Since these two probabilities are equal, the events “lives in County B” and “Prefers Party X” are independent.
(C) This is an example of draw with replacement, where the party preference of voters is independent. Therefore, this is a binomial probability.
(5 choose 2 ) 0.510 ^ 2 * (1-0.510) ^ 3 = 0.3060 or 30.60 %
Teacher Feedback
Perfect! Full credit all around!
Student Response 12
a) i. P (A n Z) = 0.152
ii. P( A u Z) = .400+.310-.152= 0.558
iii. P (A|Z) = 0.152/0.310= 0.49032
B) Yes, they are independent because if P(B) * P(X) = P(B n X), that means that they are independent. And, in this scenario 0.6*0.180= 0.108, so it means that a person living in country B and preferring Party X is independent.
C)Checking for Binomial Distribution
2 Outcomes: Could prefer party y or could not (Good)
Independent Trials: Outcomes are independent of each other (Good)
Constant prob: The prob is constant ( 0.510) (Good)
Fixed Number of Trials (Good)
Can Use Binom Distribution
Calculation: P(Exactly 2 Prefer Y) = binompdf(n=5, p=0.510, x=2) = 0.306
Side note: I went ahead and did the conditions check, but it is necessary to provide it if we do get a question like this?
Teacher Feedback
Nice work! All parts have correct answers with work shown. If you do get asked a probability question that would require a binomial distribution (like part ( c )), you do not need to do a “conditions check”, as long as you clearly label the parameters for a binomial distribution. So something like “this scenario is binomial, with p = 0.510, n = 5 trials, and we want x = 2 successes.” [then show calculation] would get full credit. You only need to check the binomial conditions when explicitly asked if a binomial distribution is appropriate.
Student Response 13
a) i. P(A and Z) = 0.152
ii. P(A or Z) = P(A) + P(Z) - P(A and Z)
0.71-0.152=0.558
iii. P(A|Z) = P(A and Z)/P(A) = 0.152/0.4 = 0.38
b) Is P(B) equal to P(B|Z)?
P(B) = 0.6
P(X|B) = P(X and B)/P(X) = 0.108/0.18 = 0.6
Since the probability of preferring Party X given that they live in County B is equal to the probability of living County B, the events are independent.
c) This is a binomial distribution. There is success of failure because they either prefer Party Y or do not, there is a fixed number of trials (n = 5), each voter outcome is independent of one another, and there is a constant probability (p = 0.51) that the voter prefers Party Y.
binompdf (trials = 5, p = 0.51, successes = 2) = 0.306 probability that exactly 2 of the voters prefer Party Y.
Teacher Feedback
In part (a), you’ve correctly calculated the and / or probabilities, though you appear to have your conditional probability (the ‘given that’) probability backwards. The general formula is P(A | B) = P(A and B) / P(B); that is, the “given that” goes in the denominator. You put the wrong thing in the denominator, and so part (a) as a whole would be marked partially correct.
In part (b), check your notation - you mention P(B | Z) but the question asked about County X (you then go on to do the calculation involving X). You actually end up getting the right answer (“yes”), but it happens to be because you reversed the probability you should have been finding, P(B | X), into P(X | B), and then made the same reversal as in part a-iii, so you actually did end up calculating P(B | X) and reaching an appropriate conclusion. I’m not sure how something like this would be scored, but it would either get partial or no credit.
In part ( c ), you appropriately label the scenario as binomial, and execute the calculation correctly.
Student Response 14
a. i. P(A and Z) = .152
ii. P(a) + P(z) - P(a and z) = .400 + .310 - .152 = .558
iii. p(a given z) = .152/.310 = .49
b. p(b) = .6000/1 = .6
p(x) = .180/1 = .18
p(b) is not equal to p(x). .6 does not equal .18. These events are not independent.
c. Because this is a binomial distribution (party y = success, party x or z = failure, party preference is independent, and we want exactly 2 from party y), we can use binompdf
binompdf (trials = 5, p = .510, x-value = 2) = . 306 = .31
There is a .31 chance that exactly 2 out of the 5 randomly selected voters are in favor of Party Y.
Teacher Feedback
All work in parts (a) and ( c ) are correct. In part (b), you’ve got the right idea, but calculate the wrong probabilities - we should do P(b) and P(b|x) -or- P(x) and P(x|b). That is, one of the probabilities should be “regular” and the other should be “conditional” on the other variable. If THOSE are equal, then we’re independent.
AP Stats Practice FRQ Responses & Feedback (Unit 4)
14 min read•january 5, 2021
Jerry Kosoff
Jerry Kosoff
Practicing with FRQs is a great way to prep for the AP exam! Work through this prompt from Unit 3, then review student responses and corresponding feedback from Fiveable teacher Jerry Kosoff!
The Practice FRQ Prompt
A large group of voters in two nearby counties were surveyed about which political party they prefer between parties X, Y, and Z. The relative frequencies in the table below summarize the results of the survey.

a. If one surveyed person is selected at random:
i. What is the probability that the person lives in County A and prefers Party Z
ii. What is the probability that the person lives in County A or prefers Party Z?
iii. What is the probability that the person lives in County A, given that they prefer Party Z?
b. In the survey, are the events “Lives in County B” and “Prefers Party X” independent? Explain why or why not.
c. Assume that the distribution of party preference shown in the table holds true in the entire state. If 5 voters from the state are selected at random, what is the probability that exactly 2 of them prefer Party Y?
FRQ Writing Samples and Teacher Feedback
Student Response 1
a) i. P(County A and Party Z) = 0.152. There is a 0.152 probability that the person lives in County A and prefers Party Z.
ii) P(County A or Party Z) = P(County A) + P(Party Z) - P(County A and Party Z)
P(County A or Party Z) = 0.4 + 0.31 - 0.152 = 0.558. There is a 0.558 probability that the person lives in County A or prefers Party Z.
iii) P(County A|Party Z) = P(County A and Party Z) / P(Party Z) = 0.152 / 0.31 = 0.49. There is a 0.49 probability that the person lives in County A, given that they prefer Party Z.
b) If independent, P(Lives in County B and Prefers Party X) = P(Lives in County B) * P(Prefers Party X).
0.108 = 0.6 * 0.18 = 0.108
The events “Lives in County B” and “Prefers Party X” are independent, as the two events satisfy the multiplication rule for independent events.
c) Binomial Distribution Conditions - Binary - Party Y or not Party Y, Independent - reasonable to assume preferences of 5 voters are independent from each other, Number of Trials = 5 voters are selected at random (n=5), S = probability of selecting a voter who prefers Party Y is the same for every voter selected (p = 0.51)
X = the number of voters who prefer Party Y when the distribution of X is binomial with p = 0.51 and n = 5
P(X=2) = 0.306 using binomialpdf with p = 0.51, n = 5, and successes = 2.
There is a 0.306 probability that exactly two voters prefer Party Y if 5 voters from the state are selected at random.
Teacher Feedback
Well done! All three parts show strong command of statistical notation, and clear communication. Your answers are all correct and would all earn credit.
Student Response 2
a.) i. P(County A AND Party Z)= 0.152. There is a 15.2% chance that the person lives in County A and prefers Party Z.
ii.) P(County A OR Party Z)=0.400+0.310-0.152=0.558. There is a 55.8% chance that the person lives in County A or prefers Party Z
iii.) P(County A|Party Z)=0.152/0.310=0.490. There is a 49% chance that the person lives in County A given that they prefer Party Z.
b.) P(County B)= 0.600, P(County B|Party X)=0.108/0.180=0.60. Because the two probabilities are the same, the events “Live in County B” and “Prefers Party X” are independent.
c.) This scenario has each trial ends is either a success or failure, they are independent, the 2 selected are set, and the probability for those who prefer Party Y is the same at 0.510. Therefore, this is a binomial probability.
P(X=2)= BinomPDF(n=5, p=0.510, x=2)=0.306
There is a 30.6% chance that if 5 voters from the state are selected at random, exactly 2 of them will prefer Party Y.
Teacher Feedback
In all three parts, your answers are correct and presented with accompanying work and appropriate notation. You would get full credit for each part! Part ( c ) provides a good contrast to your work on Unit 4 FRQ #2 - by saying “the probability for those who prefer Party Y is the same at 0.510,” you provide an in-context reason for the scenario being binomial. Well done!
Student Response 3
A i. P(County A and Party Z)=.152/1=.152
ii. P(County A or Party Z)= .400+.310-.152=.558
iii. P(County A/Party Z)= .152/.310=.490
B. Yes, “lives in county B” and “prefers party x” are independent because:
P(County B/Party X)= P(County B): P(.6)= P(.600)
P(Party X/County B)= P(Party X): P(.18)= P(.180)
C. The probability that exactly 2 of them prefer Party Y is .306.
To find out I first check the binomial distribution requirements:
- Each trial has 2 possible outcomes (Party Y or not party Y)
- There are fixed number of trials (n=5)
- Outcomes are independent
- Probability of success is the same for each trial (p=.510)
I then proceeded to put on my calculator binompdf( 5, .510, 2). I knew to use the function binompdf because the problem is asking to find exactly 2 voters.
Teacher Feedback
All calculations and explanations are correct, with appropriate work shown. However, in part (b), you make a small notation error. P(County B | Party X) = P(County B) = 0.6. The probabilities themselves should not be inside the P( ) notation. Think of it like input/output function notation - inside the P( ) is what probability you’re finding (in words or symbols), while outside on the other side of the equals sign is the numerical answer.
Student Response 4
a i) The probability that a person lives in Country A and prefers Party Z is 0.152.
ii) The probability that the person lives in County A or prefers Party Z is 0.558.
P(AUB) = P(person lives in county A) + P(Person prefers Party Z) - P(person who lives in Country A and prefers Party Z)= 0.558
iii) P(Person lives in County A | Person prefers Party Z) = 0.152/0.310= 0.490
b) P(Living in County B)= 0.600 P(Living in County B | Prefers Party X)=0.108/ 0.180= 0.6
The events “Lives in County B” and "Prefers Party X"are independent as the probability of Living in County B equals the probability of living in county B given preferring Party X.
c. Binomial Distribution conditions:
Binary: Prefer Party Y or not prefer Party Y.
Independent: Sample size of 5 voters is less that 10% of the population(voters from the entire state)
Number of trials: There are a set number of trials (5) n=5
Same probability of success: p= 0.510
Calculator: P(x=2)= Binom (n=5, p=0.50, x=2) = 0.306
If 5 voters from the state are selected at random, the probability that exactly 2 of them prefer Party Y is 0.306.
Teacher Feedback
Small thing: for part a-ii, you provide the correct answer and use correct notation. However, you don’t show the numbers that go into the calculation, so on some rubrics that would be considered a “naked” answer in that you didn’t show the numbers along the way. Taking the extra step to show calculations with probability scenarios is always helpful. Everything else should receive full credit.
Student Response 5
a) i. P(county A and prefers party z)=.152 --> There’s a 15.2% chance that a person lives in county A and prefers party z.
ii. P(county A or prefers party z)= P(county A) + P(party z) - P(county A and party z) --> .4 + .31 - .152=.558 or 55.8% --> There’s a 55.8% chance that a person lives in county A or prefers party Z.
iii. P(county A|party z)= P(county A and party z)/P(party z) --> .152/.31=.49 --> There’s a 49% chance that the person lives in county A given that they prefer party Z.
b) P(Lives in county B|party x) --> P(county b and party x)/P(party x) = P(county B) <-- if this is true, the two events are independent
P(.108)/P(.18)=.6 which equals P(.6). This statement is true, which shows that these two events are independent of each other.
c) This is a binomial random variable because there is 2 outcomes for each trial – prefer party y (.51) or don’t prefer party y (.49). There is a set number of trials – 5 randomly selected voters from this state. The trials are independent of each other – seen in part b. Lastly, the probability of a success will not change in each trial (p=.51).
P(exactly 2/5 of randomly selected voters from the state prefer party y) = (5 2) = 5!/2!(5-2)! --> 10(.51)^2(.49)^3 = .306 --> There’s a 30.6% chance that exactly 2/5 of the randomly selected voters from the state prefer party Y.
Teacher Feedback
Nice job on your calculations (and super shout-out for going by hand - or at least writing it all out by hand - on the binomial calculations). Be really careful with your notation on part (b). Probability notation is kind of like function notation f(x) from algebra. The “stuff” inside the parentheses is like an input - and should represent what we’re finding the probability of. This will include variables and equality/inequality statements in some cases, but not just “plain numbers”, since those are the “output” in this situation. So P(.108) isn’t a thing - it should be P(B and X) = .108. That is, you already wrote the notations correctly - just put the actual numbers on your second line for part (b), and you’ll be good to go to say yes for independence.
Student Response 6
a) i) the probability that a person lives in country A and prefers party Z is 0.152
ii) the probability that a person lives in country A or prefers party Z is 0.4+0.31-0.152 = 0.558
iii) the probability that they live in country A given that they prefer party Z is 0.152/0.31 = 0.49032
b) for the events of living in country B and preferring party X to be independent the probability that a person lives in country B and the probability. that. they live in B given that. they prefer party X has to be equal. P(B) = 0.6 P(BㅣX) = 0.6549 since the probabilities are not equal, the two events are not independent.
c) binomial probability
binompdf (trials : 5, p : 0.51, x value : 2) = 0.306
Teacher Feedback
On part (a) and part ( c ), you’ve done all calculations correctly. For part (b), you’ve defined what we need to find to show independence… but your calculation P(B | X) is incorrect. You should get 0.108 / 0.18 = 0.6, so it would be independent. Double check what you did. Given what probability you got, you made an appropriate conclusion, so you’d still be eligible for partial credit.
Student Response 7
a) i) P(A∩Z)=0.152
ii) P(AUZ)=P(A)+P(Z)-P(A∩Z)=0.400+0.310-0.152=0.558
iii) P(AIZ)=P(A∩Z)/P(Z)=0.152/0.310=0.490323
b)When the situation is Independent P(A∩B)=P(A)×P(B)
0.108=0.600×0.180
So the events “Lives in County B” and “Prefers Party X” are Independent.
c) We know this is a Binomial Distribution since it’s Binary, Independent, & fixed number of trials.
binomCdf(n=5,p=0.510,x=2)=0.306005
Teacher Feedback
Good on all three parts!
Student Response 8
a.i. P(AandZ)=.152
ii. P(AorZ)=.400+.310-.152=.558
iii. P(AgivenZ)=.152/.31=.49
b. Yes they are independent because P(BandX)=.108 and P(B)*P(X)=.108. Since these two numbers are the same then the events are independent.
c. This is a binomial distribution because there is a success or failure as to whether the voters prefer Party Y or not, each voter chosen is independent of one another, Number of trials is fixed at 5, and there is a set number of probabilities for each choice. Binompdf(trials=5,p=.510,x=2)=.306
There is a .306 probability that exactly 2 of the 5 voters prefer Party Y.
Teacher Feedback
In part (b), you should do a little more to show where the P(B)*P(X) = 0.108 comes from. P(B and X) comes directly off the table so there’s no additional work to show, but P(B)*P(X) required a calculation, so you should show the numbers you multiplied. All other parts have appropriate work and correct answers.
Student Response 9
a. i. There is a 15.2% chance that the person lives in County A and prefers party Z
ii. There is a 55.8% chance that the person lives in County A or prefers Party Z.
iii. There is about a 49% chance that a person lives in County A, given that they prefer Party Z.
b. Yes, the events “Lives in County B” and “Prefers Party X” are independent. For two events to be independent, the P(A) must be equal to the P(A|B). The P(Lives in County B) is 60%, and then the P( Lives in County B | Prefers Party X)= .108/.18=.6=60%
c. P(X=2) = ( 5 2 )(.51)^2(1-.51)^5-2= .306
If 5 voters from the state are selected at random, the probability that exactly 2 of them prefer Party Y is 30.6%
Teacher Feedback
All answers are correct. However your work is not shown in part a-ii or a-iii, and should be, since it involved calculations of some kind. Anytime you need to add/subtract/multiply/divide to get an answer, you should show that work. Parts (b) and ( c ) show appropriate work.
Student Response 10
a. i.P(A and Z) = .152. There is a .152 probability that a randomly selected person lives in Country A and prefers Party Z.
ii. P(A or Z)= p(a) +p(z)- overlap or p(a and z) so .4+.310-.152 = .558. There is a .558 probability that a randomly selected person lives in Country A or prefers Party Z.
iii. P(a|z)= p(a and z) / P(z) or .152/.310 = .490. There is a .490 probability that a randomly selected person lives in Country A given that they prefer Party Z.
b. Independence means the probability of one variable is not affected if we know the other or in context P(lives in country B) = P(lives in country b|prefers party x)
P(b)= .6
P(b|x) = .108
.6 does not equal .108 so the events lives in country b and prefer party x are not independent.
c. P(2/5 prefer y)
n= 5 randomly selected people
p = .510 chance of success of preferring party y
x= 2 people exactly given to prefer party y
Each trial independent as same probability of success each time, fixed number of trials(5), and outcome is success or failure(person doesn’t prefer party y)
binompdf(5,.51,2)= .36. There is a .36 probability that exactly 2/5 voters selected at random prefer Party Y
Teacher Feedback
Solid work - in part (a), you give all probabilities correctly with supporting work. In part (b), you give the appropriate definition of independence, but unfortunately do not execute correctly - you gave P(b and x) and not P(b | x), which would be .108/.180 = 0.6… so the actual answer would be “yes”. You would get partial credit for defining independence, but making a mistake with execution. Part ( c) is all good.
Student Response 11
(a) (I would show all of the probability formulas for each question on paper during the test)
i. The probability that a person lives in County A and prefers Party Z is 0.152.
ii The probability that a person lives in County A or prefers Party Z is 0.4 + 0.31 - 0.152 = 0.558
iii. The probability that a person lives in County A given that they prefer Party Z is 0.152/0.31 = 0.49
(b) The events “lives in County B” and “Prefers Party X” are independent only if the probability of a person living in living in County B given that they prefer party X is equal to the probability of a person living in County B. The first probability is 0.108/0.180 = 0.6, while the second probability is 0.6. Since these two probabilities are equal, the events “lives in County B” and “Prefers Party X” are independent.
(C) This is an example of draw with replacement, where the party preference of voters is independent. Therefore, this is a binomial probability.
(5 choose 2 ) 0.510 ^ 2 * (1-0.510) ^ 3 = 0.3060 or 30.60 %
Teacher Feedback
Perfect! Full credit all around!
Student Response 12
a) i. P (A n Z) = 0.152
ii. P( A u Z) = .400+.310-.152= 0.558
iii. P (A|Z) = 0.152/0.310= 0.49032
B) Yes, they are independent because if P(B) * P(X) = P(B n X), that means that they are independent. And, in this scenario 0.6*0.180= 0.108, so it means that a person living in country B and preferring Party X is independent.
C)Checking for Binomial Distribution
2 Outcomes: Could prefer party y or could not (Good)
Independent Trials: Outcomes are independent of each other (Good)
Constant prob: The prob is constant ( 0.510) (Good)
Fixed Number of Trials (Good)
Can Use Binom Distribution
Calculation: P(Exactly 2 Prefer Y) = binompdf(n=5, p=0.510, x=2) = 0.306
Side note: I went ahead and did the conditions check, but it is necessary to provide it if we do get a question like this?
Teacher Feedback
Nice work! All parts have correct answers with work shown. If you do get asked a probability question that would require a binomial distribution (like part ( c )), you do not need to do a “conditions check”, as long as you clearly label the parameters for a binomial distribution. So something like “this scenario is binomial, with p = 0.510, n = 5 trials, and we want x = 2 successes.” [then show calculation] would get full credit. You only need to check the binomial conditions when explicitly asked if a binomial distribution is appropriate.
Student Response 13
a) i. P(A and Z) = 0.152
ii. P(A or Z) = P(A) + P(Z) - P(A and Z)
0.71-0.152=0.558
iii. P(A|Z) = P(A and Z)/P(A) = 0.152/0.4 = 0.38
b) Is P(B) equal to P(B|Z)?
P(B) = 0.6
P(X|B) = P(X and B)/P(X) = 0.108/0.18 = 0.6
Since the probability of preferring Party X given that they live in County B is equal to the probability of living County B, the events are independent.
c) This is a binomial distribution. There is success of failure because they either prefer Party Y or do not, there is a fixed number of trials (n = 5), each voter outcome is independent of one another, and there is a constant probability (p = 0.51) that the voter prefers Party Y.
binompdf (trials = 5, p = 0.51, successes = 2) = 0.306 probability that exactly 2 of the voters prefer Party Y.
Teacher Feedback
In part (a), you’ve correctly calculated the and / or probabilities, though you appear to have your conditional probability (the ‘given that’) probability backwards. The general formula is P(A | B) = P(A and B) / P(B); that is, the “given that” goes in the denominator. You put the wrong thing in the denominator, and so part (a) as a whole would be marked partially correct.
In part (b), check your notation - you mention P(B | Z) but the question asked about County X (you then go on to do the calculation involving X). You actually end up getting the right answer (“yes”), but it happens to be because you reversed the probability you should have been finding, P(B | X), into P(X | B), and then made the same reversal as in part a-iii, so you actually did end up calculating P(B | X) and reaching an appropriate conclusion. I’m not sure how something like this would be scored, but it would either get partial or no credit.
In part ( c ), you appropriately label the scenario as binomial, and execute the calculation correctly.
Student Response 14
a. i. P(A and Z) = .152
ii. P(a) + P(z) - P(a and z) = .400 + .310 - .152 = .558
iii. p(a given z) = .152/.310 = .49
b. p(b) = .6000/1 = .6
p(x) = .180/1 = .18
p(b) is not equal to p(x). .6 does not equal .18. These events are not independent.
c. Because this is a binomial distribution (party y = success, party x or z = failure, party preference is independent, and we want exactly 2 from party y), we can use binompdf
binompdf (trials = 5, p = .510, x-value = 2) = . 306 = .31
There is a .31 chance that exactly 2 out of the 5 randomly selected voters are in favor of Party Y.
Teacher Feedback
All work in parts (a) and ( c ) are correct. In part (b), you’ve got the right idea, but calculate the wrong probabilities - we should do P(b) and P(b|x) -or- P(x) and P(x|b). That is, one of the probabilities should be “regular” and the other should be “conditional” on the other variable. If THOSE are equal, then we’re independent.

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.