
8.7 Volumes with Cross Sections: Squares and Rectangles
5 min read•february 15, 2024
So far in this unit, you’ve been learning how to find the area between two curves. However, we can also use these curves to represent a three-dimensional object. In this guide, you’ll learn how to find the volume of this object.
🪩 Solids with Cross Sections
When we want to find the volume of a three-dimensional object, particularly those difficult to calculate with geometry, we can instead break it up into infinitely thin slices that are easier to work with. To find the volume of a solid with known cross-sections we can use the formula:
where is a function for the area of a cross-section (some two-dimensional shape) perpendicular to the x-axis on the closed interval and represents its thickness.
🔲 Square Cross Sections
To find a shape using square cross sections, we’ll use the formula for . Plugging this into our initial equation, we find that the formula for the volume of a solid with square cross sections is
It’s important to note here that we’re taking the volume of rectangular prisms—it’s just that the thickness is infinitely thin, represented by .
🔳 Rectangular Cross Sections
To find the area of a rectangle, we use the formula where is the width of the rectangle and is the height. So the formula for the volume of a soil with rectangular cross sections is given by . Remember, is your thickness!
✏️ Solving Cross-Section Problems
🤔 Now that we have these formulas, how do we figure out what , , or are so that we can use them? Let’s work through an example.
Example 1: Solids with Square Cross Sections
Suppose a region bounded by and forms the base of a solid and each cross section perpendicular to the 𝑥-axis is a square. What is the volume of the solid?
Question courtesy of Flipped Math
Since this solid has square cross sections, we know that we’ll use the formula .
💭 We’ll begin by visualizing the problem. A picture of the graphs may or may not be given on the AP exam, but can be very useful to start to understand the problem and to make sure you’re using the correct bounds. You can also sketch the graph of a problem to help you work it out!
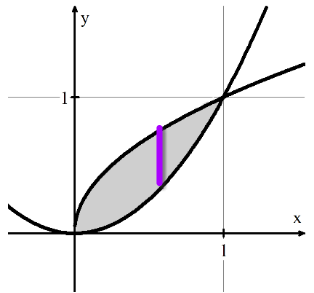
Image courtesy of Flipped Math
In this image, forms the upper curve, and is the bottom curve. Let’s let function and . The area in grey is the base of our solid. The purple line represents a singular cross section of this solid. You can imagine that the cross section is coming towards you along a z-axis not shown in this drawing. If we rotated our graph and included the z-axis, our graph would look something like this:
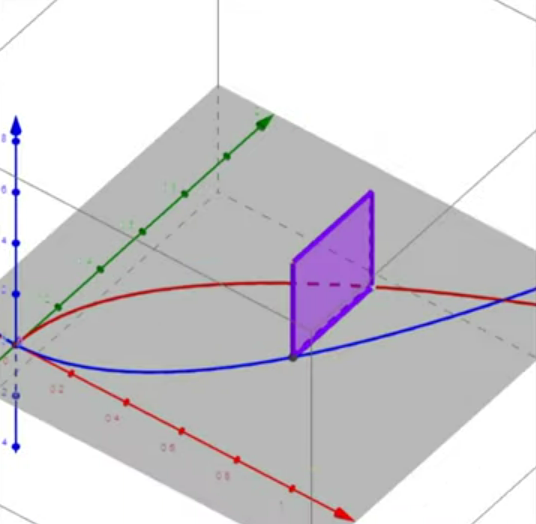
Image courtesy of Flipped Math
You’ll notice that the length of one side of our square at any given is given by the difference between our upper curve, , and our lower curve, . This means that .
Next, let’s identify our bounds. Graphically, we can see that the two functions intersect for and . This means that our bounds are given by the closed interval [0, 1]. We could also find the bounds algebraically by setting the two functions equal and solving for x as shown below:
Now that we have our bounds and our function for , we can plug these into our formula to find the volume of this solid is given by . Using your favorite methods to solve definite integrals, you should find that the volume of this solid is or about 0.1285.
Need to see the steps?
First, solve for the integral.
Then, evaluate over the bounds.
Example 2: Solids with Rectangular Cross Sections
The base of a solid is bounded by , , and . Find the volume if the cross sections, taken perpendicular to the y-axis, form a rectangle whose height is 6.
Question courtesy of Flipped Math
☝️There are a couple important differences to notice here as compared with the last example. In this question, we are taking cross sections perpendicular to the y-axis instead of the x-axis. We’ve also been given three functions to define our bounds. Since our cross sections are rectangular, we’ll also need to use our other equation to find the volume of the solid. Since we are working perpendicular to the y-axis, our integral is integrated with respect to , not .
👀Let’s begin again by visualizing our problem.
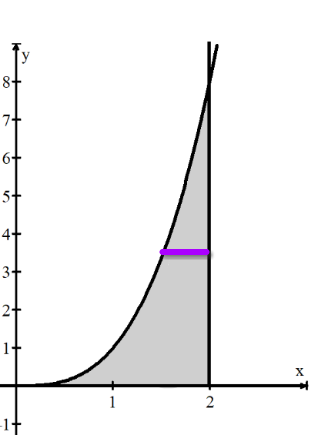
Image Course of Flipped Math.
In this image, forms our left curve, and forms our right curve. A purple line represents our cross section perpendicular to the y-axis. To find the width of one of the rectangles for a given (remember, we’re working with respect to the y-axis!), we need to evaluate our functions and for our chosen value. This second equation can be re-written in terms of so it is easier to use as . This gives us . Our problem tells us that the height of these rectangles is always 6, so
Now we need to find our bounds. We can see that the two graphs intersect at , but they don’t intersect at any other point, as the function will only equal 2 once. This is where our third equation comes in. The problem tells us that the solid is also bounded by the function . This means that our bounds are [0, 8]. Plugging everything into our formula we find . Solving this definite integral, you should find that the volume of this solid is 24.
Great work! 🍀
✏️ Summary
When finding the volume of a solid with a known cross section, we can use the equation…
is a function for the area of a cross section perpendicular to the x-axis on the interval [a, b].
For square cross sections, where is the length of one of the square’s sides.
For rectangular cross sections, where is the rectangle’s width and is its height.
Using methods for finding the areas between curves we can determine equations to describe or and and find bounds for our integral.
Plugging in our bounds, function and solving the resultant integral yields the volume of our solid.
8.7 Volumes with Cross Sections: Squares and Rectangles
5 min read•february 15, 2024
So far in this unit, you’ve been learning how to find the area between two curves. However, we can also use these curves to represent a three-dimensional object. In this guide, you’ll learn how to find the volume of this object.
🪩 Solids with Cross Sections
When we want to find the volume of a three-dimensional object, particularly those difficult to calculate with geometry, we can instead break it up into infinitely thin slices that are easier to work with. To find the volume of a solid with known cross-sections we can use the formula:
where is a function for the area of a cross-section (some two-dimensional shape) perpendicular to the x-axis on the closed interval and represents its thickness.
🔲 Square Cross Sections
To find a shape using square cross sections, we’ll use the formula for . Plugging this into our initial equation, we find that the formula for the volume of a solid with square cross sections is
It’s important to note here that we’re taking the volume of rectangular prisms—it’s just that the thickness is infinitely thin, represented by .
🔳 Rectangular Cross Sections
To find the area of a rectangle, we use the formula where is the width of the rectangle and is the height. So the formula for the volume of a soil with rectangular cross sections is given by . Remember, is your thickness!
✏️ Solving Cross-Section Problems
🤔 Now that we have these formulas, how do we figure out what , , or are so that we can use them? Let’s work through an example.
Example 1: Solids with Square Cross Sections
Suppose a region bounded by and forms the base of a solid and each cross section perpendicular to the 𝑥-axis is a square. What is the volume of the solid?
Question courtesy of Flipped Math
Since this solid has square cross sections, we know that we’ll use the formula .
💭 We’ll begin by visualizing the problem. A picture of the graphs may or may not be given on the AP exam, but can be very useful to start to understand the problem and to make sure you’re using the correct bounds. You can also sketch the graph of a problem to help you work it out!

Image courtesy of Flipped Math
In this image, forms the upper curve, and is the bottom curve. Let’s let function and . The area in grey is the base of our solid. The purple line represents a singular cross section of this solid. You can imagine that the cross section is coming towards you along a z-axis not shown in this drawing. If we rotated our graph and included the z-axis, our graph would look something like this:

Image courtesy of Flipped Math
You’ll notice that the length of one side of our square at any given is given by the difference between our upper curve, , and our lower curve, . This means that .
Next, let’s identify our bounds. Graphically, we can see that the two functions intersect for and . This means that our bounds are given by the closed interval [0, 1]. We could also find the bounds algebraically by setting the two functions equal and solving for x as shown below:
Now that we have our bounds and our function for , we can plug these into our formula to find the volume of this solid is given by . Using your favorite methods to solve definite integrals, you should find that the volume of this solid is or about 0.1285.
Need to see the steps?
First, solve for the integral.
Then, evaluate over the bounds.
Example 2: Solids with Rectangular Cross Sections
The base of a solid is bounded by , , and . Find the volume if the cross sections, taken perpendicular to the y-axis, form a rectangle whose height is 6.
Question courtesy of Flipped Math
☝️There are a couple important differences to notice here as compared with the last example. In this question, we are taking cross sections perpendicular to the y-axis instead of the x-axis. We’ve also been given three functions to define our bounds. Since our cross sections are rectangular, we’ll also need to use our other equation to find the volume of the solid. Since we are working perpendicular to the y-axis, our integral is integrated with respect to , not .
👀Let’s begin again by visualizing our problem.

Image Course of Flipped Math.
In this image, forms our left curve, and forms our right curve. A purple line represents our cross section perpendicular to the y-axis. To find the width of one of the rectangles for a given (remember, we’re working with respect to the y-axis!), we need to evaluate our functions and for our chosen value. This second equation can be re-written in terms of so it is easier to use as . This gives us . Our problem tells us that the height of these rectangles is always 6, so
Now we need to find our bounds. We can see that the two graphs intersect at , but they don’t intersect at any other point, as the function will only equal 2 once. This is where our third equation comes in. The problem tells us that the solid is also bounded by the function . This means that our bounds are [0, 8]. Plugging everything into our formula we find . Solving this definite integral, you should find that the volume of this solid is 24.
Great work! 🍀
✏️ Summary
When finding the volume of a solid with a known cross section, we can use the equation…
is a function for the area of a cross section perpendicular to the x-axis on the interval [a, b].
For square cross sections, where is the length of one of the square’s sides.
For rectangular cross sections, where is the rectangle’s width and is its height.
Using methods for finding the areas between curves we can determine equations to describe or and and find bounds for our integral.
Plugging in our bounds, function and solving the resultant integral yields the volume of our solid.

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.