PSAT: Complete Guide to the Math Section

What is the PSAT/NMSQT and why is it important?

The Preliminary SAT, or PSAT, is a practice exam that can be used as a simulation for the real SAT taken as a junior or senior.

The PSAT can be taken as early as eighth or ninth grade (PSAT 8/9). There is also one offered in tenth grade (PSAT 10).

The PSAT taken in October of 11th grade is considered especially important because this PSAT is used as the NMSQT, or National Merit Scholarship Qualifying Test. After the test, students will receive a Selection Index score in their senior year. Different states have different cutoff scores. If students score in the top 3-4% but don’t meet the cutoff score, they are considered Commended Students. Students who score in the top 1% of test takers become Semifinalists (around 16,000 students total) and a majority of those students go on to become Finalists, which gives them a chance to earn scholarship money from the National Merit Scholarship Corporation or colleges that give scholarships based on NMSQT scores (Learn More).

Either way, the PSAT makes great practice for the SAT, one of the main two tests that are used to indicate college readiness during the college admission processes.

What are the sections in the PSAT?

There are 4 sections on the test. These are:

1. Reading Test 📚
2. Writing and Language Test 📝
3. Math Test - Calculator 🧮
4. Math Test - No Calculator ➗

The PSAT is out 1520 (whereas the SAT is out of 1600). Math is 760 out the total 1520 points, which means it comprises 50% of the sections on the PSAT, making it an essential subject to review before the test. In this study guide, we will go over the logistics of the two math sections, strategies to improve accuracy and speed, and review important content to help you ace the math section. 💪🏾

Overview of the Math Sections

In both sections, students will be provided the following formula sheet.

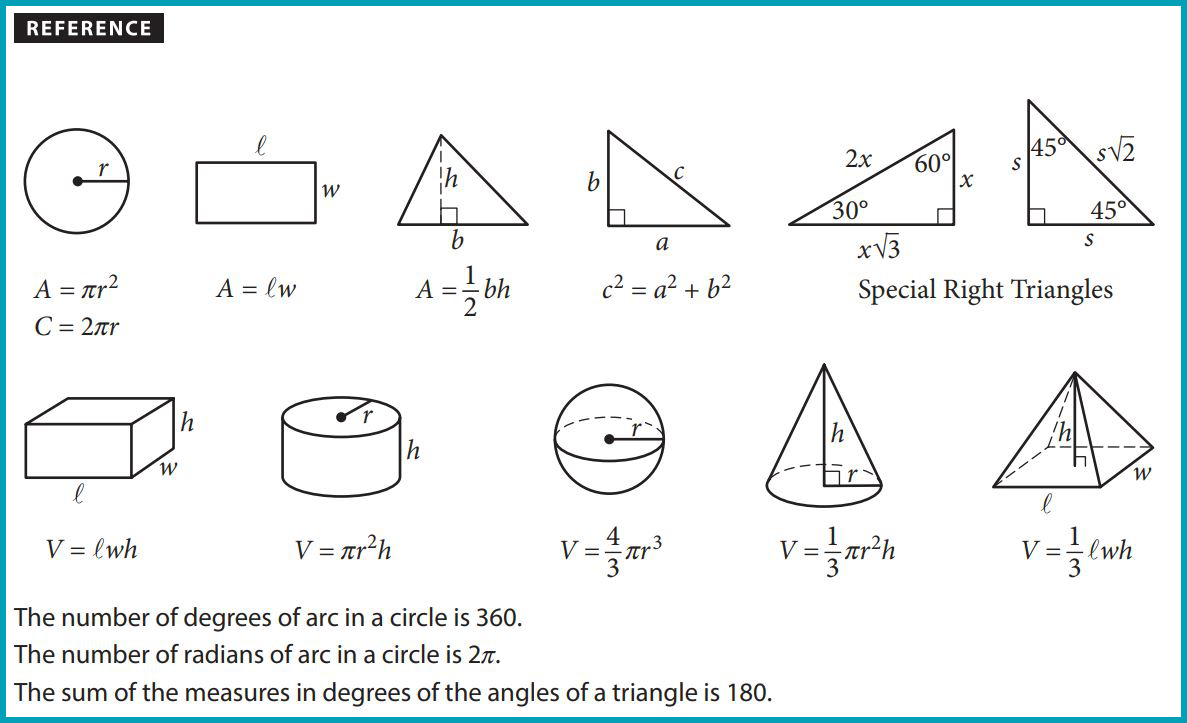
Timing and Length of Each Test

Math Test - No Calculator:

• 25 minutes
• 17 questions
• 13 multiple choice questions (MCQs)
• 4 Grid-Ins (GIs)

Math Test - Calculator:

• 45 minutes
• 31 questions
• 27 multiple choice questions (MCQs)
• 4 Grid-Ins (GIs)

Strategies for PSAT Math

These are also very useful for the regular ol’ SAT.

Process of Elimination

When you take the test and you stumble upon a challenging question, eliminate choices that you know for certain aren’t correct. For example, you eliminate C and D, leaving A and B. Now there is a 50% chance of getting the answer correct, even if you have to guess. REMEMBER that there is no penalty for an incorrect answer. Therefore, make the best guess you can and move on to the next question.

Move On Already

There are 17 questions on the non-calculator section. Imagine if you spent like 5 out of the 25 allotted minutes on a difficult question. Now you only have 20 minutes to do the other 16 questions. 😬 Unfortunately, you are only able to finish 12 of those questions. This results with you getting 76% on this section. However, if you had just marked the question for later or guessed on it, you would have potentially gotten 94% on this section. Therefore, being cognizant of which questions are taking a significant amount of time is very important. After all, the questions are weighted the same. The hard questions don’t earn more points, so don't get stuck wasting time on them.

When all else fails, pick C

Just joking. It doesn’t have to be C. The point is to pick a letter that you will use as a default for whenever you can’t answer a question. The first option, of course, would be to make an educated guess. But if you still have no clue, just bubble in the same letter for all the unsure questions to increase your probability of getting each question right.

Read the question (Obviously, Right?)

Sometimes we are in such a rush that we forget to read the whole question. For example, the question asks “if x satisfies the equation above, what is the value of _x + _." You might be in a hurry and quickly solve for the value of x, rather than understanding what the question is truly asking. There are often multi-step problems like this that get missed due to not reading till the end. This common mistake is often made on problems like the statistical table ones where they are asking for conditional frequency not relative frequency.

Familiarize yourself on how to fill out grid for the Grid-In answers

There are two reasons for this. A-you don’t want to waste time reading how you’re supposed to input answers on the day of the test. B-you don’t want your answers to be read wrong by the scantron. 🤦🏿‍♀️

Here are the tips (besides the basics):

• Don’t worry about your handwriting when you are writing the answer in the box (the bubbles are graded). It’s not even required, though it helps with alignment.
• Be careful about mixed numbers. If you meant "4 and one-fifths" , but you input 4 1 / 5 on the grid, it will be scanned as "41 over 5". Therefore, convert into a decimal (4.2) or an improper fraction (21/5).
• Decimals answers exceeding the grid should be rounded or cut off to fill the entire grid. Questions will usually ask for you to round to a certain place to avoid confusion.

Sketch it out

This is especially useful for when there is a problem in which you have to visualize a graph. For example, the problem gives two points that an equation (7x + b) goes through and asks for the value of b (the y-intercept). It helps to visualize it a bit to understand the ballpark of where the answers should be valued.

Plug it in!

There are two ways you can do this. Either you plug the answer choices into the provided equations (or inequality) OR you plug a random number into each answer choice to find the equation that satisfies the conditions of the question.

For example, you need to select the correct order pair that satisfies a system of equations. You can just plug the ordered pairs in and see if the left and right sides of the equation match for both equations in the system, then you got your answer! ✔️

Plugging a number into an equation or inequality usually works when there is a question that asks for some equivalent equation or to write an equation that satisfies certain conditions.

Take notes

There are often multi-step problems with a lot of information to process at once. Therefore, you should take little notes on the side for each significant number that is given. Ask yourself: what information do I KNOW and what exactly is it that I'm looking for? This way, you have broken the problem down into bits of information that you can easily process to solve the problem.

Underline

A good technique is to underline important numbers as you read the question. This technique is especially important for problems relating to unit conversions/rates. Underline the unit that the answer should be in and keep this on the back of your mind as you solve the problem. For example, the question asks for something in ounces, but you have been solving the problem in gallons and you didn’t convert. Yikes! 😱

Unit Conversion Hack

This trick is often taught in science classrooms, but it's very useful for the PSAT as well.

1. Write the value and units of the number you are given or have just solved for.

5 gallons

2. Write this as a fraction over 1.

5 gallons / 1

3. Multiply it by the conversion factor (often provided in the problem). This conversion factor should be a fraction with the unit that YOU WANT in the answer in the numerator and the unit that you are converting FROM in the denominator.

(5 gallons / 1 ) * (128 ounces / 1 )

4. Repeat Step 3 until you get to the type of units you desire

5. Multiply all the fractions out and get your answer!

640 ounces

Calculator Hacks (TI-84 edition)

• When solving to find solution to a quadratic equation, just graph it to find the zeroes (the x-intercepts).
• When finding the solutions to a system of equations, graph the equations and look for the intersection points.
• Convert your decimal into a fraction (if needed) by pressing the "MATH" key and then "1" key.
• Though you can use the TI-84 for unit conversion, it's best to use the conversion factors given in the problem.
• When a problem asks for an answer in radians, make sure your calculator is in "RADIAN" mode (it shows on top). Just press "mode", highlight "radian", press "enter", press "2nd", and then press "mode" to change from "DEGREE" to "RADIAN".

Types of questions on PSAT Math sections

According to the College Board, the main 3 topics that are tested in these sections are the Heart of Algebra, Problem Solving and Data Analysis, and Passport to Advanced Math. There are also some additional topics. We have provided examples of problems for each type of question.

Heart of Algebra (16 questions)

Linear equations/inequalities

Solve for a variable in the linear equation/inequality, write a linear expression or equation/inequality depending on the context of the problem, simplifying equations/inequalities, or interpreting an equation/inequality in a word problem.

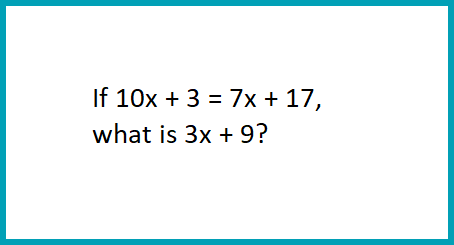
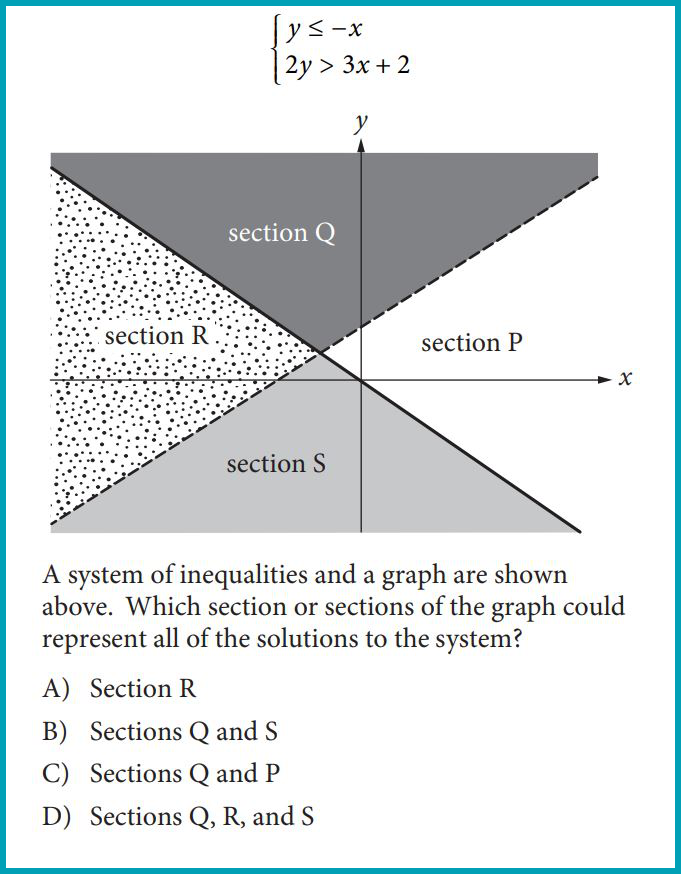
Systems of two linear equations/inequalities with two variables

Write or interpret a system of equations/inequalities depending on the context of the problem, and solve/simplify the system.

Write a linear function based on the linear relationship between two quantities

The function should have two variables and is formed from data given from the word problem.

Solve linear equations/inequalities with one variable (ex. 2x + 3 = 30)

The equation can have 0, 1, or an infinite # of solutions. Determining what value a constant or coefficient in an equation should have to yield 0 or infinite # of solutions.

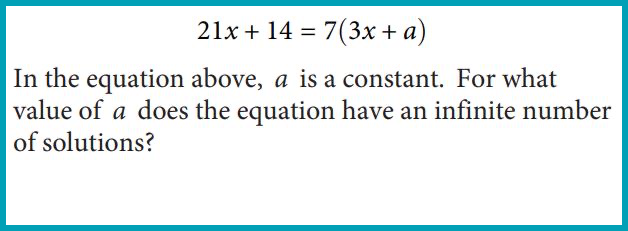
Solve two-equation systems with two variables algebraically (ex. 2x + 3y = 30)

The system can have 0, 1, 2, or infinite # of solutions. Determining what value a constant or coefficient in an equation should have to yield 0, 1, or infinite # of solutions.

Connection between equations and real-life context

Given context about a situation, interpret what the constants and variables in an equation mean.

Relationship between algebraic and graphical representations of a linear equation

Select a graph depending on given equation (or vice versa), evaluate how changes in the equation result in changes in the corresponding graph, write the equation of a line given description about its graph, and understand important graph features (like the y-intercept, x-intercept, and slope) based on the given equation.

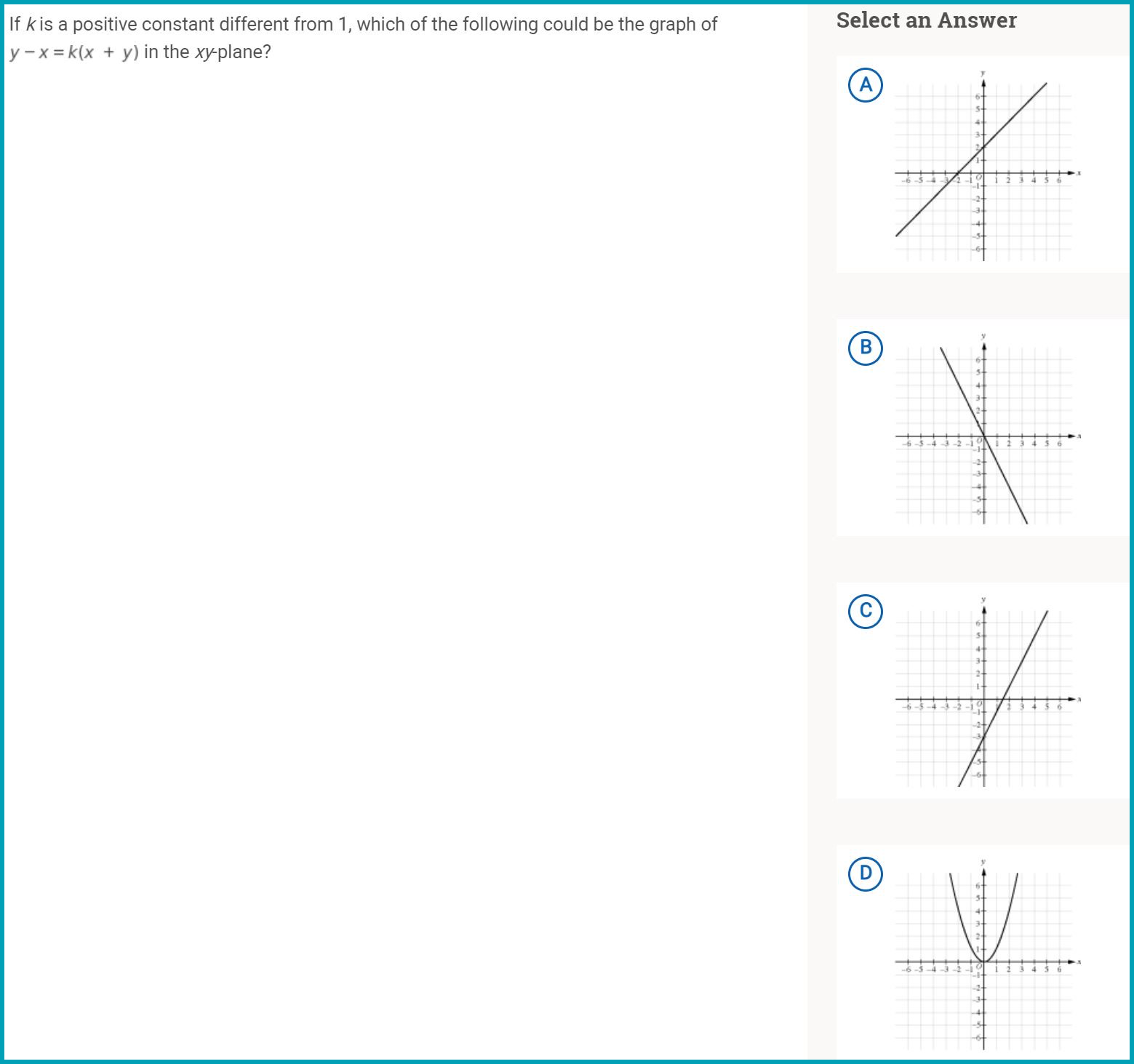
Problem Solving and Data Analysis (16 questions)

Ratios/Proportions/Rate

Know how to calculate ratios/rates from a proportional relationship between two quantities.

Percentages

Know how to calculate and/or use percentages to solve word problems. A commonly asked question is when there are some items on that get a "20 %". You are either asked to find the original price or the new price.

Unit Conversions

Know how to calculate density and use it for solving a problem. Also, know how to perform unit conversions and determine unit rates. These problems won't be straight-up conversions though. They are often multiple conversions and multiple steps.

‍

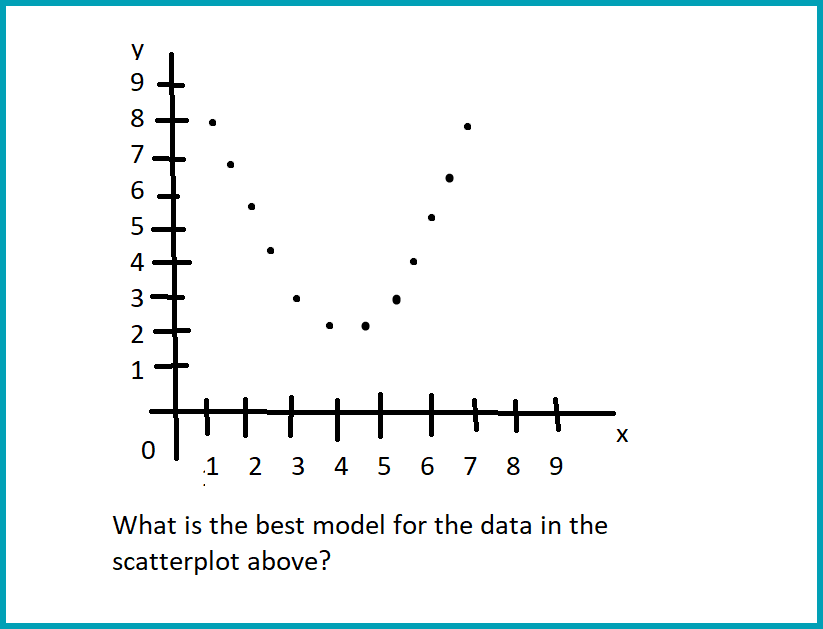
Scatterplots

Select the linear, quadratic, or exponential equation that best correlates to the given scatterplot (line/curve of best fit). Understand the meaning of the line in relation to the situational context and be able to make a prediction using the line/curve of best fit.

Relationship between two variables and the graph

Given the properties described by the problem, find a graph that suits those properties (ex. x-intercepts are 0 and 3). Use the graph to estimate values (ex. Find the slope).

Linear growth vs exponential growth

Know the differences between these two models of growth when solving problems.

Categorical Data (the stats questions!)

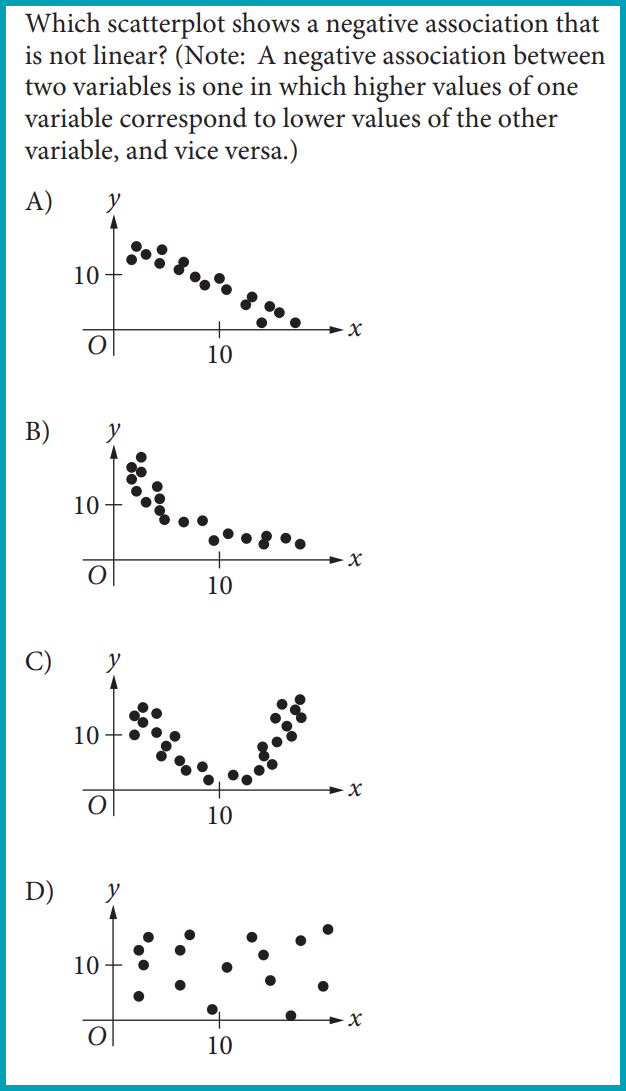
Interpret two-way tables and/or calculate relative frequencies (ex. Out of 100 girls, 10 girls liked butter pecan ice cream. The relative frequency would be 1/10 or 10%), conditional frequencies (ex. Out of the students that are seniors, what is the percentage of picking a person who likes sushi), conditional probabilities (ex. If we know that an odd number was picked from 1-10, then what is the probability of getting a 7?), positive/negative association of variables (Ex. Is the scatterplot going up and right? If yes, then positive association). If it is going down and right, it is a negative association.), and independent events (These are events that don’t affect the outcome of another event. An event is just a set of outcomes and can be anything like rolling a number greater than 4).

‍

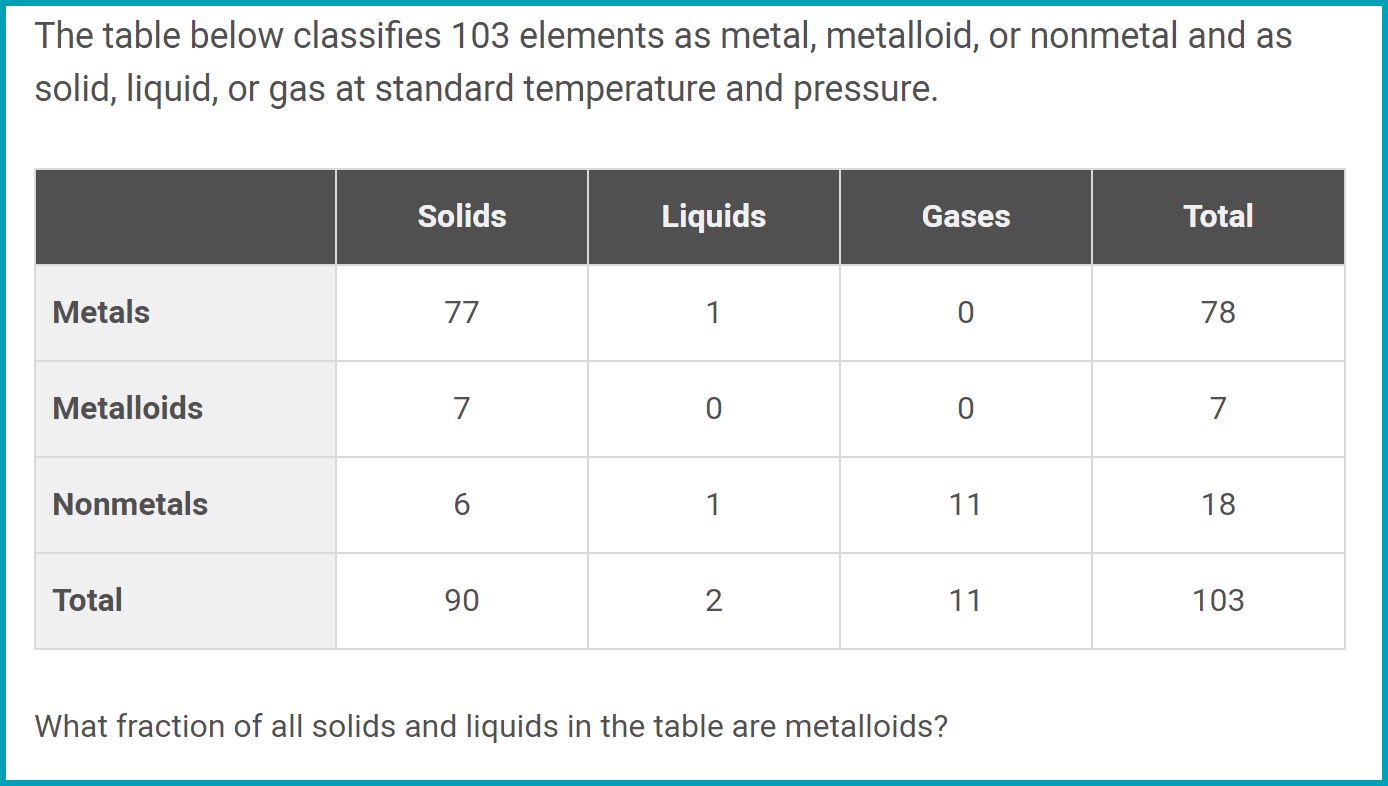
Inferences about population parameters from sample data

Sounds very technical right? Based on the sample data, make an inference about what the population parameters (mean, median, mode, range) will be. Confidence intervals and measurement error may be mentioned but do not need to be calculated.

‍

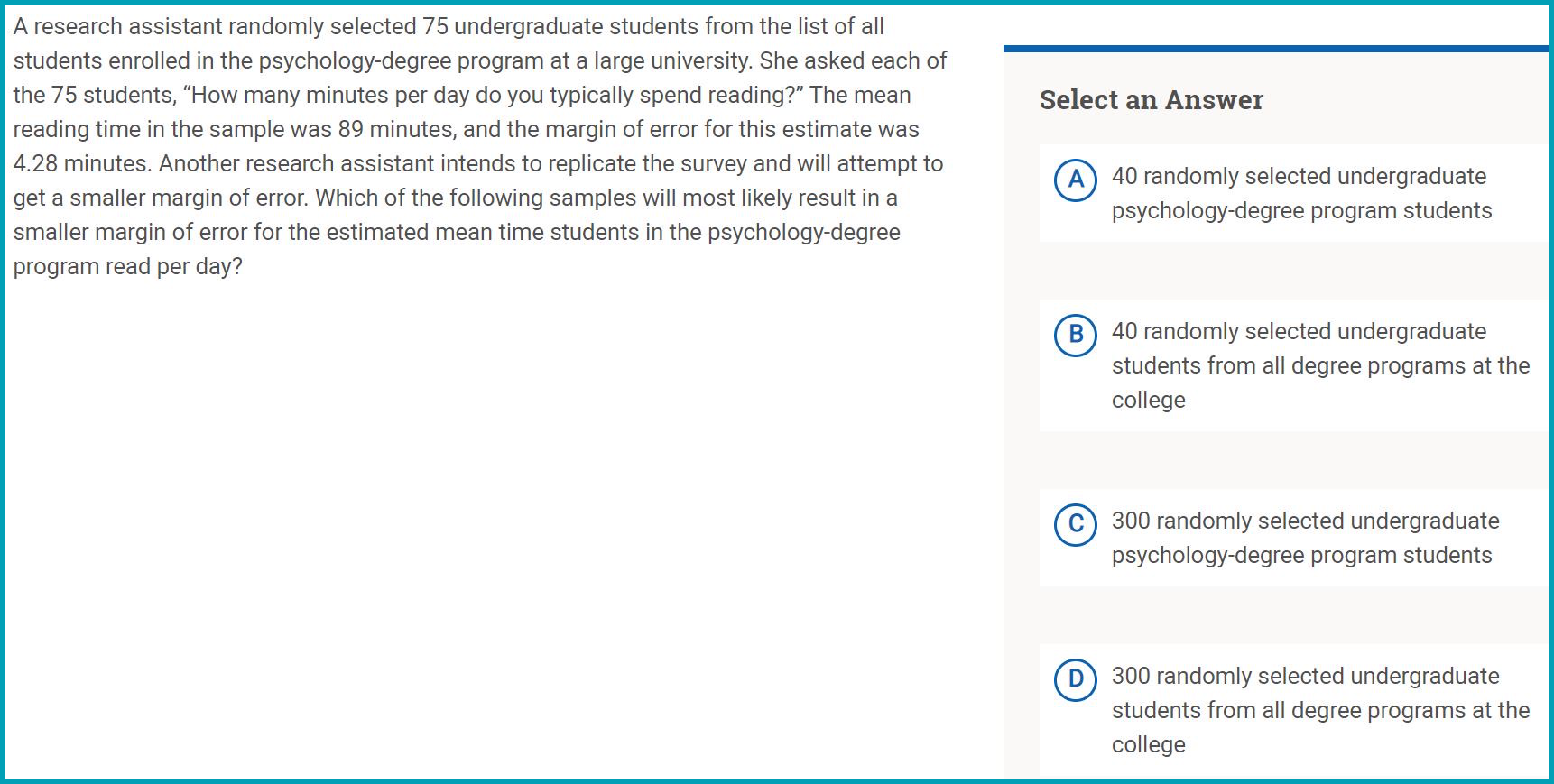
Measures of spread and center

Calculate mean, median, mode, and range based on sample data provided (lists of values, tables, dot plots, bar graphs, histograms, etc.). Know about standard deviation (won’t be asked to calculate it though).

Data collection methods

Evaluate whether the method of data collection is appropriate given the context of the problem.

Passport to Advanced Math (14 questions)

Write quadratic/ exponential models given the context

Convert equations to different forms depending on what the problem asks (like changing from quadratic to vertex form)

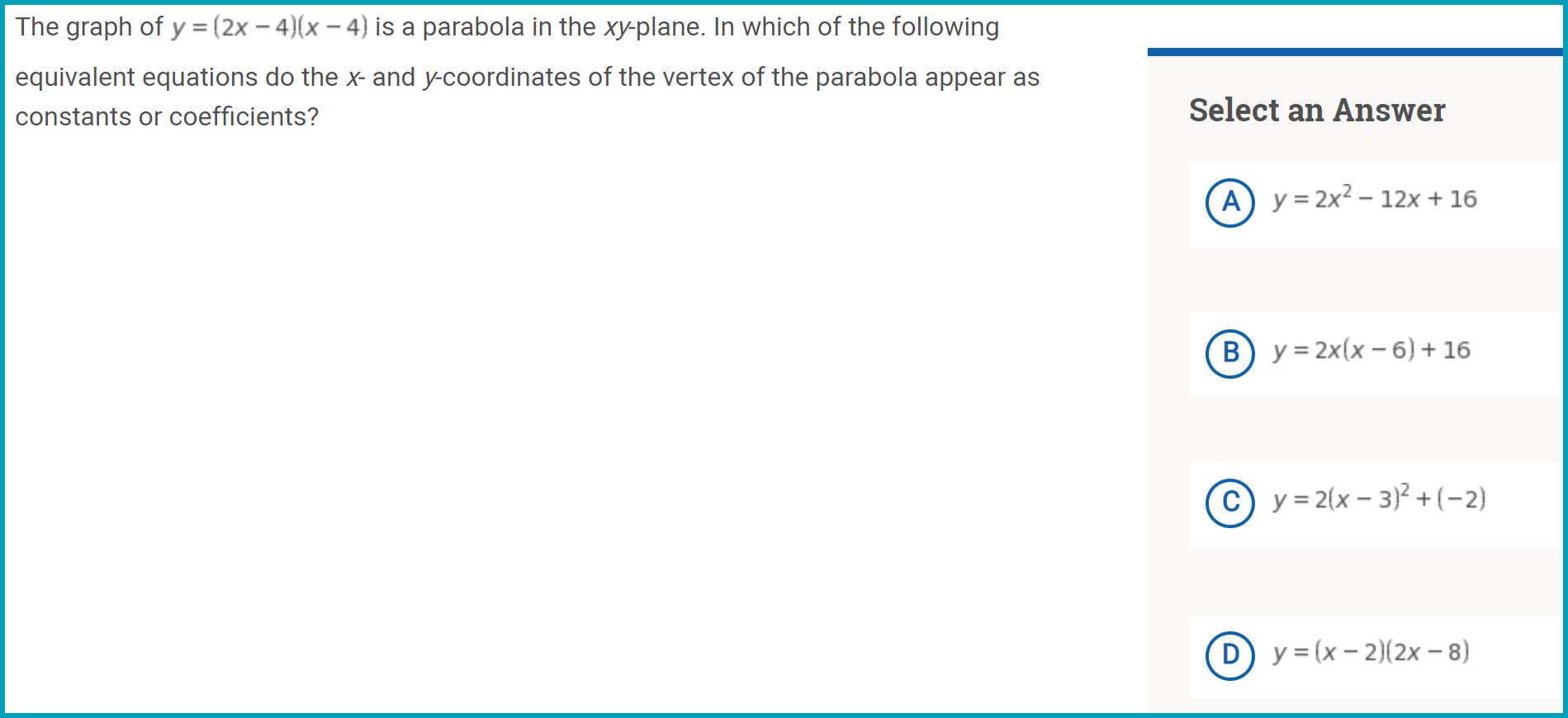
Writing expressions with rational exponents and radicals

Writing an algebraic expression in an equivalent form

Solve quadratic equations

Use quadratic formula if written in standard form. Otherwise, in factored form, the zeroes are just found by making each part equal to zero. If written in standard form, you would have to find the max/min first, and then determine the zeroes.

Add/subtract/multiply polynomial expressions

It won't just be one operation though. There are often multiple steps involved.

Solve equation with a variable with a radical or in the denominator

Solve a 2 equation system with 1 linear equation and 1 quadratic equation

Simplify/rewrite rational expressions

Also understand the domain and range of a rational function. Know how to find zeroes and when the function is undefined.

Relate real-life context to parts of nonlinear equation

Nonlinear relationship between two variables

Given a nonlinear equation, select a graph (and vice versa), relating graphs to solving systems of equations, equation of curve given verbal information of graph, evaluate how changes in the equation result in changes in the corresponding graph, and find components of linear equation from its equation.

Solving problems using function notation and transformations on these functions.

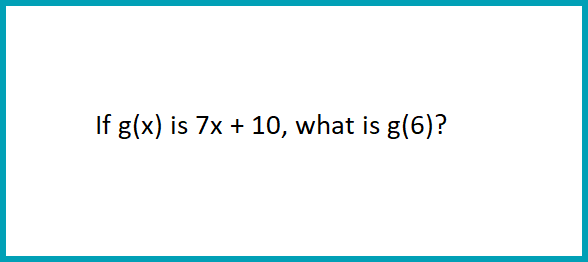
Rearranging an equation to find determine desired variable

This is usually when the question wants the variable to be in terms of another variable. For example, s = 3/2b + 7.

Additional topics (2 questions)

Problems using volume formulas

We can finally use the formula sheet! You are not always looking for the volume though. For example, you may be asked to find the radius or height given the volume and other context.

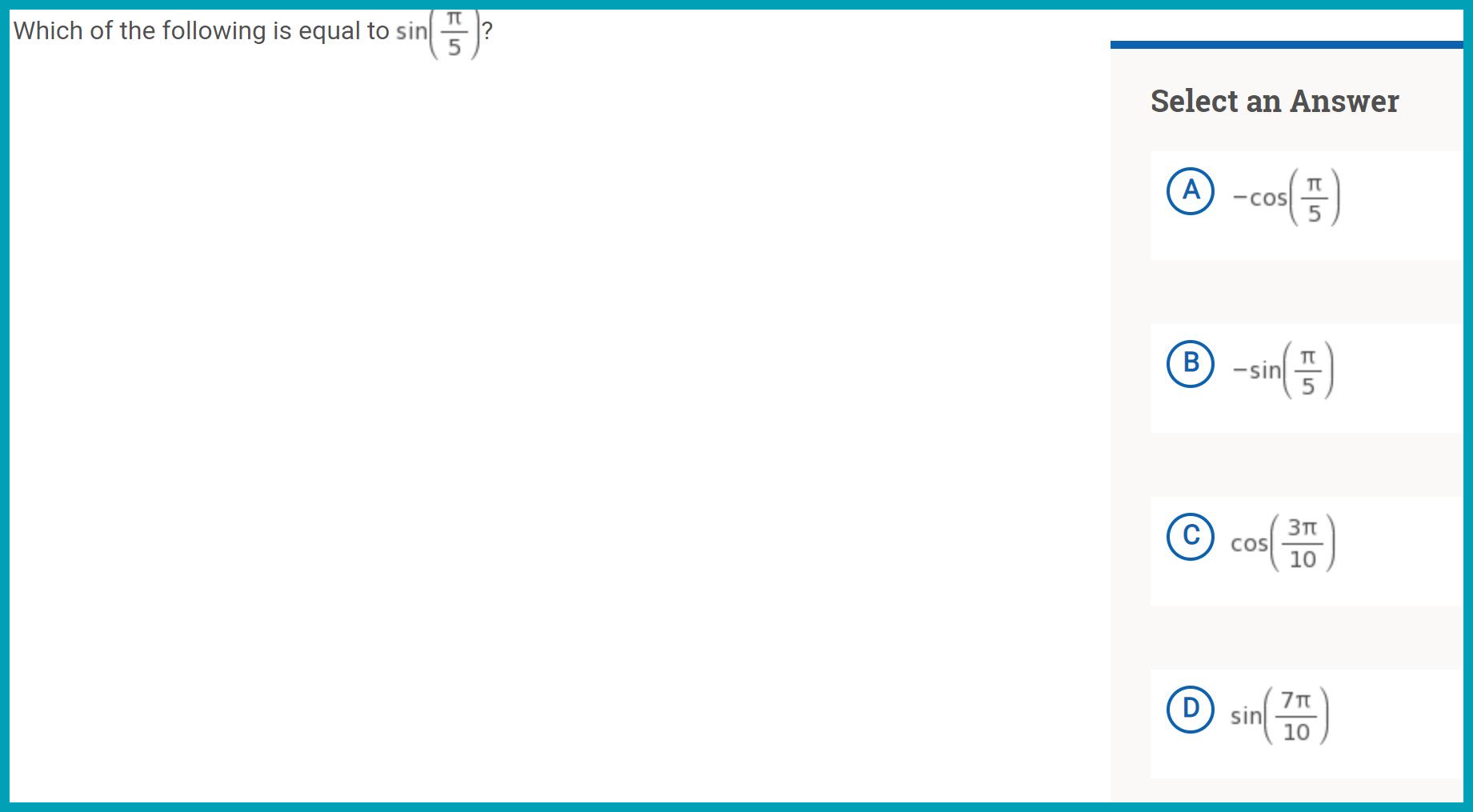
Trigonometric ratios and Pythagorean theorem

Degree/radian conversion, arc length calculations, trigonometric function calculations (using radians)

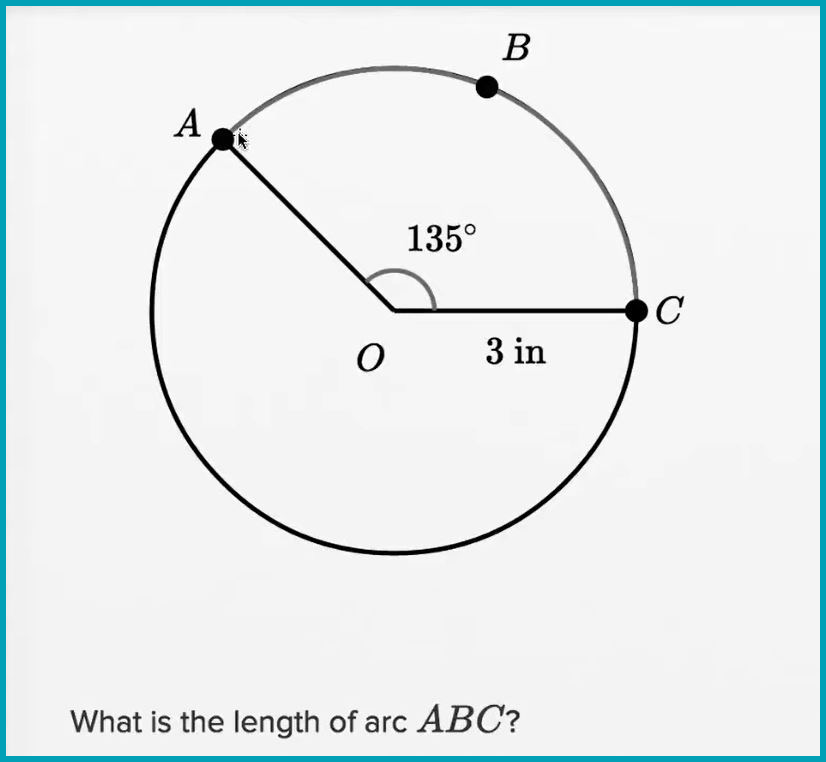
Calculate radius, diameter, chord length, angle, arc, and sector area using information given about circles and lines.

‍

Triangle congruence/similarity theorems and intersecting lines theorems

These theorems are used to find missing lengths, angle measures in triangles. In reverse, these values can be given to prove a theorem.

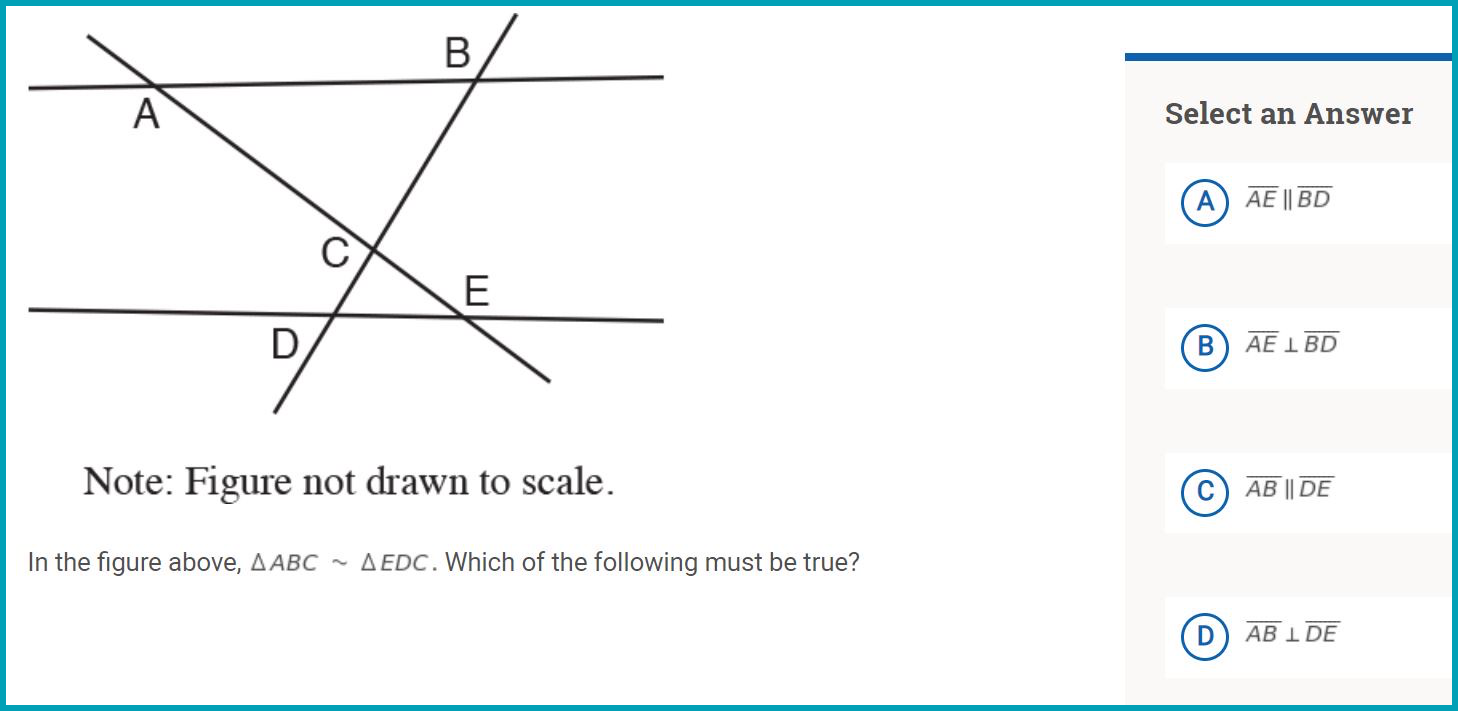
Right triangles relating to similarity, trig ratios, and sine and cosine of complementary angles

These relationships used to find missing lengths, angle measures in triangles. In reverse, these values can be given to prove a theorem.

Graphing and writing an equation of a circle

Also understand the properties of a circle (ex. The radius; translating left, right, up, and down; center point).

More resources to practice

Khan Academy — Though they don’t have official PSAT material, they have amazing resources for the SAT providing guidance on the common types of problems seen on the SAT. PSAT math is essentially similar to the SAT math. Like they say, math is math.

CrackSAT — They provide plenty of practice tests to fully prepare you for big test day! The best way to get better at anything is to practice!

Varsity Tutors — They provide plenty of PSAT practice tests along with 10 diagnostic tests.

✏️ Make sure to check out the Fiveable guides for Reading and Writing!

REMEMBER that there are numerous resources found online; there is no necessity to buy expensive PSAT prep books.

Good luck on your future PSAT! 😀