
Unit 1 Overview: Limits and Continuity
9 min read•february 15, 2024
Kashvi Panjolia
Kashvi Panjolia
Introduction to Calculus
In this unit, you’ll learn about the essential basics of calculus. Limits and continuity are the backgrounds for all of AP Calculus so it's crucial to understand these concepts. This unit makes up about 10-12% of the AP Calculus AB Exam or 4-7% of the AP Calculus BC Exam.
Calculus is a branch of mathematics that deals with the study of change and motion. One of the main questions that calculus aims to answer is "Can change occur at an instant?"
This question refers to the idea that change is not always a gradual process, but can occur suddenly and at a specific moment in time. To better understand this concept, let's consider the example of a moving arrow.
Imagine an arrow that is moving across a screen. At a particular moment in time, the arrow's position on the screen changes. If we were to take a series of snapshots of the arrow's position at different points in time, we would see that the arrow is moving and its position is changing over time. However, when we look at a single snapshot, it appears that the arrow's position has changed instantaneously.
This is an example of how change can occur at an instant. Even though the arrow's motion is a continuous process, at a specific moment in time, its position changes abruptly. To further understand this question, we first need to understand the concept of a limit.
1.1 Introducing Calculus: Can Change Occur at an Instant?
There are two different types of rates in calculus: average rate of change (AROC) and instantaneous rate of change (IROC). The average rate of change is the slope of the secant line between two points of a function. The formula for the average rate of change is:
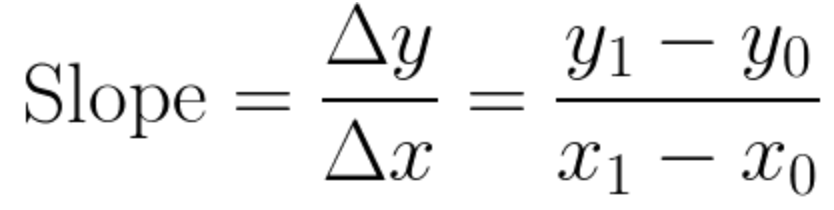
Image courtesy of Medium.
Recall from your algebra class that this is simply the formula for the slope of a straight line. It is important to note that if the denominator of this formula evaluates to zero, the average rate of change will be undefined since division by zero is not possible.
1.2 Defining Limits and Using Limit Notation
A limit is a value that a function approaches as the input (or independent variable) gets closer to a certain value. Limits are used to understand the instantaneous rate of change. For example, as x approaches 2, the value of the function f(x) = x^2 approaches 4. This means that the limit of f(x) as x approaches 2 is 4.
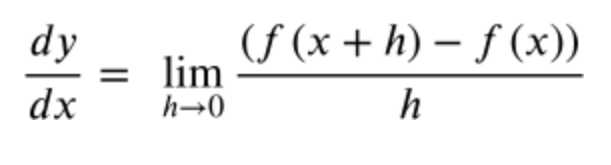
The mathematical definition of a limit, shown below, is important to understand as this definition will help us understand derivatives in a later unit.
To read limit notation, you want to start by looking at the "a" value along the x-axis of the function f(x). Once you reach the "a" value along the x-axis, you want to evaluate the limit by finding the y value of the function.
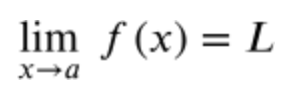
This notation is read as "the limit of f(x) as x approaches a is L." In the remaining guides, we will explore different ways to solve limits.
1.3 Estimating from Graphs
Estimating the limit of a function from its graph involves analyzing the behavior of the function as the independent variable approaches a certain value. There are two types of limits: one-sided limits and two-sided limits. A one-sided limit is the limit of a function as the independent variable approaches a certain value from one direction. For example, the limit of a function as x approaches 2 from the left is different than the limit of the same function as x approaches 2 from the right.
A two-sided limit is the limit of a function as the independent variable approaches a certain value from both directions. For example, the limit of a function as x approaches 2 from both the left and the right is the same. If the function appears to approach a specific value as the independent variable approaches the value in question, then the limit exists and we can estimate its value by looking at the function's graph.
However, a limit may not exist in certain cases. For example, if a function oscillates or becomes unbounded as the independent variable approaches a certain value, the limit does not exist. Additionally, if the function has a vertical asymptote, the limit does not exist.
1.4 Estimating from Tables
When estimating the limit from a table, you want to get as close to the x value as possible from both sides of the function. In this case, as x approaches two from the left (the lower numbers), the function approaches -1000, but as x approaches 2 from the right, the function approaches 1000. Since the limits from the left and right are not equal, the limit as x approaches 2 does not exist.
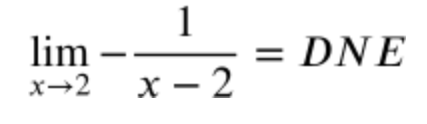
| x | 1.9 | 1.99 | 1.999 | 2 | 2.001 | 2.01 | 2.1 |
| f(x) | -10 | -100 | -1000 | ? | 1000 | 100 | 10 |
1.5 Using Algebraic Properties of Limits
The limit properties below will help us understand how to evaluate limits. These properties are very straightforward but important to understand nonetheless.
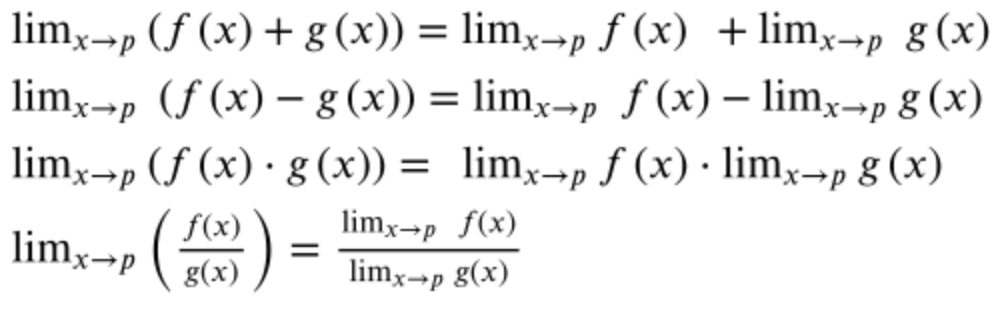
1.6 Using Algebraic Manipulations
There are a few different ways to solve limits algebraically. The four that are typically used in Calculus are substitution, factoring, common denominator, and conjugate.
Substitution: This method involves replacing the independent variable with the value at which we want to find the limit. For example, if we want to find the limit of f(x) = x^2 as x approaches 2, we can replace x with 2 and find that the limit is 4.
Factoring: This method involves factoring the numerator and denominator of the function if possible. For example, if we have the limit of (x^2-4)/(x-2) as x approaches 2, we can factor the numerator to get (x+2)(x-2) and find that the limit does not exist. Even though we are left with (x+2) after canceling out the common factors, if we look back at our original function we can see that substituting 2 for x in the expression (x-2) would cause the denominator of the factor to be zero, making the limited undefined.
Creating a common denominator: This method involves multiplying both the numerator and denominator of the function by a common denominator if they have different denominators. For example, if we have the limit of (x^2+3x)/(x+2) - (2x-1)/(x+2) as x approaches -2, we can create a common denominator of (x+2) and find that the limit is -1/4.
Multiplying by the conjugate: This method involves multiplying the numerator and denominator of a fraction by the conjugate of the denominator. The conjugate of a binomial is the binomial with the opposite sign between the terms. This method is particularly useful when the denominator has a root that makes the fraction indeterminate. For example, if we have the limit of (x-2)/(x^2-4) as x approaches 2, we can multiply the numerator and denominator by x+2, the conjugate of x-2, to find that the limit is 1.
1.8 Squeeze Theorem
This theorem can also be called the sandwich or pinching theorem. The squeeze theorem is used to solve the limit of a function by comparing it to two other functions whose limits are known or easier to compute. The basic idea behind the squeeze theorem is that if we have two functions, f(x) and g(x), where f(x)<g(x)<h(x) for all x in a certain interval except possibly at x=a, and if we know the limit of f(x) and h(x) as x approaches a, then the limit of g(x) as x approaches a must be between the limits of f(x) and h(x).
1.10 Exploring Types of Discontinuities
Jump Discontinuity: Typically this type of discontinuity is seen in a piecewise function.
Removable Discontinuity: When the function seems to be continuous but there is a hole on the function itself, meaning the actual y value exists or doesn’t exist elsewhere on the graph.
Infinite Discontinuity: This is a function that has an asymptote somewhere on the function.
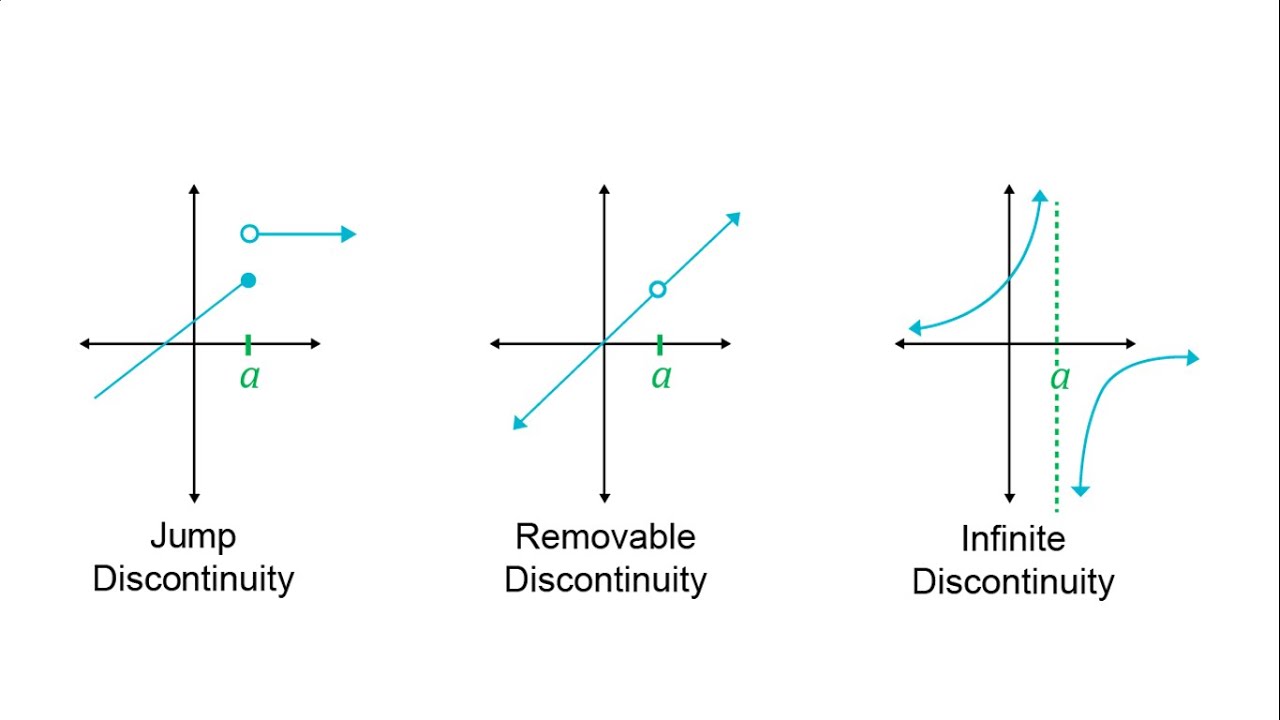
Image courtesy of Matlab and Maths Tutorials.
1.11 Defining Continuity at a Point
There are three different requirements to prove continuity. Remember that a continuous function is one that you can draw without picking up your pencil.
The first requirement is that f(a) at x=a is defined. This means that there should be a real y-value on the function for the value a. The second requirement, shown below, is that the limit of f(a) as x approaches a exists. This can be checked by making sure there are no discontinuities and by ensuring the limit as x approaches a from the left is equal to the limit as x approaches a from the right. The third requirement is that the limit of f(a) as x approaches a should be equal to the function value (y) at x=a.
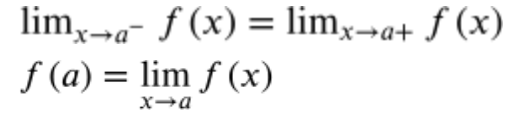
1.12 Confirming Continuity Over an Interval
A function is considered continuous over an interval if it satisfies the following three conditions:
- The function is defined at every point within the interval.
- The function has no jumps, breaks, or holes within the interval.
- The limit of the function as the independent variable approaches any point within the interval equals the function's value at that point.
There are certain types of functions that are continuous on all points in their domain. These include, but are not limited to:
Polynomial functions: These functions are continuous over their entire domain, which is the set of all real numbers.
Rational functions: These are functions of the form f(x) = (p(x))/(q(x)), where p(x) and q(x) are polynomials. These functions are continuous over their entire domain, which is the set of all real numbers except for the values of x that make the denominator equal to zero.
Trigonometric functions: These are functions such as sin(x), cos(x), tan(x), etc. These functions are continuous over their entire domain, which is the set of all real numbers.
Exponential functions: The function e^x is continuous over its entire domain, which is the set of all real numbers.
It's important to note that there are also functions that are not continuous on all points in their domain; for example, the absolute value function is not continuous at x=0, or the function 1/x is not continuous at x=0.
1.13 Removing Discontinuities
When the limit of a function exists at a point where the function is discontinuous, it is possible to remove the discontinuity by redefining the value of the function at that point to match the value of the limit. If the limit of the function exists at a point where the function is discontinuous, it means that the two limits from the left and right are equal, so we just need to redefine the value of the function for that one point. We can do this by creating a piecewise function.
Oscillating Function: This function will forever oscillate between multiple numbers. These functions are typically periodic functions.
1.14 & 1.15 Asymptotes
Vertical asymptotes can be found by setting the denominator of the rational expression equal to zero. When the denominator is zero, there exists a vertical asymptote because it is not possible to divide by zero for that specific point.
Horizontal asymptotes can be found by looking at the degree of the rational expression. If the degree in the numerator and denominator is the same, the horizontal asymptote is at the coefficient of the top degree divided by the coefficient of the bottom degree. If the degree is larger in the numerator, the rational expression has a slant asymptote. If the degree in the denominator is larger the horizontal asymptote will be at y=0.
1.16 Working with the Intermediate Value Theorem (IVT)
The Intermediate Value Theorem (IVT) is a fundamental theorem in calculus that states that for any continuous function f(x) over a closed interval [a,b], and for any value c between f(a) and f(b), there exists at least one value x in the interval [a,b] such that f(x) = c.
In simpler terms, the Intermediate Value Theorem states that if a continuous function takes on two different values at two different points within an interval, then it must take on all values between those two points somewhere within the interval.
For example, if we have a function f(x) = x^2, and we know that f(-1) = 1 and f(1) = 1, we can say that there must be a value x between -1 and 1 such that f(x) = 0, because the function is continuous, so it must take on all values between 1 and 1 somewhere within the interval [-1,1].
It's important to note that for the Intermediate Value Theorem to hold, the function must be continuous over the interval in question. If the function has a jump, break or hole, the theorem does not apply.

Image courtesy of Quizlet.
Unit 1 Overview: Limits and Continuity
9 min read•february 15, 2024
Kashvi Panjolia
Kashvi Panjolia
Introduction to Calculus
In this unit, you’ll learn about the essential basics of calculus. Limits and continuity are the backgrounds for all of AP Calculus so it's crucial to understand these concepts. This unit makes up about 10-12% of the AP Calculus AB Exam or 4-7% of the AP Calculus BC Exam.
Calculus is a branch of mathematics that deals with the study of change and motion. One of the main questions that calculus aims to answer is "Can change occur at an instant?"
This question refers to the idea that change is not always a gradual process, but can occur suddenly and at a specific moment in time. To better understand this concept, let's consider the example of a moving arrow.
Imagine an arrow that is moving across a screen. At a particular moment in time, the arrow's position on the screen changes. If we were to take a series of snapshots of the arrow's position at different points in time, we would see that the arrow is moving and its position is changing over time. However, when we look at a single snapshot, it appears that the arrow's position has changed instantaneously.
This is an example of how change can occur at an instant. Even though the arrow's motion is a continuous process, at a specific moment in time, its position changes abruptly. To further understand this question, we first need to understand the concept of a limit.
1.1 Introducing Calculus: Can Change Occur at an Instant?
There are two different types of rates in calculus: average rate of change (AROC) and instantaneous rate of change (IROC). The average rate of change is the slope of the secant line between two points of a function. The formula for the average rate of change is:
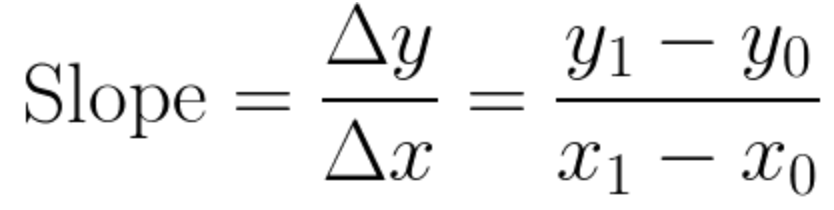
Image courtesy of Medium.
Recall from your algebra class that this is simply the formula for the slope of a straight line. It is important to note that if the denominator of this formula evaluates to zero, the average rate of change will be undefined since division by zero is not possible.
1.2 Defining Limits and Using Limit Notation
A limit is a value that a function approaches as the input (or independent variable) gets closer to a certain value. Limits are used to understand the instantaneous rate of change. For example, as x approaches 2, the value of the function f(x) = x^2 approaches 4. This means that the limit of f(x) as x approaches 2 is 4.
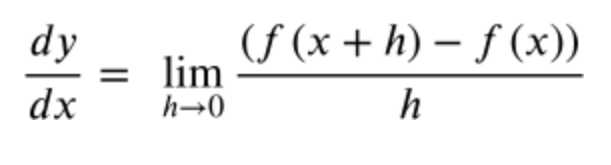
The mathematical definition of a limit, shown below, is important to understand as this definition will help us understand derivatives in a later unit.
To read limit notation, you want to start by looking at the "a" value along the x-axis of the function f(x). Once you reach the "a" value along the x-axis, you want to evaluate the limit by finding the y value of the function.
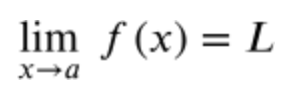
This notation is read as "the limit of f(x) as x approaches a is L." In the remaining guides, we will explore different ways to solve limits.
1.3 Estimating from Graphs
Estimating the limit of a function from its graph involves analyzing the behavior of the function as the independent variable approaches a certain value. There are two types of limits: one-sided limits and two-sided limits. A one-sided limit is the limit of a function as the independent variable approaches a certain value from one direction. For example, the limit of a function as x approaches 2 from the left is different than the limit of the same function as x approaches 2 from the right.
A two-sided limit is the limit of a function as the independent variable approaches a certain value from both directions. For example, the limit of a function as x approaches 2 from both the left and the right is the same. If the function appears to approach a specific value as the independent variable approaches the value in question, then the limit exists and we can estimate its value by looking at the function's graph.
However, a limit may not exist in certain cases. For example, if a function oscillates or becomes unbounded as the independent variable approaches a certain value, the limit does not exist. Additionally, if the function has a vertical asymptote, the limit does not exist.
1.4 Estimating from Tables
When estimating the limit from a table, you want to get as close to the x value as possible from both sides of the function. In this case, as x approaches two from the left (the lower numbers), the function approaches -1000, but as x approaches 2 from the right, the function approaches 1000. Since the limits from the left and right are not equal, the limit as x approaches 2 does not exist.
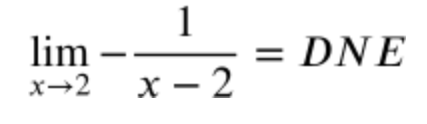
| x | 1.9 | 1.99 | 1.999 | 2 | 2.001 | 2.01 | 2.1 |
| f(x) | -10 | -100 | -1000 | ? | 1000 | 100 | 10 |
1.5 Using Algebraic Properties of Limits
The limit properties below will help us understand how to evaluate limits. These properties are very straightforward but important to understand nonetheless.
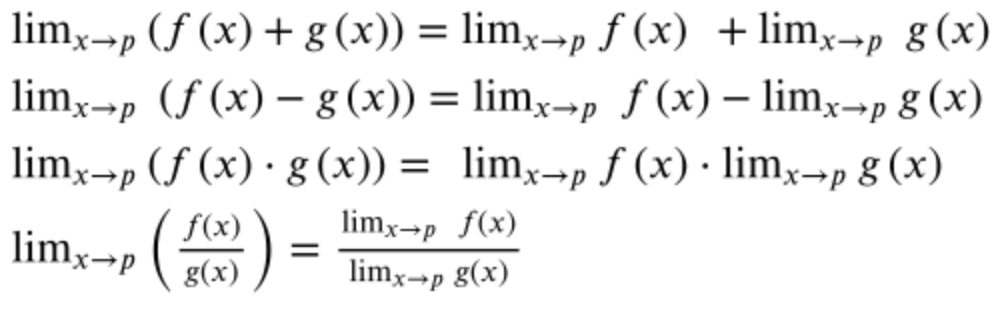
1.6 Using Algebraic Manipulations
There are a few different ways to solve limits algebraically. The four that are typically used in Calculus are substitution, factoring, common denominator, and conjugate.
Substitution: This method involves replacing the independent variable with the value at which we want to find the limit. For example, if we want to find the limit of f(x) = x^2 as x approaches 2, we can replace x with 2 and find that the limit is 4.
Factoring: This method involves factoring the numerator and denominator of the function if possible. For example, if we have the limit of (x^2-4)/(x-2) as x approaches 2, we can factor the numerator to get (x+2)(x-2) and find that the limit does not exist. Even though we are left with (x+2) after canceling out the common factors, if we look back at our original function we can see that substituting 2 for x in the expression (x-2) would cause the denominator of the factor to be zero, making the limited undefined.
Creating a common denominator: This method involves multiplying both the numerator and denominator of the function by a common denominator if they have different denominators. For example, if we have the limit of (x^2+3x)/(x+2) - (2x-1)/(x+2) as x approaches -2, we can create a common denominator of (x+2) and find that the limit is -1/4.
Multiplying by the conjugate: This method involves multiplying the numerator and denominator of a fraction by the conjugate of the denominator. The conjugate of a binomial is the binomial with the opposite sign between the terms. This method is particularly useful when the denominator has a root that makes the fraction indeterminate. For example, if we have the limit of (x-2)/(x^2-4) as x approaches 2, we can multiply the numerator and denominator by x+2, the conjugate of x-2, to find that the limit is 1.
1.8 Squeeze Theorem
This theorem can also be called the sandwich or pinching theorem. The squeeze theorem is used to solve the limit of a function by comparing it to two other functions whose limits are known or easier to compute. The basic idea behind the squeeze theorem is that if we have two functions, f(x) and g(x), where f(x)<g(x)<h(x) for all x in a certain interval except possibly at x=a, and if we know the limit of f(x) and h(x) as x approaches a, then the limit of g(x) as x approaches a must be between the limits of f(x) and h(x).

1.10 Exploring Types of Discontinuities
Jump Discontinuity: Typically this type of discontinuity is seen in a piecewise function.
Removable Discontinuity: When the function seems to be continuous but there is a hole on the function itself, meaning the actual y value exists or doesn’t exist elsewhere on the graph.
Infinite Discontinuity: This is a function that has an asymptote somewhere on the function.

Image courtesy of Matlab and Maths Tutorials.
1.11 Defining Continuity at a Point
There are three different requirements to prove continuity. Remember that a continuous function is one that you can draw without picking up your pencil.
The first requirement is that f(a) at x=a is defined. This means that there should be a real y-value on the function for the value a. The second requirement, shown below, is that the limit of f(a) as x approaches a exists. This can be checked by making sure there are no discontinuities and by ensuring the limit as x approaches a from the left is equal to the limit as x approaches a from the right. The third requirement is that the limit of f(a) as x approaches a should be equal to the function value (y) at x=a.
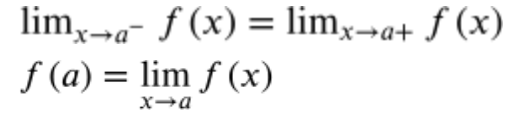
1.12 Confirming Continuity Over an Interval
A function is considered continuous over an interval if it satisfies the following three conditions:
- The function is defined at every point within the interval.
- The function has no jumps, breaks, or holes within the interval.
- The limit of the function as the independent variable approaches any point within the interval equals the function's value at that point.
There are certain types of functions that are continuous on all points in their domain. These include, but are not limited to:
Polynomial functions: These functions are continuous over their entire domain, which is the set of all real numbers.
Rational functions: These are functions of the form f(x) = (p(x))/(q(x)), where p(x) and q(x) are polynomials. These functions are continuous over their entire domain, which is the set of all real numbers except for the values of x that make the denominator equal to zero.
Trigonometric functions: These are functions such as sin(x), cos(x), tan(x), etc. These functions are continuous over their entire domain, which is the set of all real numbers.
Exponential functions: The function e^x is continuous over its entire domain, which is the set of all real numbers.
It's important to note that there are also functions that are not continuous on all points in their domain; for example, the absolute value function is not continuous at x=0, or the function 1/x is not continuous at x=0.
1.13 Removing Discontinuities
When the limit of a function exists at a point where the function is discontinuous, it is possible to remove the discontinuity by redefining the value of the function at that point to match the value of the limit. If the limit of the function exists at a point where the function is discontinuous, it means that the two limits from the left and right are equal, so we just need to redefine the value of the function for that one point. We can do this by creating a piecewise function.
Oscillating Function: This function will forever oscillate between multiple numbers. These functions are typically periodic functions.
1.14 & 1.15 Asymptotes
Vertical asymptotes can be found by setting the denominator of the rational expression equal to zero. When the denominator is zero, there exists a vertical asymptote because it is not possible to divide by zero for that specific point.
Horizontal asymptotes can be found by looking at the degree of the rational expression. If the degree in the numerator and denominator is the same, the horizontal asymptote is at the coefficient of the top degree divided by the coefficient of the bottom degree. If the degree is larger in the numerator, the rational expression has a slant asymptote. If the degree in the denominator is larger the horizontal asymptote will be at y=0.
1.16 Working with the Intermediate Value Theorem (IVT)
The Intermediate Value Theorem (IVT) is a fundamental theorem in calculus that states that for any continuous function f(x) over a closed interval [a,b], and for any value c between f(a) and f(b), there exists at least one value x in the interval [a,b] such that f(x) = c.
In simpler terms, the Intermediate Value Theorem states that if a continuous function takes on two different values at two different points within an interval, then it must take on all values between those two points somewhere within the interval.
For example, if we have a function f(x) = x^2, and we know that f(-1) = 1 and f(1) = 1, we can say that there must be a value x between -1 and 1 such that f(x) = 0, because the function is continuous, so it must take on all values between 1 and 1 somewhere within the interval [-1,1].
It's important to note that for the Intermediate Value Theorem to hold, the function must be continuous over the interval in question. If the function has a jump, break or hole, the theorem does not apply.

Image courtesy of Quizlet.

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.