Glossary

10.5 Constraint optimization problems

10 min read•august 21, 2024

is a powerful tool in , focusing on finding the best solutions within defined limits. It combines math modeling, algorithms, and problem-solving to tackle complex real-world challenges in various fields.

This topic covers the fundamentals, , solution methods, and applications of constraint optimization. It explores key concepts like variables, , and objective functions, as well as techniques for solving these problems efficiently.

Fundamentals of constraint optimization

  • Constraint optimization forms a crucial subset of combinatorial optimization focusing on finding optimal solutions within defined constraints
  • Combines elements of mathematical modeling, algorithmic design, and problem-solving techniques to address complex real-world optimization challenges
  • Serves as a foundation for tackling various optimization problems in fields such as operations research, artificial intelligence, and computer science

Definition and components

Top images from around the web for Definition and components

  • Finding the optimal Bayesian network given a constraint graph [PeerJ] View original

    Is this image relevant?

  • A local cost simulation-based algorithm to solve distributed constraint optimization problems ... View original

    Is this image relevant?

  • Finding the optimal Bayesian network given a constraint graph [PeerJ] View original

    Is this image relevant?

1 of 3

Top images from around the web for Definition and components

  • Finding the optimal Bayesian network given a constraint graph [PeerJ] View original

    Is this image relevant?

  • A local cost simulation-based algorithm to solve distributed constraint optimization problems ... View original

    Is this image relevant?

  • Finding the optimal Bayesian network given a constraint graph [PeerJ] View original

    Is this image relevant?

1 of 3
  • Mathematical framework for finding the best solution from a set of feasible alternatives
  • represent the quantities to be determined in the optimization process
  • Constraints define the limitations or requirements that the solution must satisfy
  • quantifies the quality of a solution, typically minimized or maximized
  • encompasses all possible combinations of decision variable values

Types of constraints

  • must be satisfied for a solution to be considered feasible
  • can be violated but incur penalties in the objective function
  • require specific values or relationships between variables
  • define upper or lower bounds on variables or expressions
  • involve complex relationships among multiple variables (all-different constraint)

Objective function characteristics

  • consist of a weighted sum of decision variables
  • involve more complex relationships between variables
  • guarantee a global optimum can be found efficiently
  • may have multiple local optima, making global optimization challenging
  • balance multiple, often conflicting, optimization goals

Problem formulation techniques

  • Problem formulation serves as a critical step in the constraint optimization process, bridging real-world problems and mathematical models
  • Effective formulation techniques enable the application of powerful optimization algorithms and solvers to complex practical problems
  • Proper problem formulation often determines the success and efficiency of the subsequent optimization process

Variable identification

  • Determine the key decisions or quantities to be optimized in the problem
  • represent quantities that can take any real value within a range
  • are restricted to whole number values, often used for discrete decisions
  • represent yes/no decisions or on/off states
  • introduced to simplify complex constraints or objective functions

Constraint representation

  • Express problem limitations and requirements as mathematical equations or inequalities
  • capture if-then relationships or conditional requirements
  • limit the usage of available resources (time, money, materials)
  • define ordering relationships between activities or events
  • ensure equilibrium or conservation in system components

Objective function construction

  • Identify the primary goal or metric to be optimized (cost, profit, time, efficiency)
  • Incorporate relevant decision variables and their coefficients or relationships
  • Consider trade-offs between multiple objectives if applicable
  • Normalize different units or scales to ensure proper weighting of components
  • Validate the objective function against expected behavior and known optimal solutions

Solution methods

  • Solution methods in constraint optimization encompass a wide range of algorithms and techniques for finding optimal or near-optimal solutions
  • The choice of solution method depends on the problem structure, size, and desired solution quality
  • Effective solution methods balance computational efficiency with solution quality to address practical optimization challenges

Complete vs heuristic approaches

  • Complete methods guarantee finding the optimal solution if one exists
  • algorithm systematically explores the solution space, pruning suboptimal branches
  • breaks down complex problems into simpler subproblems
  • trade optimality for computational efficiency
  • make locally optimal choices at each step
  • (genetic algorithms, ) explore large solution spaces effectively

Local search algorithms

  • Start with an initial solution and iteratively improve it by exploring neighboring solutions
  • moves to the best neighboring solution until no improvement is possible
  • maintains a list of recently visited solutions to avoid cycling
  • Simulated annealing allows occasional moves to worse solutions to escape local optima
  • systematically changes the neighborhood structure

Constraint propagation techniques

  • Reduce the search space by inferring additional constraints from existing ones
  • eliminates inconsistent values from future variables
  • ensures consistency between pairs of variables
  • extends arc consistency to non-binary constraints
  • maintains consistency on the upper and lower bounds of variables

Constraint satisfaction problems

  • form a fundamental class of problems in constraint optimization
  • CSPs focus on finding assignments to variables that satisfy a set of constraints without necessarily optimizing an objective function
  • Many real-world problems can be naturally formulated as CSPs, making them a crucial area of study in combinatorial optimization

Relation to constraint optimization

  • CSPs can be viewed as a special case of constraint optimization with a binary objective function
  • Many constraint optimization techniques originated from or build upon CSP solving methods
  • CSP solving often serves as a subproblem in more complex constraint optimization problems
  • Feasibility in constraint optimization corresponds to finding a solution in CSPs
  • Optimization can be achieved by iteratively solving CSPs with tightening bounds

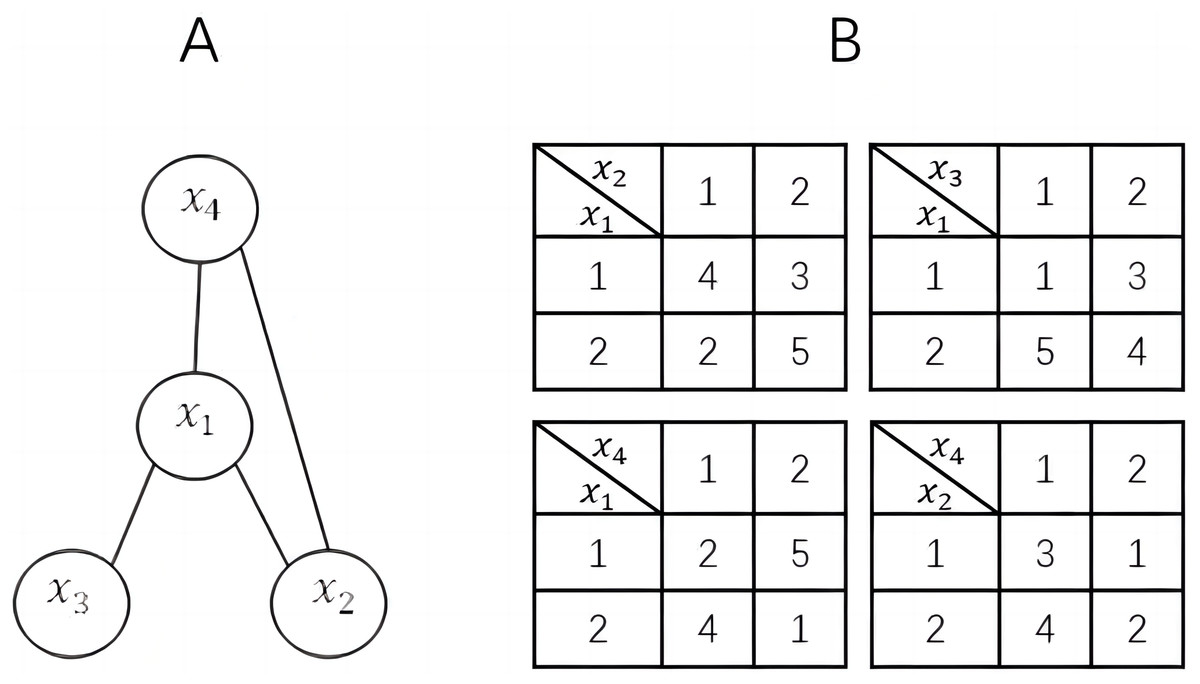
Arc consistency

  • Ensures that every value in a variable's domain is consistent with the binary constraints
  • efficiently achieves arc consistency through constraint propagation
  • Reduces the search space by eliminating inconsistent values from variable domains
  • Serves as a preprocessing step or can be interleaved with search algorithms
  • Generalized to higher-order constraints through algorithms like GAC-Schema
  • Systematic search algorithm for solving CSPs by assigning values to variables one at a time
  • returns to the most recently assigned variable when a dead-end is reached
  • combines backtracking with constraint propagation to detect failures early
  • identifies the source of conflicts to make larger backtracking steps
  • Heuristics like and improve search efficiency

Linear programming in constraints

  • represents a powerful optimization technique widely used in constraint optimization
  • LP problems involve optimizing a linear objective function subject to linear constraints
  • Many combinatorial optimization problems can be formulated as or approximated by linear programs

Standard form

  • Expresses LP problems in a canonical form for solving with standard algorithms
  • Objective function is always minimization (maximization problems can be converted)
  • All constraints are expressed as equalities using slack or surplus variables
  • All variables are non-negative
  • Matrix notation min⁡cTx subject to Ax=b,x≥0\min c^T x \text{ subject to } Ax = b, x \geq 0 concisely represents the problem

Simplex method

  • Efficient algorithm for solving linear programs developed by George Dantzig
  • Iteratively moves along the vertices of the towards the optimal solution
  • Tableau representation simplifies the computational process
  • Pivoting operations determine the movement from one basic feasible solution to another
  • solves problems where the initial solution is dual feasible but primal infeasible

Integer programming extensions

  • Integer Linear Programming (ILP) restricts some or all variables to integer values
  • Branch and bound algorithm systematically explores integer solutions
  • add constraints to tighten the LP relaxation
  • Branch and cut combines branch and bound with cutting planes for improved efficiency
  • efficiently handles problems with a large number of variables

Applications and case studies

  • Constraint optimization finds widespread applications across various industries and domains
  • Real-world case studies demonstrate the practical impact and challenges of applying constraint optimization techniques
  • Understanding diverse applications helps in recognizing potential optimization opportunities in different fields

Scheduling problems

  • optimizes the allocation of machines to jobs over time
  • assigns crews to flights while minimizing costs and satisfying regulations
  • balances project completion time and resource usage
  • Timetabling for educational institutions assigns courses to time slots and rooms
  • Sports league scheduling creates fair and efficient match schedules

Resource allocation

  • balances risk and return in financial investments
  • determines optimal production and distribution strategies
  • assigns computing resources to tasks or users
  • assigns employees to shifts while meeting demand and preferences
  • Energy dispatch optimizes the allocation of power generation resources

Network design optimization

  • minimizes infrastructure costs while meeting service requirements
  • improves traffic flow and reduces congestion
  • determines optimal locations for facilities and distribution routes
  • enhances performance and reliability
  • identifies key individuals for information dissemination

Constraint optimization software

  • Constraint optimization software provides tools and environments for modeling, solving, and analyzing optimization problems
  • The choice of software depends on the problem complexity, scale, and specific requirements of the application
  • Familiarity with various software options enables practitioners to select the most appropriate tools for their optimization tasks

Commercial solvers

  • CPLEX offers high-performance optimization for linear, mixed-integer, and constraint programming
  • Gurobi provides state-of-the-art solvers for linear, quadratic, and mixed-integer programming
  • FICO Xpress includes modeling tools and solvers for various optimization problems
  • Mathematica integrates symbolic and numeric computation with optimization capabilities
  • AMPL combines a modeling language with interfaces to multiple solvers

Open-source tools

  • provides a suite of optimization tools for various problem types
  • offers a collection of open-source optimization software
  • PuLP allows modeling of linear and integer programming problems in Python
  • OptaPlanner focuses on combinatorial optimization problems with a Java-based framework
  • SCIP (Solving Constraint Integer Programs) combines constraint and integer programming techniques

Modeling languages

  • AMPL (A Mathematical Programming Language) provides a high-level language for describing optimization problems
  • supports various types of mathematical programming problems
  • Pyomo offers Python-based modeling capabilities for optimization problems
  • JuMP provides a domain-specific modeling language for mathematical optimization in Julia
  • MiniZinc combines a high-level modeling language with a wide range of solvers

Advanced topics

  • Advanced topics in constraint optimization push the boundaries of current techniques and methodologies
  • These areas of research address more complex, large-scale, or specialized optimization challenges
  • Understanding advanced topics provides insights into the future directions and potential breakthroughs in the field

Global optimization

  • Focuses on finding the global optimum in non-convex optimization problems
  • Branch and bound techniques for global optimization systematically partition the search space
  • Interval analysis methods use interval arithmetic to bound function values
  • Evolutionary algorithms (genetic algorithms, differential evolution) explore large search spaces
  • Multi-start methods combine local optimization from multiple starting points

Multi-objective constraint optimization

  • Addresses problems with multiple, often conflicting, optimization objectives
  • defines solutions where no objective can be improved without degrading others
  • Weighted sum method combines multiple objectives into a single scalar objective
  • ε-constraint method optimizes one objective while constraining others
  • Multi-objective evolutionary algorithms generate a set of Pareto-optimal solutions

Distributed constraint optimization

  • Deals with optimization problems where variables and constraints are distributed among multiple agents
  • ADOPT (Asynchronous Distributed Optimization) algorithm allows agents to asynchronously choose their variable values
  • DPOP (Distributed Pseudo-tree Optimization Procedure) uses a pseudo-tree structure for efficient message passing
  • performs approximate inference in graphical models for distributed optimization
  • Auction-based methods use economic principles to allocate resources in distributed systems

Performance evaluation

  • Performance evaluation plays a crucial role in assessing and comparing different constraint optimization approaches
  • Proper evaluation techniques help in understanding the strengths and limitations of various algorithms and problem formulations
  • Effective performance evaluation guides the selection and improvement of optimization methods for specific problem domains

Benchmarking techniques

  • Standard problem sets (TSPLib, MIPLib) provide common instances for comparing algorithm performance
  • Random problem generators create diverse instances with controlled properties
  • Cross-validation techniques assess the generalization ability of optimization methods
  • Time-to-target plots compare the time required to reach solutions of a given quality
  • Performance profiles aggregate results across multiple problem instances

Complexity analysis

  • Asymptotic analysis (Big O notation) characterizes the growth rate of computational resources with problem size
  • Worst-case complexity provides upper bounds on resource requirements
  • Average-case complexity analyzes expected performance under typical conditions
  • Parameterized complexity studies how specific problem parameters affect computational difficulty
  • Phase transition analysis identifies regions where problems become particularly hard or easy to solve

Solution quality metrics

  • Optimality gap measures the relative difference between a solution and the known optimal value
  • Approximation ratio bounds the worst-case performance relative to the optimal solution
  • Competitive ratio assesses online algorithms against an omniscient offline algorithm
  • Stability and robustness metrics evaluate solution sensitivity to input perturbations
  • Multi-objective quality indicators (hypervolume, spread) assess Pareto front approximations

Challenges and future directions

  • The field of constraint optimization continues to evolve, addressing new challenges and exploring innovative approaches
  • Understanding current challenges and future directions helps researchers and practitioners anticipate and contribute to advancements in the field
  • Emerging technologies and methodologies offer new opportunities for tackling increasingly complex optimization problems

Scalability issues

  • Handling large-scale optimization problems with millions of variables and constraints
  • Developing efficient decomposition techniques for breaking down complex problems
  • Exploiting problem structure and sparsity for improved computational performance
  • Leveraging parallel and distributed computing architectures for optimization
  • Addressing the curse of dimensionality in high-dimensional optimization problems

Hybrid approaches

  • Combining exact and heuristic methods to balance optimality and computational efficiency
  • Integrating machine learning techniques with traditional optimization algorithms
  • Matheuristics blend mathematical programming and metaheuristics for improved performance
  • Constraint programming and mixed-integer programming hybrids for complex combinatorial problems
  • Hybridizing global and local search methods for effective exploration and exploitation

Quantum computing potential

  • Quantum annealing for solving combinatorial optimization problems
  • Quantum approximate optimization algorithm (QAOA) for near-term quantum devices
  • Developing quantum-inspired classical algorithms for optimization
  • Exploring quantum machine learning approaches for optimization tasks
  • Addressing the challenges of problem embedding and error mitigation in quantum optimization

Key Terms to Review (91)

Ac-3 algorithm: The ac-3 algorithm is a constraint satisfaction algorithm used to reduce the search space in constraint optimization problems by enforcing arc consistency. It works by iteratively examining each arc in a directed graph of variables and constraints, removing values from variable domains that are inconsistent with other connected variables. This process helps in simplifying problems and making it easier to find solutions by ensuring that each value in a variable's domain can be part of some solution.
Airline crew scheduling: Airline crew scheduling is the process of assigning flight crews to flights in a manner that meets regulatory requirements, operational needs, and cost-efficiency. This process involves complex decision-making to ensure that crews are available and qualified for their designated flights while minimizing costs associated with crew wages, layovers, and legal constraints.
AMPL Modeling Language: AMPL (A Mathematical Programming Language) is a high-level programming language designed specifically for formulating and solving mathematical optimization problems, including constraint optimization problems. It allows users to define variables, constraints, and objectives in a clear and concise manner, facilitating the development of complex mathematical models. By using AMPL, users can efficiently express their optimization problems and utilize various solvers to find solutions.
Arc consistency: Arc consistency is a property of a constraint satisfaction problem (CSP) where, for every value of a variable, there exists a consistent value in the connected variable's domain that satisfies the binary constraints between them. This ensures that any assignment of values can potentially lead to a solution, thereby reducing the search space when solving CSPs. Achieving arc consistency is crucial as it helps in eliminating inconsistent values early on, making constraint propagation more efficient and effective in finding solutions to both satisfaction and optimization problems.
Auxiliary Variables: Auxiliary variables are additional variables introduced into a mathematical model to simplify the optimization process or to aid in finding solutions for complex problems. They help in transforming the original problem into a more manageable form, allowing for the application of various optimization techniques and methods. By incorporating auxiliary variables, one can often represent constraints more clearly or break down a problem into smaller, easier-to-solve components.
Balance Constraints: Balance constraints refer to conditions imposed on a mathematical optimization problem that ensure the equilibrium of certain quantities within the system being modeled. These constraints are critical in various applications, such as network flow problems or resource allocation, where maintaining equality between inputs and outputs is essential for achieving optimal solutions. They help define feasible regions and guide the optimization process towards valid and practical outcomes.
Binary variables: Binary variables are decision variables that can take on one of two possible values, typically 0 or 1. These variables are fundamental in various mathematical models and optimization problems, especially where decisions are made in a yes/no or on/off format. They help to represent constraints and objectives in a clear manner, making them essential for formulating and solving problems that involve discrete choices.
Bounds consistency: Bounds consistency is a property of constraint satisfaction problems where the domains of the variables are adjusted to reflect the possible values that satisfy all constraints within the bounds. This means that for any given variable, its bounds are tightened based on the values that can be achieved by other connected variables in the problem. Ensuring bounds consistency helps eliminate infeasible solutions early in the search process, making it particularly important in global constraints and constraint optimization problems.
Branch and Bound: Branch and Bound is an algorithmic technique used to solve optimization problems by systematically exploring branches of a decision tree and using bounds to eliminate suboptimal solutions. This method helps to find the optimal solution more efficiently by avoiding the complete enumeration of all possible solutions, leveraging both exact algorithms and properties of combinatorial structures.
Branch and Cut Method: The branch and cut method is an algorithmic technique used to solve integer programming problems, which involves both branching on variables and cutting planes to tighten the feasible region. This approach combines the strength of branch-and-bound methods with cutting plane techniques, making it effective for tackling complex constraint optimization problems. By systematically exploring feasible solutions and eliminating non-promising regions, this method efficiently finds optimal or near-optimal solutions.
Chronological backtracking: Chronological backtracking is a search strategy used in solving constraint optimization problems, where decisions are made in a specific order and if a constraint is violated, the algorithm backtracks to the previous decision point to explore alternative paths. This technique is particularly useful in finding feasible solutions by systematically exploring and revising the choices made along the way. By maintaining a chronological order of decisions, it helps ensure that potential solutions are evaluated efficiently while adhering to the defined constraints.
Cloud computing resource allocation: Cloud computing resource allocation refers to the process of distributing and managing computing resources such as storage, processing power, and network bandwidth within cloud environments. This ensures optimal use of resources while meeting user demands and maintaining performance levels. Efficient resource allocation is essential for maximizing scalability, minimizing costs, and ensuring that applications run smoothly in a cloud setting.
Coin-or project: The coin-or project is an initiative that focuses on developing and providing open-source software for operations research and optimization, particularly in the realm of mathematical programming. This project has significantly contributed to the field by providing tools and libraries that are freely available for various optimization problems, including linear, integer, and nonlinear programming. It fosters collaboration among researchers and practitioners, aiming to improve accessibility to powerful optimization methods and solutions.
Column generation technique: The column generation technique is a mathematical optimization method used to solve large-scale linear programming problems, particularly in the context of constraint optimization. It works by breaking down a complex problem into smaller subproblems, generating new variables (or columns) as needed to improve the solution. This approach is particularly effective when dealing with problems where the number of possible variables is enormous, allowing for more efficient computations and potentially finding better solutions without needing to consider every variable at once.
Combinatorial optimization: Combinatorial optimization is a branch of mathematical optimization that deals with problems where the objective is to find the best solution from a finite set of discrete options. This field often involves maximizing or minimizing a particular function subject to specific constraints, making it crucial for decision-making in various areas such as logistics, scheduling, and resource allocation. Understanding combinatorial optimization is essential for applying algorithms that can efficiently navigate complex problem spaces and ensure optimal outcomes.
Computer network topology optimization: Computer network topology optimization is the process of designing and arranging the various elements of a computer network to achieve the best performance while meeting specific constraints. This includes minimizing costs, maximizing efficiency, and ensuring reliability, all while adhering to various limitations like bandwidth, latency, and physical space. The goal is to create a network structure that effectively meets user needs and operational requirements.
Conflict-directed backjumping: Conflict-directed backjumping is a search strategy used in solving constraint satisfaction problems where, upon encountering a conflict, the algorithm jumps back to the most recent variable that is relevant to the conflict rather than simply backtracking one step. This technique enhances efficiency by avoiding unnecessary backtracking and allows the search process to focus on variables that are directly involved in the current conflict, improving the likelihood of finding a solution more quickly.
Constraint optimization: Constraint optimization is the process of finding the best solution from a set of feasible solutions that satisfy specific restrictions or constraints. This involves maximizing or minimizing an objective function while adhering to limitations on resources, variables, or conditions. The goal is to achieve the optimal outcome while balancing competing requirements.
Constraint propagation techniques: Constraint propagation techniques are methods used in constraint optimization problems to reduce the search space by systematically eliminating values that cannot satisfy the constraints. These techniques help in tightening the bounds of variables, which leads to more efficient problem-solving as they allow for quicker identification of feasible solutions. By applying these methods, one can streamline the process of finding optimal solutions while ensuring that all constraints are respected.
Constraint satisfaction problems (CSPs): Constraint satisfaction problems (CSPs) are mathematical problems defined by a set of variables, each associated with a domain of values, and a set of constraints that restrict the values the variables can simultaneously take. These problems focus on finding an assignment of values to variables that satisfies all constraints. CSPs are pivotal in optimization as they represent many real-world situations where solutions must meet specific requirements, leading to further developments in constraint optimization problems that aim to not just satisfy constraints but also optimize some objective function.
Constraints: Constraints are limitations or conditions that must be satisfied in an optimization problem, defining the feasible region within which solutions can be considered. They ensure that any solution not only aims to optimize the objective function but also adheres to specific restrictions imposed by the problem's context. Understanding constraints is crucial as they directly influence the feasibility and optimality of potential solutions across various mathematical formulations.
Continuous Variables: Continuous variables are types of variables that can take on any value within a given range, making them essential in mathematical modeling and optimization problems. Unlike discrete variables that can only assume specific values, continuous variables are used to represent quantities that can be divided infinitely, such as weight, height, or time. They play a crucial role in formulating optimization problems, particularly in methods like branch and cut and in constraint optimization problems.
Convex Objective Functions: Convex objective functions are mathematical functions where the line segment between any two points on the graph of the function lies above or on the graph itself. This property ensures that any local minimum of the function is also a global minimum, making optimization problems involving convex functions particularly manageable and reliable. In the context of constraint optimization problems, understanding convexity is essential because it influences the feasibility and optimality of solutions within given constraints.
Cplex Solver: Cplex Solver is a powerful optimization software developed by IBM, designed to solve linear programming, mixed integer programming, and quadratic programming problems. It uses advanced algorithms to efficiently find the best solution to complex mathematical models that arise in constraint optimization scenarios, helping decision-makers optimize resource allocation, production scheduling, and logistics management.
Cutting Plane Methods: Cutting plane methods are optimization techniques used to solve integer and mixed-integer programming problems by iteratively refining a feasible region in order to find the optimal solution. These methods involve adding linear inequalities, or 'cutting planes,' to exclude infeasible solutions while maintaining all feasible ones, effectively tightening the bounds of the solution space. By combining cutting planes with other techniques, such as linear programming relaxation, these methods enhance the efficiency of solving complex problems.
Decision variables: Decision variables are the fundamental elements in optimization problems that represent the choices available to decision-makers. They are the unknowns we aim to determine in order to achieve the best possible outcome while satisfying constraints. These variables can take on different values and directly influence the objective function of a mathematical model, making them critical in integer linear programming, linear programming, and constraint optimization problems.
Distributed constraint optimization techniques (ADOPT, DPOP): Distributed constraint optimization techniques, specifically ADOPT and DPOP, are methods designed to solve optimization problems in a distributed manner, where multiple agents or nodes cooperate to find a solution that satisfies certain constraints while optimizing an objective function. These techniques are particularly useful in scenarios where the problem is too complex or large for a single agent to handle effectively. They leverage communication and coordination among agents to explore the solution space efficiently and reach an optimal collective outcome.
Dual Simplex Method: The dual simplex method is an optimization algorithm used for solving linear programming problems, particularly when the primal feasibility may be violated while maintaining dual feasibility. This method is essential for efficiently finding optimal solutions in various scenarios, especially when constraints change or when re-optimizing after a perturbation. It connects deeply with other concepts in optimization, like linear programming relaxation, integer programming formulations, and constraint optimization problems.
Dynamic Programming: Dynamic programming is a method used for solving complex problems by breaking them down into simpler subproblems and storing the results of these subproblems to avoid redundant calculations. This technique is particularly useful for optimization problems, allowing for efficient solutions through a structured approach that often involves solving overlapping subproblems and utilizing optimal substructure properties.
Energy Dispatch Optimization: Energy dispatch optimization is the process of determining the most efficient way to allocate and distribute energy resources to meet demand while minimizing costs and adhering to operational constraints. This involves solving complex mathematical models that take into account various factors like generation costs, demand forecasts, and system reliability, ensuring that energy systems operate at peak efficiency.
Equality constraints: Equality constraints are conditions that require a mathematical expression to be exactly equal to a specified value within an optimization problem. These constraints play a crucial role in defining feasible regions for solutions and ensuring that certain requirements are met in problems involving resources, capacities, or specific conditions that must be satisfied.
Evolutionary algorithms for optimization problems: Evolutionary algorithms are a class of optimization techniques inspired by the process of natural selection, which iteratively improve candidate solutions to optimization problems. They operate on a population of potential solutions and apply mechanisms such as selection, crossover, and mutation to evolve better solutions over successive generations. These algorithms are particularly useful for solving complex constraint optimization problems where traditional methods may struggle due to non-linearity or multiple local optima.
Feasible Region: The feasible region is the set of all possible solutions to an optimization problem that satisfy all given constraints. This region is often visualized as a geometric area in which every point represents a potential solution that meets the criteria outlined by the constraints, making it essential for finding optimal solutions in various optimization techniques.
FICO Xpress Solver: FICO Xpress Solver is a powerful optimization tool designed to solve complex mathematical problems related to constraint optimization. It uses advanced algorithms to help users find the best solutions for resource allocation, scheduling, and other decision-making processes. This solver is particularly useful in scenarios where there are numerous constraints and objectives that must be balanced to achieve optimal results.
Forward Checking: Forward checking is a constraint satisfaction technique used in solving constraint optimization problems, where it helps to prevent the search process from exploring paths that are guaranteed to fail. This method involves checking the consistency of remaining variables in the constraint graph after assigning a value to a variable, effectively reducing the search space. By identifying and eliminating inconsistent variable assignments early, forward checking can improve the efficiency of finding a solution.
Forward checking: Forward checking is a constraint satisfaction technique used during search algorithms to prevent the exploration of invalid solutions by checking constraints against future variable assignments. When a variable is assigned a value, forward checking immediately removes values from the domains of unassigned variables that are inconsistent with this assignment. This helps in detecting potential conflicts early in the search process, enhancing efficiency and reducing the overall computational effort required to find a solution.
GAMS (General Algebraic Modeling System): GAMS is a high-level modeling system designed for mathematical programming and optimization problems. It allows users to formulate complex optimization models in a structured way, making it particularly useful for constraint optimization problems where multiple conditions must be met. With GAMS, users can define variables, equations, and constraints clearly, enabling efficient problem-solving and analysis.
Generalized arc consistency (gac): Generalized arc consistency (GAC) is a concept in constraint satisfaction problems that extends the idea of arc consistency to ensure that every value in a variable's domain can be part of a solution for all related variables. This means that for each value of a variable, there is some consistent assignment of values to the other variables that satisfies the constraints of the problem. GAC is crucial in constraint optimization as it helps eliminate values that cannot be part of any valid solution, leading to a more efficient search for optimal solutions.
Global constraints: Global constraints are specific types of constraints that impose restrictions on multiple variables within a problem, capturing complex relationships in a single expression. They enhance the efficiency of solving problems by allowing constraint solvers to recognize and handle these relationships directly, rather than treating each variable's restrictions independently. This can lead to a more streamlined solution process in various optimization and satisfaction scenarios.
Global Optimization Techniques: Global optimization techniques are methods used to find the best solution or maximum/minimum value for a given objective function across all possible solutions, rather than just a local optimum. These techniques are essential when dealing with complex problems where the solution space has multiple peaks and valleys, allowing for a comprehensive search that avoids getting stuck in suboptimal solutions. They are particularly valuable in scenarios where constraints limit the feasible solutions, ensuring that the optimal solution adheres to specific requirements.
Greedy algorithms: Greedy algorithms are a type of algorithmic approach that builds up a solution piece by piece, always choosing the next piece that offers the most immediate benefit. This approach is often used to solve optimization problems where a locally optimal choice at each step is believed to lead to a globally optimal solution. Greedy algorithms are especially useful in problems involving combinatorial structures, and their computational complexity can vary significantly based on the specific problem being addressed.
Gurobi Solver: Gurobi Solver is a powerful optimization software used for solving various types of mathematical programming problems, including linear programming, mixed-integer programming, and quadratic programming. It is particularly recognized for its speed and efficiency in handling large-scale constraint optimization problems, making it a popular choice among researchers and practitioners in fields like operations research, finance, and logistics.
Hard Constraints: Hard constraints are strict limitations in optimization problems that must be satisfied for a solution to be considered valid. These constraints define the boundaries within which a feasible solution can exist, ensuring that certain criteria or requirements are met, such as capacity limits, resource availability, and specific conditions that cannot be violated.
Heuristic methods: Heuristic methods are problem-solving approaches that use practical techniques or shortcuts to produce solutions that may not be optimal but are sufficient for reaching immediate goals. They are particularly useful in complex optimization problems where finding the exact solution is computationally infeasible. These methods often prioritize speed and simplicity over accuracy, making them valuable tools in scenarios like constraint optimization where finding a feasible solution quickly is crucial.
Hill climbing algorithm: A hill climbing algorithm is a mathematical optimization technique that incrementally improves a solution by making small changes and selecting the best neighboring solution. It operates on the principle of local search, seeking to find the peak of a landscape that represents optimal solutions to a given problem, often used in the context of constraint optimization problems. The algorithm evaluates neighboring configurations and moves towards higher values, effectively navigating through the search space until it finds a local maximum or cannot improve further.
Inequality constraints: Inequality constraints are mathematical expressions that impose restrictions on the possible values of decision variables in optimization problems, typically represented as inequalities. These constraints define a feasible region within which optimal solutions can be sought, affecting how problems are formulated and solved. In various optimization techniques, these constraints help in narrowing down the solution space to feasible solutions that satisfy given conditions.
Integer variables: Integer variables are variables that can only take on whole number values, meaning they cannot be fractions or decimals. In the context of optimization problems, especially constraint optimization problems, these variables play a crucial role in ensuring that the solutions are feasible and applicable to real-world scenarios where quantities must be whole numbers, such as in resource allocation, scheduling, and logistics.
Job shop scheduling: Job shop scheduling is the process of organizing and allocating resources to complete a set of tasks or jobs in a manufacturing or production environment. This involves determining the optimal order and timing for each job on various machines to minimize completion time, maximize resource utilization, and meet delivery deadlines. The complexity of this scheduling problem often leads to significant challenges in efficiency and effectiveness, connecting it to concepts like computational difficulty, competitive algorithms, and optimization under constraints.
Jump Modeling Language for Julia: The Jump Modeling Language for Julia is a high-level modeling language designed for formulating and solving optimization problems, particularly those related to mathematical programming. It provides a flexible and expressive way to define constraints, variables, and objective functions in a clear manner, making it especially useful for constraint optimization problems where the aim is to find the best solution under specific restrictions.
Least constraining value: The least constraining value is a strategy used in constraint optimization problems that focuses on selecting values for variables in a way that imposes the fewest restrictions on the remaining variables. This approach helps maintain flexibility in the search space, allowing for more potential solutions as it prioritizes options that do not overly limit subsequent choices. It plays a critical role in ensuring that the overall problem-solving process remains efficient and effective.
Linear Objective Functions: Linear objective functions are mathematical expressions that represent a goal to be maximized or minimized, expressed as a linear combination of decision variables. These functions are crucial in optimization problems, particularly where constraints exist, as they provide a straightforward way to quantify outcomes based on various choices. The simplicity and directness of linear functions make them essential for identifying optimal solutions under given restrictions.
Linear Programming (LP): Linear programming is a mathematical method used for optimizing a linear objective function, subject to a set of linear equality and inequality constraints. It aims to find the best outcome in a mathematical model whose requirements are represented by linear relationships. This technique is essential in constraint optimization problems, where the goal is to maximize or minimize a particular quantity while adhering to certain limitations.
Logical constraints: Logical constraints are conditions that restrict the possible values of decision variables in optimization problems based on logical relationships. These constraints allow for the formulation of complex decision-making scenarios by capturing relationships that can be expressed as true or false, often using logical operators such as AND, OR, and NOT. They are essential in representing real-world situations where decisions depend on the fulfillment of certain criteria.
Mathematica Software: Mathematica is a computational software system used for symbolic and numerical calculations, data visualization, and programming. It provides powerful tools for solving complex mathematical problems, including constraint optimization problems, by allowing users to model, analyze, and visualize data efficiently.
Max-sum algorithm: The max-sum algorithm is a message-passing algorithm used in distributed systems to solve optimization problems, particularly in the context of constraint optimization problems. It operates by exchanging messages between nodes in a network to collectively compute the maximum value of a given objective function while satisfying specified constraints. This algorithm is effective for applications where decision variables are distributed across multiple agents or nodes, allowing for decentralized computation.
Metaheuristics: Metaheuristics are high-level strategies designed to guide other heuristics toward the exploration of large search spaces for optimization problems. These methods help to find good enough solutions within a reasonable time frame, especially when traditional optimization techniques are inefficient. They often incorporate mechanisms to escape local optima, allowing for more robust search processes and applications across various complex problems, such as combinatorial optimization, constraint satisfaction, and more.
Minimum Remaining Values (MRV): Minimum Remaining Values (MRV) is a heuristic used in constraint optimization problems to determine the most constrained variable by identifying the variable with the fewest legal values left. This strategy helps in efficiently solving problems by prioritizing variables that are more difficult to assign values to, reducing the search space and potentially leading to faster solutions. By focusing on these constrained variables, it can help avoid dead ends in the search process.
Minizinc modeling language for optimization problems: MiniZinc is a high-level, declarative modeling language specifically designed for formulating constraint optimization problems. It allows users to express complex constraints and objectives in a clear and concise manner, making it easier to model various optimization scenarios, such as scheduling, resource allocation, and network design. MiniZinc works with various back-end solvers that can efficiently process these models to find optimal solutions.
Multi-objective constraint optimization techniques: Multi-objective constraint optimization techniques are methods used to optimize problems that involve multiple objectives while satisfying a set of constraints. These techniques aim to find the best trade-offs between conflicting objectives, ensuring that all constraints are adhered to, which is crucial in real-world scenarios where solutions must balance different criteria such as cost, time, and quality.
Multi-objective functions: Multi-objective functions are mathematical expressions that involve two or more objectives that need to be optimized simultaneously, often subject to certain constraints. These functions are essential in scenarios where decisions need to be made considering various competing criteria, leading to trade-offs among them. They are particularly relevant when dealing with complex problems where no single solution can satisfy all objectives perfectly, resulting in a set of optimal solutions known as Pareto optimal solutions.
Non-convex objective functions: Non-convex objective functions are mathematical functions that do not satisfy the property of convexity, meaning that there are multiple local minima and maxima. This complexity can lead to challenges in optimization problems, particularly in finding the global optimum, as traditional techniques that work for convex functions may not be effective here. In the context of constraint optimization problems, these functions can complicate the search for feasible solutions due to their unpredictable behavior and the presence of multiple feasible regions.
Nonlinear objective functions: Nonlinear objective functions are mathematical expressions that involve at least one variable raised to a power other than one or that include variables multiplied together. These functions are essential in optimization problems where the relationship between decision variables is not linear, leading to more complex behavior and solutions. Understanding how these functions behave helps in finding optimal solutions under constraints.
Objective Function: An objective function is a mathematical expression that defines the goal of an optimization problem, representing what needs to be maximized or minimized based on certain constraints. The formulation of the objective function plays a critical role in guiding algorithms and techniques to find optimal solutions across various contexts, impacting how decisions are made and resources are allocated effectively.
OptaPlanner Framework: The OptaPlanner Framework is an open-source constraint solver that optimizes planning and scheduling problems by finding the best solutions while adhering to various constraints. It is designed to help organizations make better decisions and improve resource allocation by efficiently solving complex constraint optimization problems, enabling businesses to maximize efficiency and minimize costs.
Or-tools by Google: or-tools by Google is an open-source software suite for solving combinatorial optimization problems, which focuses on enabling efficient and effective decision-making through the use of algorithms and modeling tools. It provides a range of functionalities including linear programming, constraint programming, and routing optimization. This makes it a powerful resource for tackling complex real-world problems where multiple constraints need to be satisfied.
Pareto Optimality Concept: The Pareto Optimality Concept is an economic principle that defines a situation where resources are allocated in the most efficient manner, such that no individual can be made better off without making someone else worse off. This concept plays a crucial role in understanding constraint optimization problems as it highlights the trade-offs and competing objectives involved in optimizing multiple outcomes simultaneously.
Portfolio Optimization: Portfolio optimization is the process of selecting the best mix of assets to achieve a specific investment goal while minimizing risk. This concept is crucial in finance, as it involves balancing expected returns against the inherent risks associated with different investment options. By using various mathematical and statistical techniques, investors can determine the optimal allocation of resources among various assets, which can be greatly informed by methods like dynamic programming and approaches to constraint optimization problems.
Precedence Constraints: Precedence constraints are rules that dictate the order in which tasks or activities must be performed in a project or optimization problem. These constraints ensure that certain tasks cannot start until others have been completed, making them critical for planning and scheduling in constraint optimization problems. They play a vital role in determining feasible solutions by impacting timelines and resource allocation.
Problem Formulation: Problem formulation is the process of defining a problem in a structured way, identifying the objectives, constraints, and decision variables involved. It serves as the foundation for solving optimization problems by translating real-world scenarios into mathematical models, allowing for systematic analysis and solution development.
Project scheduling with resource constraints (RCPSP): Project scheduling with resource constraints (RCPSP) is a combinatorial optimization problem that involves scheduling a set of activities within a project while adhering to limited resources. This method ensures that all tasks are completed within a specific timeframe, considering the availability and constraints of various resources such as manpower, equipment, and materials. By optimizing the scheduling process, RCPSP aims to minimize project duration or maximize the use of available resources.
Pulp python library: The PuLP Python library is a tool used for formulating and solving linear programming and mixed-integer programming problems in Python. It provides a user-friendly interface for defining optimization problems, adding constraints, and accessing various solvers to find optimal solutions. This library is especially useful for handling constraint optimization problems, allowing users to model real-world scenarios involving limited resources and specific requirements.
Pyomo modeling capabilities: Pyomo modeling capabilities refer to the features and tools offered by the Pyomo library for defining and solving optimization problems in Python. This includes the ability to formulate complex mathematical models, handle constraints, and integrate various solvers, making it a versatile choice for constraint optimization problems. With Pyomo, users can easily represent decision variables, objective functions, and constraints in a way that is intuitive and manageable for a variety of applications.
Resource constraints: Resource constraints refer to the limitations imposed on the availability of resources needed to achieve a specific goal or complete a task. In optimization problems, these constraints restrict the possible solutions by defining the boundaries within which resources must be allocated, ensuring that no resource is overused or wasted. Understanding resource constraints is crucial for efficiently solving optimization problems where balancing multiple competing needs is essential.
Scheduling problems: Scheduling problems involve assigning resources to tasks over time in an efficient manner, ensuring that constraints and objectives are met. These problems are critical in various fields such as manufacturing, transportation, and project management, as they help determine optimal timelines and resource allocations. By focusing on optimizing task sequences, minimizing delays, and reducing costs, scheduling problems can significantly impact overall productivity and resource utilization.
SCIP Software for Constraint Integer Programs: SCIP (Solving Constraint Integer Programs) is a software framework designed for solving constraint integer programming problems. It combines the techniques of constraint programming and mixed-integer programming to handle complex combinatorial problems efficiently, allowing users to model and solve various optimization tasks effectively. SCIP is widely used in both academic research and practical applications due to its powerful algorithms and flexibility in handling different problem types.
Simplex method: The simplex method is an algorithm used for solving linear programming problems by optimizing a linear objective function subject to linear equality and inequality constraints. It systematically examines the vertices of the feasible region defined by these constraints to find the optimal solution, providing insights into how resource allocation can be maximized or minimized effectively. This method is especially significant in applications where decision-making involves limited resources and competing objectives.
Simulated Annealing: Simulated annealing is an optimization technique inspired by the annealing process in metallurgy, where controlled cooling of materials leads to a more stable structure. This method allows for exploring the solution space of optimization problems by probabilistically accepting worse solutions in order to escape local optima, aiming for a global optimum. Its flexibility makes it applicable across various domains, integrating aspects of local search techniques and heuristics, while also being relevant in constraint optimization problems.
Social network influence maximization: Social network influence maximization is the process of identifying and selecting a subset of individuals within a social network to maximize the spread of information, behaviors, or influences among its members. This concept is crucial in understanding how information cascades through social networks, and it has applications in marketing, public health, and viral campaigns.
Soft constraints: Soft constraints are conditions or preferences in a problem that are desirable but not mandatory for a solution. Unlike hard constraints, which must be strictly adhered to, soft constraints allow for flexibility and can be violated if necessary to find an optimal or feasible solution. This characteristic is crucial in various scenarios, as it helps in balancing conflicting requirements and achieving more satisfactory outcomes in complex problems.
Solution Space: The solution space refers to the set of all possible solutions to a given optimization problem, defined by the constraints and objectives of that problem. This concept is essential as it helps to visualize and understand the range of potential solutions available, guiding methods used to find the optimal solution. Analyzing the solution space aids in determining feasibility, boundedness, and the nature of the solutions within various mathematical frameworks.
Standard form of LP: The standard form of linear programming (LP) is a mathematical representation of an optimization problem where the objective function is maximized or minimized subject to a set of linear equality constraints and non-negativity restrictions on the variables. This format is essential for applying various solution methods, including the Simplex algorithm, as it provides a clear structure for analyzing feasible solutions and optimality conditions.
Supply chain network design: Supply chain network design is the process of strategically planning the layout and structure of a supply chain to optimize operations, reduce costs, and enhance service levels. It involves determining the locations of facilities, distribution centers, and transportation routes while considering various constraints such as demand, capacity, and transportation costs to ensure a smooth flow of goods from suppliers to customers.
Supply chain optimization: Supply chain optimization is the process of enhancing the efficiency and effectiveness of a supply chain to minimize costs while maximizing service levels. This involves improving the flow of goods, information, and finances across various stakeholders to ensure that products are delivered in the right quantity, to the right place, and at the right time. It incorporates mathematical and computational techniques to solve complex logistical challenges, often utilizing methodologies that focus on cost minimization, resource allocation, and constraint management.
Tabu search: Tabu search is a metaheuristic optimization technique that guides a local search procedure to explore the solution space beyond local optimality by using memory structures that describe previously visited solutions. This technique is particularly effective in avoiding cycles and getting stuck in local optima by prohibiting moves that revert to recently explored solutions, thus enhancing the ability to find global optima. It blends local search strategies with memory mechanisms to handle complex problems effectively.
Telecommunications network design: Telecommunications network design is the process of planning and creating a structured layout for communication networks that facilitate the transmission of data, voice, and video across various mediums. This involves selecting the right technologies, establishing protocols, and optimizing resources to ensure reliable and efficient connectivity. The design process also considers constraints like budget, bandwidth requirements, and regulatory compliance, making it a key area in constraint optimization problems.
Timetabling Problems: Timetabling problems involve the allocation of resources, such as time slots and locations, to events in a way that satisfies a set of constraints. These problems are typically found in contexts like education, transportation, and workforce scheduling, where multiple activities must be organized simultaneously while considering various restrictions like availability and conflicts.
Transportation network optimization: Transportation network optimization is the process of improving the efficiency and effectiveness of transportation systems, ensuring that resources are allocated in a way that minimizes costs and maximizes performance. This involves the use of mathematical models and algorithms to find the best routes for transporting goods or people while considering constraints like capacity, demand, and operational limitations.
Variable Neighborhood Search: Variable Neighborhood Search is a metaheuristic optimization technique that systematically explores the solution space by changing the neighborhood structures within the search process. This method helps escape local optima by diversifying the search, allowing it to examine different areas of the solution space through a series of neighborhood changes. By integrating multiple neighborhood structures, it enhances the likelihood of finding a global optimum, making it especially useful in local search techniques and constraint optimization problems.
Weighted sum method for multi-objective optimization: The weighted sum method for multi-objective optimization is a technique used to convert multiple objectives into a single objective by assigning weights to each objective and summing them. This method simplifies the process of finding a solution by allowing decision-makers to prioritize objectives according to their importance, thus facilitating a more straightforward optimization problem. By adjusting the weights, one can explore different trade-offs between conflicting objectives and identify a range of possible solutions.
Workforce scheduling: Workforce scheduling is the process of assigning work tasks and shifts to employees in a way that meets business demands while considering employee availability, skills, and labor laws. This optimization involves creating a timetable that ensures adequate staffing levels for operations while minimizing labor costs and maximizing employee satisfaction. Effective workforce scheduling is crucial in industries where demand fluctuates, and it can be modeled as a constraint optimization problem to find the best possible schedule under specific restrictions.
ε-constraint method for multi-objective optimization: The ε-constraint method is a technique used in multi-objective optimization to convert a multi-objective problem into a single-objective problem by treating all but one of the objectives as constraints. This method helps in finding Pareto optimal solutions by setting thresholds (ε values) for the other objectives, which allows for a more systematic exploration of the trade-offs between conflicting objectives. By varying these constraints, decision-makers can identify various solutions that represent different trade-offs among objectives.
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
Back
Practice QuizGlossary
Practice QuizGlossary
Next guide